The angle of twist is the angle through which a cross-section of a shaft rotates around its center line due to an applied torque. Understanding this parameter is important in predicting the performance of shaft components under load and ensuring their safe and reliable operation.

In this article, we define the angle of twist, its formula, and the factors affecting it.
What is Angle of Twist?
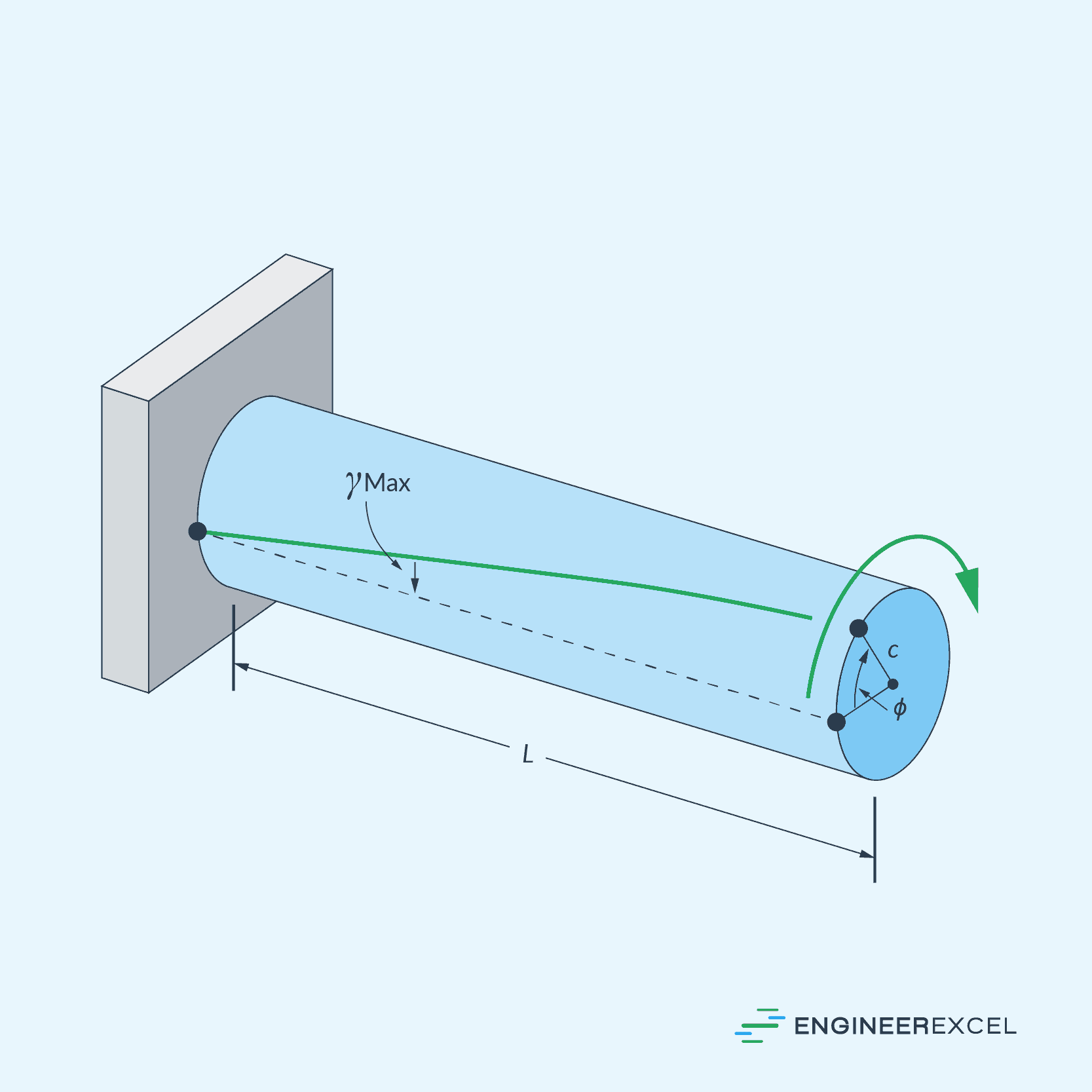
When torque is applied to a shaft, it causes the shaft to twist about its longitudinal axis. If the shaft is fixed at one end and torque is applied to the other end, the shaft will distort into a skewed shape, causing the shaft’s cross-section to rotate through an angle. This angle is known as the angle of twist.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
The angle of twist refers to the angle through which a cross-section of a shaft rotates around its center line due to an applied torque. This angle varies along the length of the shaft and increases as the distance from the fixed end increases.
The design of a shaft normally requires limiting the amount of rotation or twisting that can occur when the shaft is exposed to torque. Hence, understanding the angle of twist allows engineers to predict the performance of shaft components under load and ensure their safe and reliable operation. This is particularly important in engineering applications involving axles or drive shafts for vehicles and machinery.
Factors Influencing the Angle of Twist
There are several factors that influence the angle of twist in a shaft. These include the properties of the shaft material, shaft geometry and dimensions, and magnitude of the applied torque.
Material Properties
The properties of the material used for the shaft have a significant impact on the angle of twist. One crucial property is the shear modulus, which represents the material’s resistance to shear deformation. Materials with a higher shear modulus are less likely to twist under a given torque.
The table below shows some common shaft materials and their shear moduli:
| Material | Shear Modulus (GPa) |
|---|---|
| Steel | 75-85 |
| Brass | 35-45 |
| Aluminum | 25-30 |
| Titanium | 40-50 |
Besides the shear modulus, the material’s yield strength must also be considered since it determines the maximum torque a shaft can handle before permanent deformation occurs.
Shaft Dimensions
The dimensions of the shaft, such as length and diameter, directly influence the angle of twist. A longer shaft will experience a greater angle of twist under the same torque when compared to a shorter shaft.
Additionally, the shaft’s cross-sectional shape also affects the angle of twist. Common shaft shapes include solid circular, hollow circular, and rectangular cross-sections.
Generally, a shaft with a larger diameter or cross-sectional area will experience a smaller angle of twist under the same torque. As the diameter increases, the shaft becomes more resistant to torsion. On the other hand, minimizing the shaft diameter may result in increased twist and potential failure under specific loads.
Applied Torque
Lastly, the applied torque has a significant influence on the angle of twist experienced by a shaft. Greater torque leads to a larger angle of twist, resulting in more shear stress and potential deformation. When the applied torque exceeds the material’s yield strength or the shaft’s torsional stiffness, it may cause the shaft to fail.
Angle of Twist Formula
The angle of twist can be calculated using the following formula:
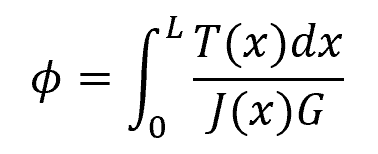
Where:
- φ = the angle of twist of one end of the shaft with respect to the other end [radians]
- T(x) = the internal torque at the arbitrary position x [N-m]
- J = the shaft’s polar moment of inertia expressed as a function of position x [m4]
- L = length of the shaft [m]
- G = shear modulus of the shaft material [Pa]
For a constant torque and constant cross-sectional area, the above equation can be simplified as follows:
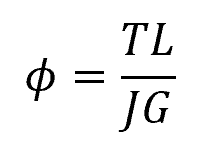
For a solid circular shaft, the polar moment of inertia can be calculated using the formula:

Where:
- D = diameter of the shaft [m]
If the shaft is hollow, then the polar moment of inertia becomes:
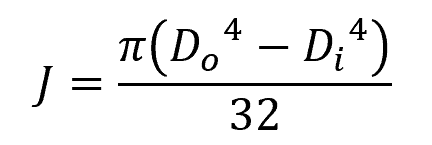
Where:
- Do = outer diameter of the shaft [m]
- Di = inner diameter of the shaft [m]
In cases where the shaft is subjected to multiple torques, the net angle of twist is calculated by superimposing the angles of twist due to each individual torque. If torque is constant along the shaft, the above formula can be simply summed. However, if torque varies with the length of the shaft, integration is needed to accurately calculate the angle of twist.
It is important to note that the angle of twist increases linearly with the shaft length and applied torque for elastic deformation. This relationship remains valid until the material reaches its elastic limit, after which the shaft may suffer permanent deformation or even failure.
Example Problem
Problem Statement: A solid circular shaft with a length of 2 meters, diameter of 0.1 meters, and shear modulus of 80 GPa is subjected to a torque of 1500 Nm. Calculate the angle of twist at the end of the shaft.
Answer: We can use the angle of twist formula:
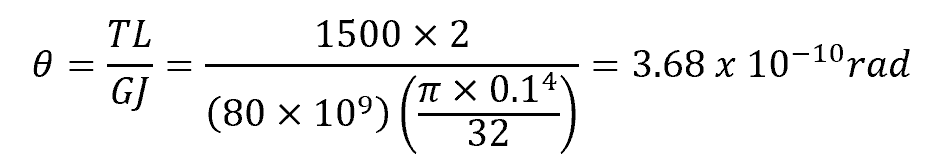
So, the angle of twist at the end of the shaft is approximately 4.97 × 10^-4 radians.
