Stagnation pressure refers to the static pressure at a stagnation point in a fluid flow, where the fluid velocity is zero. This pressure is what the fluid would experience if it were brought to rest without any loss of mechanical energy.

In this article, we will discuss the concept of stagnation pressure in incompressible and compressible flows, along with its measurement techniques and applications.
What is Stagnation Pressure
Stagnation pressure, also known as total pressure, represents the pressure a fluid exerts when it is brought to a complete stop, isentropically, from a given state of motion. Consider a moving fluid at a given velocity, pressure, and density. If this fluid is decelerated isentropically—without any entropy change or heat transfer—to a zero-velocity state known as the stagnation point, the resulting pressure is its stagnation pressure.
This pressure represents the highest value encountered within the flow field. It is the combined result of the static pressure and the dynamic pressure measured at a considerable distance upstream.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
It is important to highlight that the stagnation pressure is a theoretical construct useful for understanding flowing systems, rather than a pressure one would directly measure in a stationary fluid. Under the assumption that no energy losses occur during the flow process (isentropic conditions), the stagnation pressure is typically higher than the static pressure of the moving fluid due to the conversion of kinetic energy into pressure energy.
Stagnation Pressure in Incompressible Flow
Incompressible flow implies that the density of the fluid remains constant. For such flows, Bernoulli’s equation provides a relationship between the stagnation pressure, static pressure, and dynamic pressure as follows:

Where:
- po = stagnation pressure [Pa]
- p = static pressure [Pa]
- ρ = fluid density [kg/m3]
- V = fluid velocity [m/s]
As shown in the above equation, the stagnation pressure is raised above the static pressure by an amount called the dynamic pressure, which is due to fluid motion. It is important to note that this equation is only valid along a streamline and for flows without frictional losses.
Stagnation Pressure in Compressible Flow
Compressible flow implies that the density of the fluid changes with variations in pressure and temperature. Hence, the above equation requires corrections for changes in density. In this case, the stagnation pressure can be computed by utilizing the isentropic relations, as shown in the following equation:
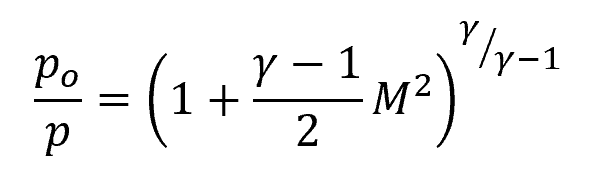
Where:
- γ = adiabatic index [unitless]
- M = Mach number [unitless]
In the above equation, the adiabatic index, also known as the specific heat ratio, represents the ratio of the specific heat at constant pressure to the specific heat at constant volume. On the other hand, the Mach number represents the ratio of the local flow velocity to the speed of sound in the medium.
If the stagnation temperature is known, it can also be related to the stagnation temperature using the following equation:
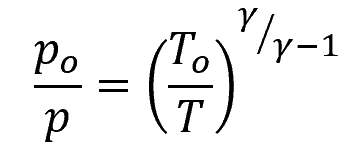
Where:
- To = stagnation temperature [K]
- T = static temperature [K]
Measurement Techniques
In measuring stagnation pressure within a flow, engineers primarily employ two critical instruments: the Pitot-Static Tube and Pressure Transducers.
Pitot-Static Tube
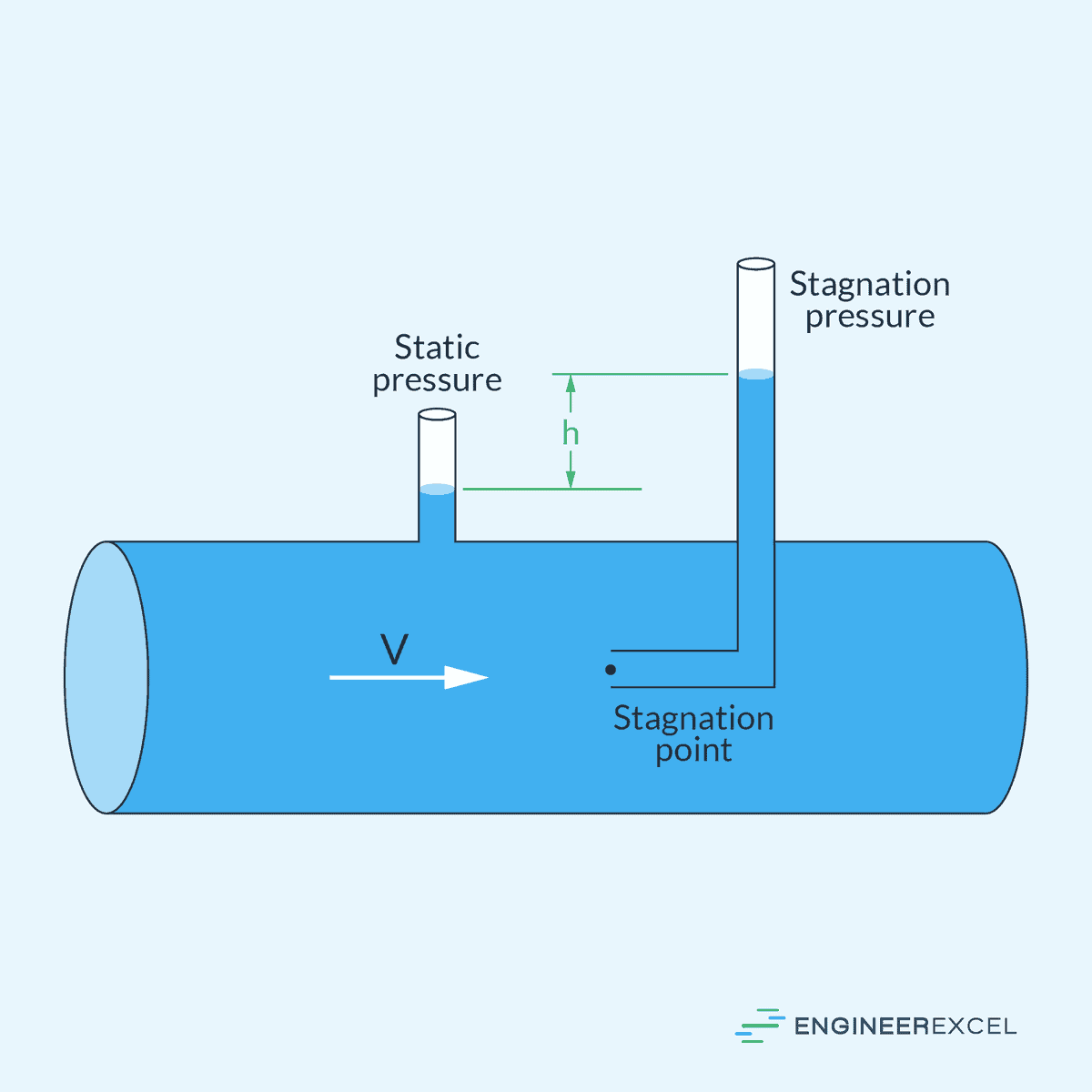
A Pitot-Static Tube is an instrument that consists of two concentric tubes; the inner tube measures the stagnation pressure, while the outer tube has ports to sense the static pressure. When placed in a fluid flow, the difference in pressures can be used to calculate the flow’s velocity using Bernoulli’s principle.
Pressure Transducers
Pressure Transducers convert pressure into an electrical signal and can be used to measure stagnation pressure in a variety of environments. They are particularly suitable for situations requiring high accuracy and a fast response time. Pressure transducers often consist of a diaphragm and a pressure-sensitive element that responds to changes in stagnation pressure, creating an electrical signal that can be read and interpreted.
Applications
The concept of stagnation pressure is relevant to the fields of aerodynamics, wind tunnel testing, and jet engine design.
Aerodynamics
In aerodynamics, engineers calculate the stagnation pressure at various points on an aircraft’s surface to evaluate the local airspeed and the lift generated by the wings. The difference in pressure between the stagnation point and other points on the wing aids in the estimation of lift coefficients, which are essential for safe and efficient aircraft design.
Wind Tunnel Testing
Wind tunnel testing utilizes stagnation pressure measurements to simulate real flight conditions for scale models. By measuring the stagnation pressure in a wind tunnel, engineers can infer the dynamic pressure, and thereby the Mach number, to ensure similarities between the test conditions and the actual conditions the prototype will encounter.

Understanding the stagnation pressure distribution helps to identify potential issues with aerodynamic drag and lift that can then be addressed in the design stage.
Jet Engine Design
In jet engine design, the engine’s compressor blades are shaped and arranged to maximize pressure recovery, which involves bringing the incoming airflow to a stop as efficiently as possible, thus maximizing the stagnation pressure. Engineers study the pressure recovery to optimize thrust and fuel efficiency. The stagnation pressure within the combustion chamber, as well, has a direct impact on the engine’s overall thrust, with a higher stagnation pressure generally leading to improved performance.
