The Bernoulli equation describes the conservation of energy for a fluid flowing in a steady, incompressible stream. It states that the sum of the pressure energy, kinetic energy, and potential energy per unit volume of the fluid remains constant along any streamline.

In this article, we will discuss the Bernoulli Equation in detail, including its assumptions, applications, and limitations in different flow scenarios.
Understanding the Bernoulli Equation
The Bernoulli equation is a fundamental theorem in fluid dynamics that establishes the relationship between the pressure, velocity, and elevation within a moving fluid. The equation was vaguely stated in words in 1738 in a textbook by Daniel Bernoulli, and a complete derivation of the equation was given in 1755 by Leonhard Euler.
The Bernoulli equation essentially states that an increase in the speed of the fluid occurs simultaneously with a decrease in pressure or a decrease in the fluid’s potential energy, as shown in the following equation:

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.

Where:
- p = pressure energy per unit volume [Pa]
- ρ = density of the fluid [kg/m3]
- V = velocity of the fluid [m/s]
- g = acceleration due to gravity [9.81 m/s2]
- h = elevation head above a reference point [m]
Fluid movement correlates with this equation; high-velocity flow areas have reduced pressure, while lower velocity areas have higher pressure.
Assumptions of the Bernoulli Equation
Bernoulli’s Equation is not universally applicable. Hence, it is important to understand the underlying assumptions in order to apply it accurately in fluid flow analysis.
Frictionless Flow
One of the key assumptions of the Bernoulli equation is that the flow is frictionless. This means that the equation assumes the absence of viscous forces or any form of internal friction within the fluid.
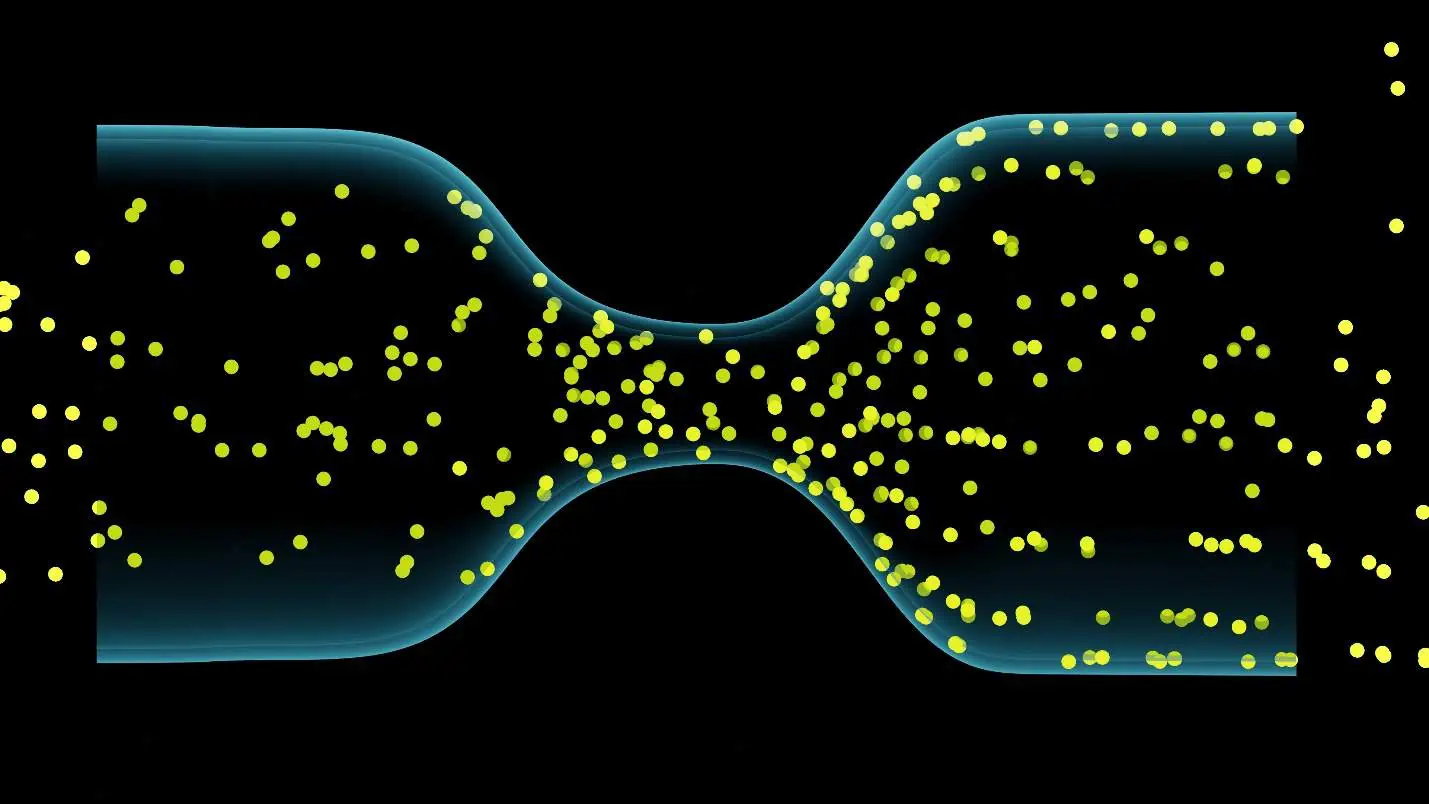
In reality, however, fluids often exhibit viscosity, leading to shear stress and energy dissipation in the form of heat. Before applying the Bernoulli equation, make sure that the impact of friction is negligible.
Incompressible Flow
Another assumption is that the flow is incompressible. This means that the density of the fluid remains constant throughout. This is generally accurate for liquids, but gases only meet this criterion under low-velocity conditions where density variations are negligible.
Steady Flow
Steady flow implies that the fluid properties at any given point in the flow field do not change over time. This assumption is essential for the Bernoulli equation because it relies on a constant energy principle along a streamline.
One-Dimensional Flow
Finally, the assumption of one-dimensional flow allows for the simplification of the fluid’s motion to variations along a single dimension. This means that the equation is applied along a streamline and normal effects are not considered.
Applications of Bernoulli Equation
Fluid Flow Measurement
The Bernoulli equation is used in fluid dynamics for measuring flow rates. Devices like the Venturi meter utilize pressure differences, a principle explained through the Bernoulli equation, to calculate flow velocity.
Airfoil Lift
Aeronautical engineers use the Bernoulli equation to describe aircraft wing lift. Airfoil-shaped wings generate lift by creating a pressure differential between the upper and lower surfaces. The equation aids in predicting how changes in velocity impact pressure, which contributes to the lift force acting on the wing.
Piping Systems
In piping systems, the Bernoulli equation helps in predicting the behavior of fluids in motion, notably the relationship between pressure losses due to elevation changes and friction. It is crucial for designing efficient systems that move liquids and gases through pipes, such as in water distribution networks or industrial process piping.
Cardiovascular Analysis
In medical fields, the Bernoulli equation assists in cardiovascular diagnostics by estimating blood flow velocities and pressure differences across heart valves. This application is integral in non-invasive techniques like echocardiography, improving patient diagnoses and treatments.
Limitations of the Bernoulli Equation
To illustrate the limitations of the Bernoulli equation, consider the diagram below showing the regions of
validity and invalidity of the Bernoulli equation in a tunnel model (a), a propeller (b), and a chimney (c).

For instance, when analyzing the flow over an object in a wind tunnel, the equation is applicable primarily within the core flow. The regions close to the walls and the object’s surface experience boundary layer effects, characterized by velocity gradients and energy dissipation, which are not considered by Bernoulli’s formula. Additionally, downstream of the object, the wake region, exhibiting complex turbulent behavior, also lies outside the scope of the equation.
In the case of flows involving propellers, differences in energy states must be accounted for. The equation may predict flows accurately upstream and downstream of a propeller. However, near the propeller blades and in the helical vortices caused by the spinning blades, the fluid dynamics involve additional energetic interactions that the Bernoulli Equation does not capture.
Moreover, when considering flows such as through a chimney, Bernoulli’s Equation is only applicable away from heat sources. The heat addition within the fire alters the fluid’s density and, consequently, the flow characteristics. Therefore, while using Bernoulli’s principle to predict the behavior of the flow within such systems, one cannot ignore the alterations brought about by temperature changes.
Example Problem
Problem: A water pipe has a diameter of 10 cm at a certain point. The pressure at that point is 200 kPa and the velocity of the water is 4 m/s. If the pipe narrows to a diameter of 5 cm at another point, what is the pressure at that point?
Solution: Since the problem did not mention anything about the elevation of the pipe, we can neglect the elevation head. First, we need to find the velocity at the second point using the continuity equation:

Now, using Bernoulli equation, we can relate the pressure and velocity at the two points in the pipe as follows:
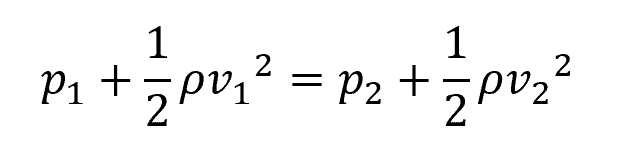
Assuming the density of water is 1000 kg/m3:
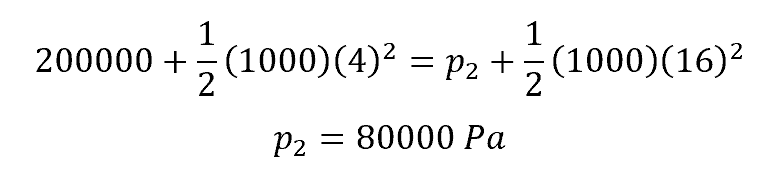
Therefore, the pressure at the second point in the pipe where the diameter narrows to 5 cm is 80 kPa.
