Dynamic pressure is a measure of the kinetic energy per unit volume of a fluid in motion. In aerodynamics and hydrodynamics, it is an essential parameter used to assess the impact of fluid flow on objects like aircraft and ships, providing insights into the forces experienced during movement.

In this article, we will look into the concept of dynamic pressure, its calculation, measurement, and the effect of compressibility on dynamic pressure.
What is Dynamic Pressure
In fluid mechanics, pressure is the force per unit area exerted by fluid molecules due to their random motion and collisions with the container boundaries. When a fluid is static and not flowing, the pressure is uniform in all directions. However, when the fluid is in motion, the measured pressure varies depending on the direction of movement, giving rise to the concept of dynamic pressure.
Dynamic pressure, also known as velocity pressure, represents the pressure quantity exerted by a fluid in motion. Specifically, it refers to the kinetic energy per unit volume of a fluid flow. It is an additive value used with static pressure to account for the total pressure within a system.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
Engineers frequently assess dynamic pressure when analyzing forces exerted on aircraft surfaces or when measuring airflow within a ventilation system.
In aerodynamics, the importance of dynamic pressure is twofold. First, it’s essential for the calculation of the airflow around airfoils, which directly impacts lift—the force that enables an aircraft to ascend or sustain flight. Second, it plays a significant role in the design of various components meant to interface with moving fluids, like compressor blades in jet engines or wind turbine blades.
Dynamic pressure also influences the speed at which objects fall through an atmosphere, known as their terminal velocity. This terminal velocity occurs when the force of dynamic pressure matches the object’s weight, resulting in zero net acceleration.
Understanding dynamic pressure is important in accurately determining the forces acting on objects in fluid environments, which can range from aircraft to automotive vehicles and even to natural phenomena such as wind effects on structures.
Dynamic Pressure Calculation
Dynamic pressure is a concept derived from Bernoulli’s principle which quantifies the kinetic energy per unit volume of a fluid in motion. It can be mathematically represented by the equation:
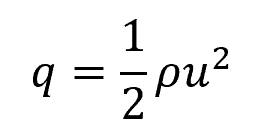
Where:
- q = dynamic pressure [Pa]
- ρ = fluid density [kg/m³]
- u = fluid velocity [m/s]
While dynamic pressure is treated as a pressure quantity in calculations, it is not actually a type of pressure. It is more accurately described as a convenient label for the quantity, which signifies the reduction in pressure caused by the fluid’s velocity.
Effect of Compressibility on Dynamic Pressure
In incompressible flows, density remains constant, allowing dynamic pressure to change solely based on velocity. However, in compressible flows, such as those encountered at high speeds or with significant pressure changes, the fluid density can vary considerably. The dynamic pressure for compressible flows, therefore, becomes a function of both velocity and the changing density.
In this case, isentropic relations can be used to define dynamic pressure as follows:
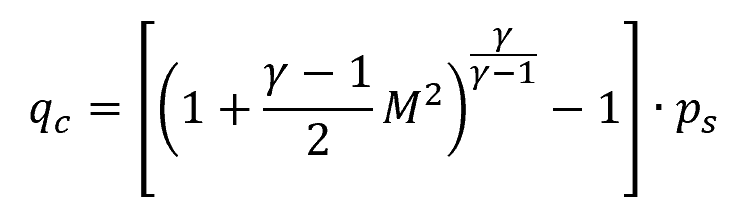
Where:
- qc = compressible dynamic pressure [Pa]
- ps = static pressure [Pa]
- M = Mach number [unitless]
- γ = adiabatic index [unitless]
The Mach number represents the ratio of an object’s speed to the speed of sound in the surrounding medium. On the other hand, the adiabatic index, also known as the ratio of specific heats, represents the ratio of the fluid’s heat capacity at constant pressure to its heat capacity at constant volume.
Measurement of Dynamic Pressure
Pitot-Static Tube
A pitot-static tube is the primary instrument for measuring the dynamic pressure in a fluid flow. It consists of two concentric tubes: the inner tube, or pitot tube, which faces the flow and measures the stagnation pressure, and the outer tube, which has side holes to measure the static pressure. The difference between these pressures, obtained using a manometer or electronic pressure transducer, yields the dynamic pressure.

It is vital to ensure that the pitot tube is aligned with the flow to avoid measurement errors caused by angular misalignment.
Pressure Transducers
Pressure transducers convert fluid pressure into an electrical signal and are often used to measure dynamic pressure due to their high accuracy and fast response times. These devices generally contain a diaphragm that deflects under the influence of fluid pressure. This deflection is then converted into an electrical output.
Calibration against known pressures is necessary to ensure accuracy. There are various types of transducers, from strain-gauge to piezoelectric, each suited for specific ranges of pressure and types of measurements.
Applications in Fluid Dynamics
Aerodynamics and Hydrodynamics
The dynamic pressure is an important factor in both aerodynamics and hydrodynamics. Particularly, it is utilized in determining the pressure coefficient of an object in motion through a fluid.
The pressure coefficient is a dimensionless parameter defined as the ratio of the static pressure to the dynamic pressure. This value is used to describe the pressure distribution around a body moving through a fluid, such as air or water, providing a normalized measure of the pressure at a specific point on the object’s surface relative to the free-stream pressure.

In aerodynamics, the pressure coefficient is frequently employed to analyze the lift and drag characteristics of airfoils and wings. For instance, it is used to visualize how pressure changes along the upper and lower surfaces of an airfoil, which is essential for understanding lift generation.
Similarly, in hydrodynamics, the pressure coefficient is used to study the pressure distribution around objects submerged in water. This is particularly important in fields such as ship design and offshore engineering.
Boundary Layer Flow
The dynamic pressure also has a significant impact on the development and behavior of the boundary layer, particularly the skin friction coefficient. This coefficient is a dimensionless parameter used in fluid dynamics to measure the effects of viscous forces on a surface, defined as the ratio of skin friction to dynamic pressure. Understanding the skin friction coefficient is important in assessing the drag experienced by a surface in boundary layer flow, as it relates frictional forces to the kinetic energy of the flow.
