Strain measures the deformation of an object when an external force is applied. Normal strain occurs when the force acts perpendicularly to the surface, causing elongation or contraction, while shear strain results from parallel forces producing angular distortion. The stress-strain relationship enables understanding of material behavior and is used by engineers for structural design and materials selection.
Overview of Strain
Strain is a measure of the deformation experienced by an object when subjected to an external force. It is a dimensionless quantity and can manifest in two major forms: normal strain and shear strain. Normal strain occurs when the deformation is parallel or perpendicular to the direction of the applied force, while shear strain measures the deformation as a result of forces applied parallel to the surface of the object, causing a change in shape.
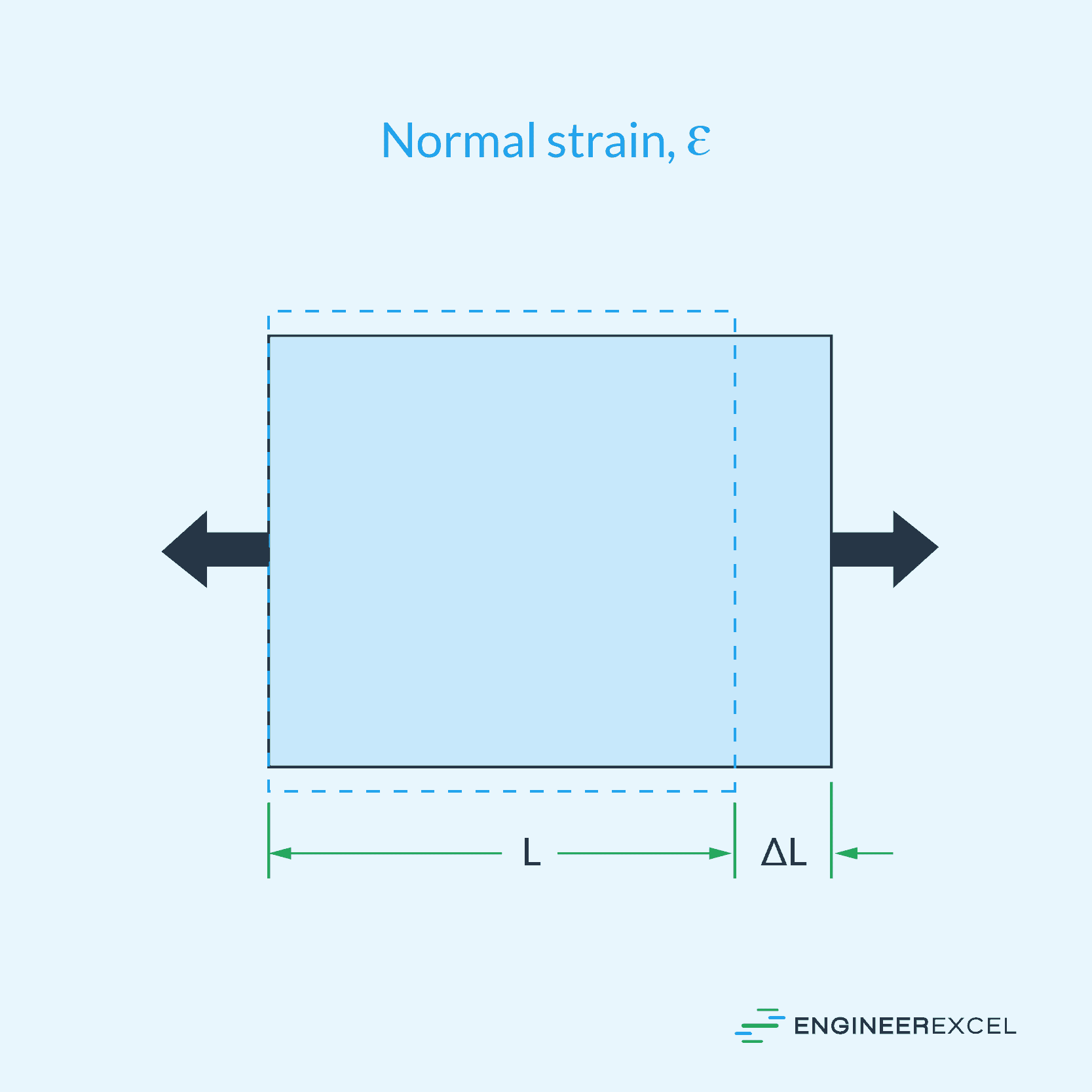
The normal strain is defined by the ratio of the change in length (ΔL) to the original length (L) of the material and is denoted by the Greek letter epsilon (ε). Positive values of normal strain correspond to tensile strain, while negative values represent compressive strain. Mathematically, normal strain can be expressed as:
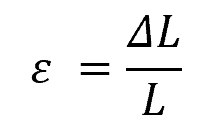

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
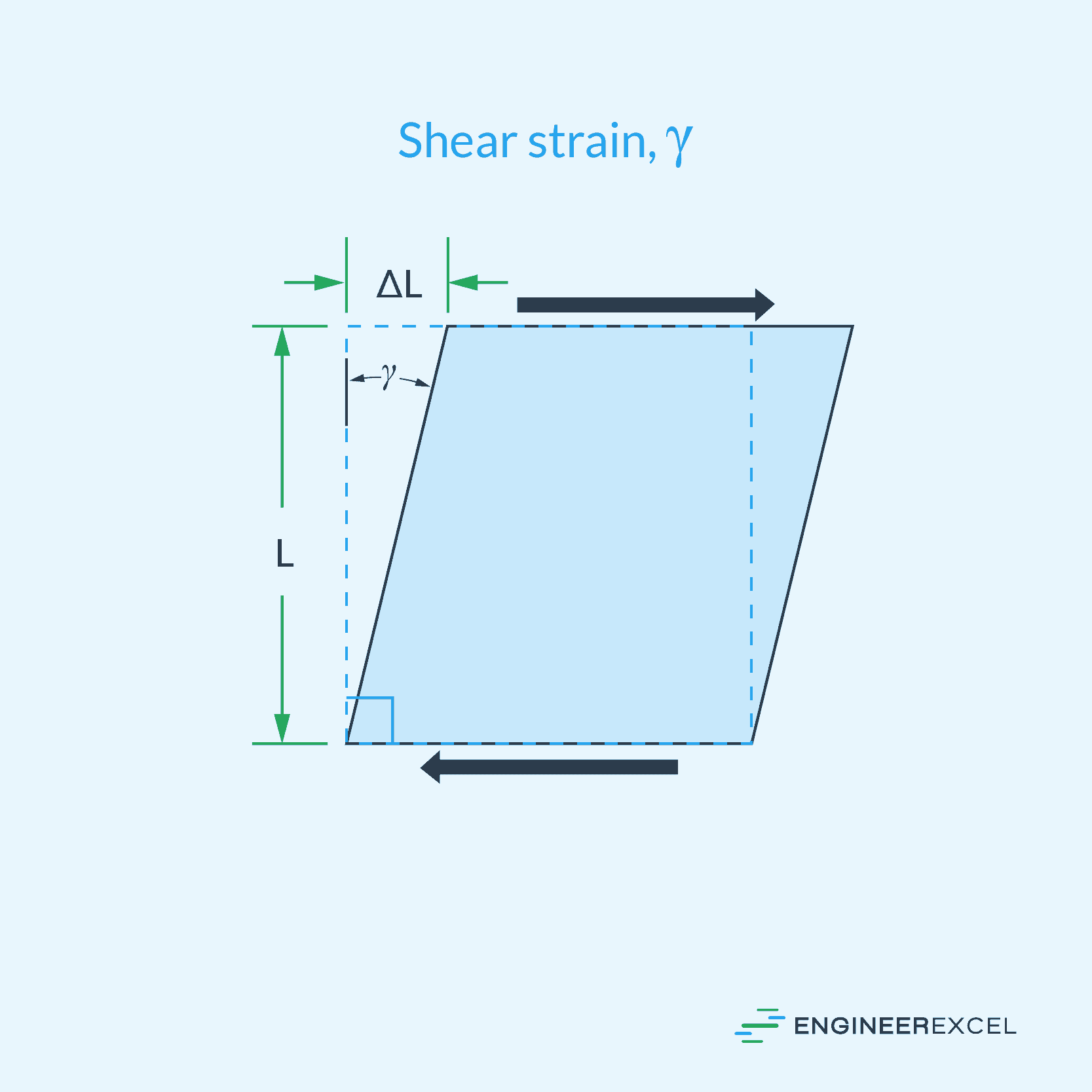
On the other hand, shear strain quantifies the rotational deformation caused by forces acting tangentially to the surface of the object. It is represented by the Greek letter gamma (γ) and is calculated by dividing the deflection of a face (ΔL) by the length of the face (L). The formula for shear strain is:
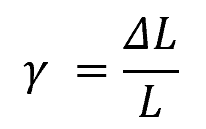
The mechanical properties of materials play a crucial role in determining their response to stress and strain. One such property is Young’s Modulus (E), which defines the relationship between normal stress and normal strain. It is given by the ratio of stress (σ) to strain (ε):
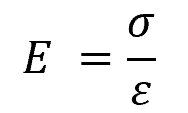
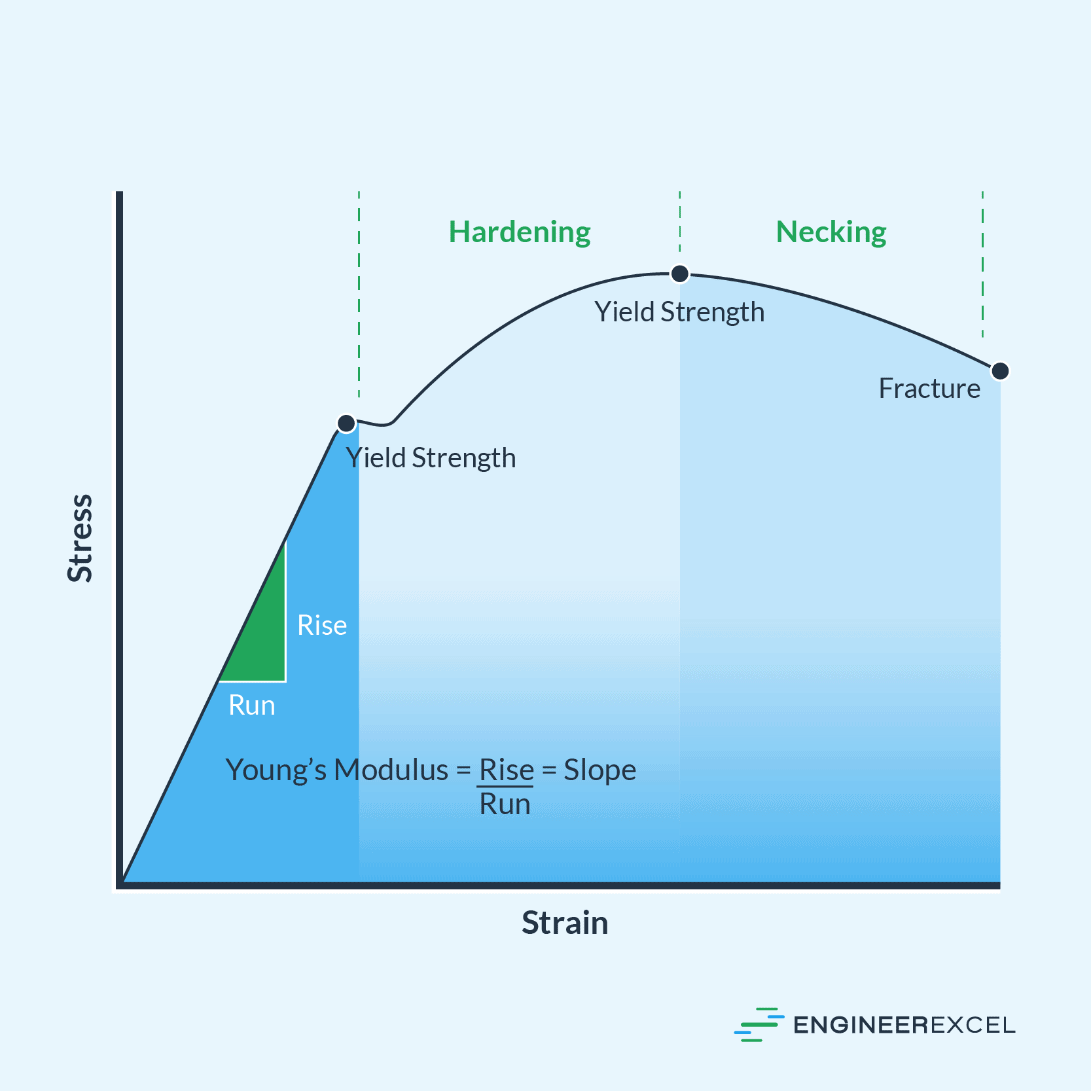
This relationship is often represented graphically in the form of stress-strain curves, which show the various regions of material behavior, such as the elastic, hardening, and necking regions. These curves help engineers and material scientists understand how different materials respond to applied forces and select suitable materials for specific applications.
Fundamental Concepts of Normal Strain
Normal strain is a measure of the deformation experienced by a material when subjected to an external force. This type of strain occurs when the force is applied perpendicular to the material’s surface, in contrast to shear strain, which arises from parallel forces. Understanding normal strain is crucial for evaluating a material’s behavior under load and ensuring its structural integrity.
Materials subjected to normal strain undergo a change in their dimensions. For example, when a rod is stretched or compressed along its length, its cross-sectional dimensions may change as well. The extent to which a material deforms under normal stress depends on its mechanical properties, such as elasticity and strength.

Normal strain, which is a unitless ratio, represents the proportional change in a material’s dimensions due to the applied force. Consequently, a positive normal strain suggests elongation, while a negative one indicates compression.
The analysis of normal strain often involves the use of stress-strain graphs. This graphical representation helps to visualize the relationship between stress and strain in a material, enabling a better understanding of its mechanical behavior.
Another critical aspect of normal strain analysis is the generalized Hooke’s law, which relates stress and strain considering any loading and temperature change. This law is based on the assumptions of homogeneous and isotropic material properties, linear elastic deformation, and small strains. Hooke’s law plays a pivotal role in determining the elastic modulus, a material property that quantifies its ability to withstand deformation under stress.
Determination of Normal Strain
An accurate way to determine normal strain is by first obtaining the stress-strain curve of the material. A stress-strain curve exhibits the relationship between an applied stress and the resulting strain it causes. Materials tests provide valuable data for constructing these curves.
Once the stress-strain curve is obtained, the normal strain can be determined through the curve’s slope. This slope represents the material’s elastic modulus or Young’s modulus (E). With the Young’s modulus known, one can determine the normal strain when a specific stress is applied. This is done by rearranging the equation above and isolating the strain (ε):

It is crucial to consider the material’s linear elastic region only, where Hooke’s Law is valid, and the stress is directly proportional to the strain. In this range, the material returns to its original shape once the force is removed.
Units and Measurement of Normal Strain
Imperial Units
In the Imperial unit system, strain is expressed in inches per inch (in/in) or microinches per inch (μin/in) for very small strains. Since strain is a dimensionless quantity, these units merely indicate the relative change in length. For example, a strain of 0.001 in/in represents an elongation of 0.001 inches for each inch of the original length.
SI Units
The International System of Units (SI) is the most widely used system for strain measurement. In this system, strain is expressed as a dimensionless quantity without any specific units, though it is often written using the metric length unit, meters (m). The most common strain measurement in SI units is microstrain (µε), which is equal to 1 x 10⁶ of the original length.
For example, a strain of 1 µε represents a deformation of one-millionth (10⁻⁶) of the original length. If the original length was one meter, the elongated length would be 1.000001 meters.
Types of Normal Strain
Normal strain occurs when a force is applied perpendicular to an object’s surface. There are two primary types of normal strain: tensile strain and compressive strain. These strains can significantly impact various materials and their properties.
Tensile Strain
Tensile strain occurs when a material is subjected to a stretching force, causing it to elongate. As the material lengthens, its cross-sectional area may also decrease. Tensile strain can lead to the formation of microscopic cracks, which may grow over time, potentially causing structural failure. Materials such as metals, plastics, and composite materials are often subjected to tensile testing to determine their mechanical properties under tensile loading.
Compressive Strain
Compressive strain arises when a material is subjected to a compressive force, causing it to shorten. This compression usually results in an increase in the material’s cross-sectional area, leading to a decrease in its length.
Compressive strain influences the material’s mechanical properties, such as its stiffness and stability under compression. It can also lead to material buckling, which can cause catastrophic failure in structures like columns and struts. To understand how materials behave under compressive loading, engineers often perform compression tests and analyze the stress-strain diagrams for materials like concrete, foams, and ceramics.
Effects of Normal Strain
Deformation
Normal strain is a measure of the deformation or change in dimensions an object undergoes when subjected to an external force. When a material experiences normal stress (perpendicular to a surface), it either elongates or contracts in the direction of the applied force. A positive normal strain value indicates tensile (an elongation) strain, while a negative value indicates compressive (a contraction) strain. Materials exhibit different behaviors like elastic deformation, plastic deformation, and fracture in response to normal strain and according to their mechanical properties.
Stress Generation
The relationship between normal stress and normal strain can be described by Young’s Modulus (E), which expresses the stiffness of a material. The stress generation within a material directly affects its mechanical performance. In the elastic region, a material returns to its initial shape and dimensions once the externally applied force is removed. However, when the stress exceeds the yield strength of the material, it enters the plastic region, causing permanent deformation.
Material Failure
Material failure occurs when the applied stress exceeds the material’s strength, causing fracture. The ultimate tensile strength (UTS) represents the maximum stress that a material can withstand before failure occurs. A material’s ductility or brittleness is determined by its ability to absorb energy or deform before fracture. Understanding normal strain and its effects on deformation, stress generation, and material failure helps engineers to select appropriate materials and design structures capable of withstanding various loading conditions.
Example Problem: Normal Strain
Consider a straight cylindrical rod made of a homogeneous and isotropic material with a cross-sectional area A and an initial length L. If a tensile force F is applied at both ends of the rod, the rod will experience elongation (ΔL). The objective of this example is to determine the normal strain (ε) experienced by the rod due to this elongation.
Given values:
- Initial length (L) = 2m
- Cross-sectional area (A) = 0.01 m²
- Applied force (F) = 1000 N
The normal stress (σ) can be calculated using the following formula:

Plugging the given values into the formula:
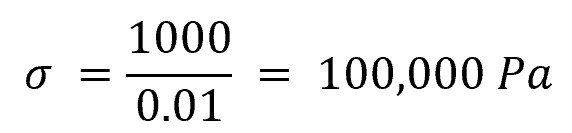
Now, we need to use the material’s elastic properties, specifically the Young’s modulus (E) to relate stress and strain. Suppose the given Young’s modulus for this material is:
- Young’s modulus (E) = 200 GPa = 200 x 10⁹ Pa
The relationship between stress, strain, and Young’s modulus can be described by the formula:

By substituting the calculated stress and the given Young’s modulus into the formula, we can calculate the normal strain:
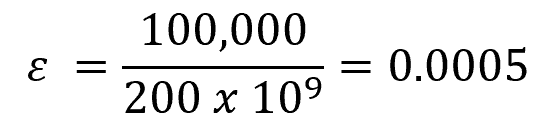
Hence, the normal strain experienced by the rod is 0.0005.
Applications of Normal Strain
Engineering Structures
In civil and mechanical engineering, the analysis and design of structures rely heavily on understanding how materials respond to stress and strain. Normal strain is especially important when considering the structural integrity and stability of bridges, buildings, and other large-scale infrastructure elements. By evaluating the normal strain induced in these structures, engineers can determine whether or not a design is capable of withstanding anticipated loads, or if modifications are needed to improve the structural performance. Additionally, engineers can utilize the strain data to identify potential stress concentrations or areas prone to failure in existing structures.
Materials Testing
Measuring normal strain is a fundamental practice in materials testing, where the objective is to characterize the mechanical properties of various materials. In typical tensile and compression tests, samples are subjected to forces perpendicular to their surface. Engineers analyze the normal strain experienced by the material, along with the corresponding stress, to determine key mechanical properties such as the elastic modulus, yield strength, and ultimate tensile strength. These properties are essential in selecting appropriate materials for various applications, and understanding their behavior under real-life service conditions.

Biomechanics
Lastly, the study of normal strain in biomechanics is essential to understanding the behavior and mechanics of biological tissues and their responses to various forces. By examining the strain experienced by soft and hard tissues, like tendons and bones, during loading and unloading, researchers can gain insight into the mechanical properties of these biological materials and their responses to stress. Studying normal strain in biomechanics can help improve the design of prosthetics, orthotic devices, and sports equipment, as well as inform rehabilitation techniques and injury prevention strategies.
