Normal stress, also known as tensile or compressive stress, is a measure of the intensity of internal forces acting on a material perpendicular to a given cross-sectional area. Tensile stress occurs when forces act to elongate a material, while compressive stress results from forces that squeeze a material. In this article, we will discuss the concept of normal stress, its calculation, and the relationship between normal stress and normal strain
What is Normal Stress
Normal stress, denoted by the symbol σ, refers to the internal force applied perpendicular to the cross-sectional area of a material. Depending on the material deformation caused by the force, there are two primary types of normal stress: tensile stress and compressive stress.

Tensile stress occurs when forces act to stretch or elongate an object. The applied force tries to pull the material apart, creating tension within the material. In this situation, the normal stress is positive, as it acts away from the surface.
Tensile stress can cause deformation and eventual failure in materials that are unable to withstand the stretching forces. For example, bridges and cables experience tensile stresses when subjected to loads that stretch them across long spans.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
Compressive stress occurs when forces act to compress or shorten an object. The applied force pushes the material together, creating pressure within the material. In this situation, the normal stress is negative, as it acts towards the surface.
Compressive stress can result in crushing, buckling, or fracturing of a material, particularly in structural engineering applications such as building columns, subjected to heavy loads from above.
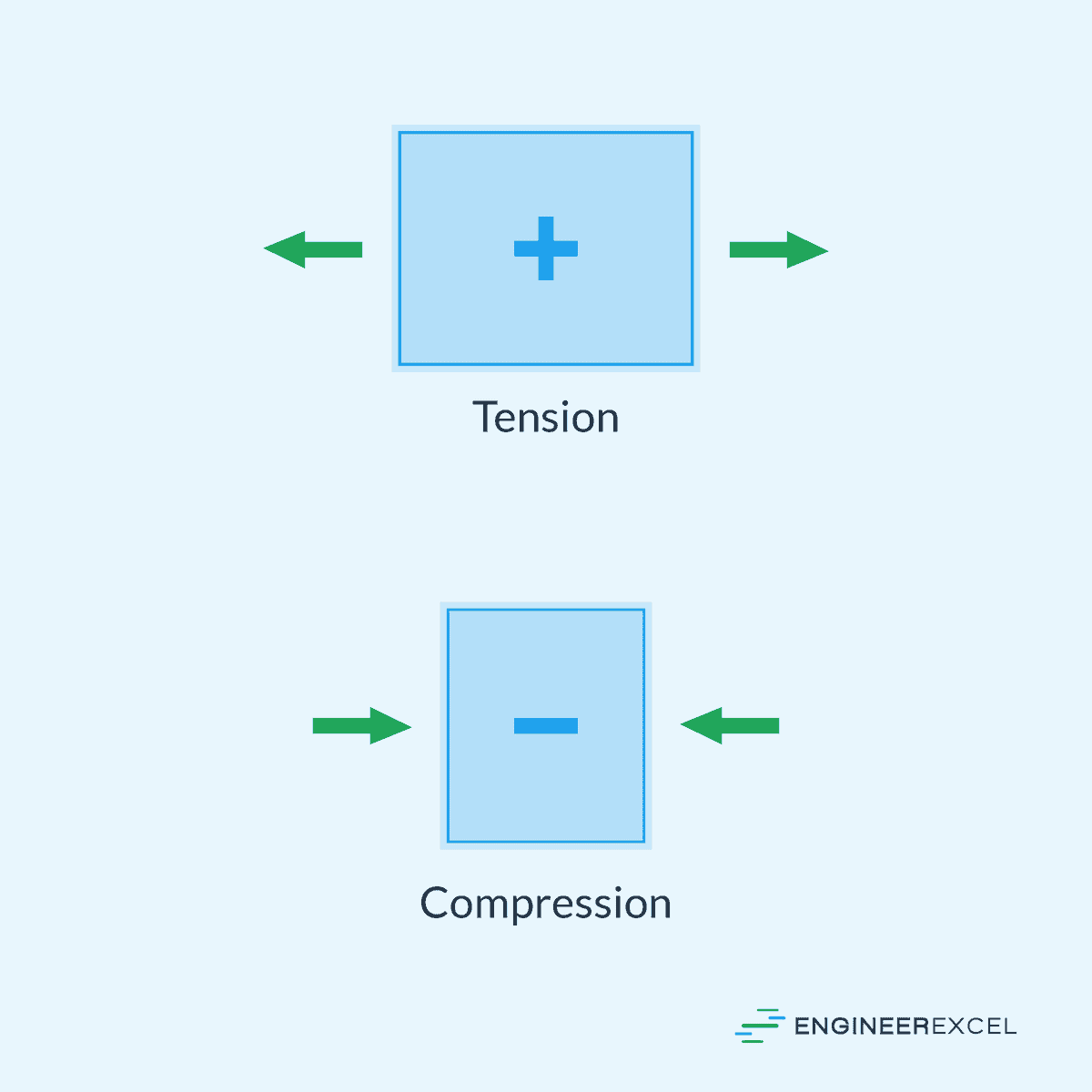
The distinction between tensile and compressive stress is important in the selection of materials and the design of structures. Engineers must consider both types of stress when evaluating the performance and failure modes of a material.
For instance, concrete is robust under compressive stress but weak under tensile stress, making it crucial to reinforce it with steel bars in applications where both stresses are present. In contrast, materials like steel are more versatile, as they can handle both tensile and compressive stress effectively.
Normal Stress Calculation
The formula for calculating normal stress depends on the type of loading.
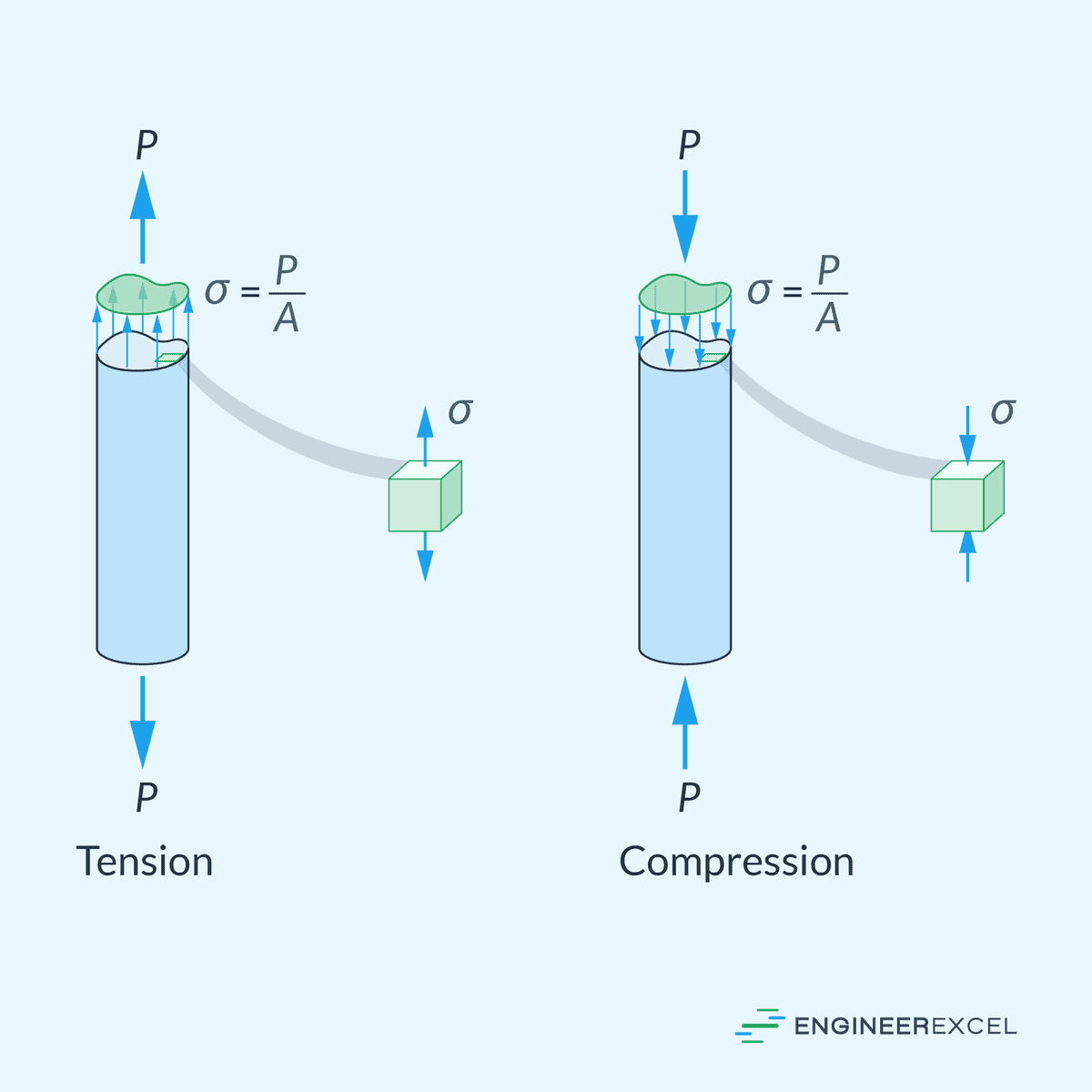
For a material subjected to a uniaxial load, such as the diagram shown above, normal stress can be calculated using the following formula:

Where:
- σ = average normal stress due to axial load [Pa]
- P = applied axial load [N]
- A = cross-sectional area of the structure [m2]
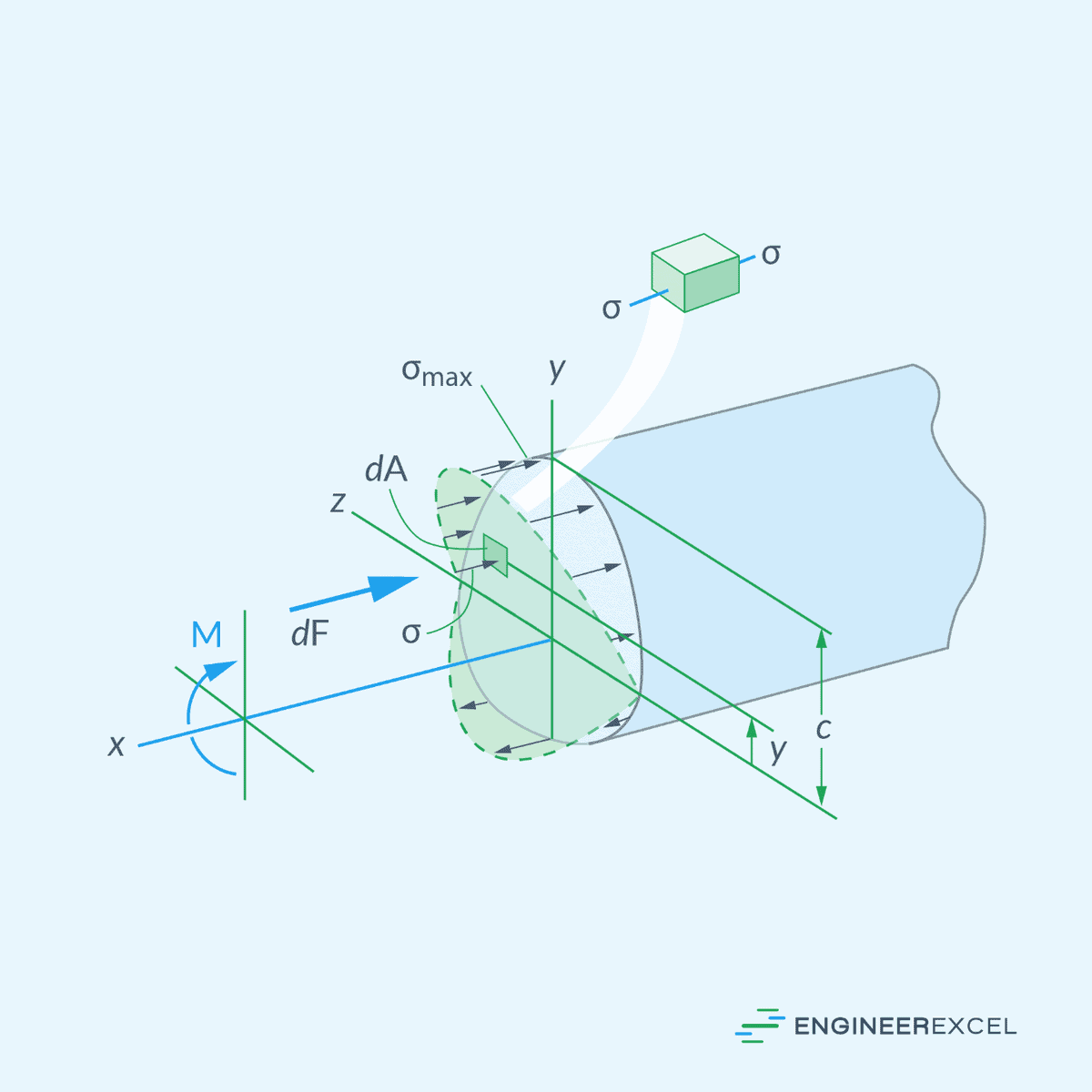
On the other hand, for a material subjected to a bending moment, the normal stress distribution can be described using the following equation:
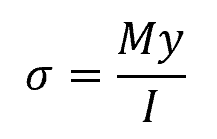
Where:
- σ = normal stress due to bending [Pa]
- M = applied bending moment [N-m]
- y = distance from the neutral axis to the point at which the stress is being calculated [m]
- I = moment of inertia [m4]
Notice that, when a structure experiences an axial load, the normal stress distribution is uniform across the cross-section. In contrast, when subjected to a bending moment, the normal stress distribution varies linearly, reaching maximum tensile and compressive stresses at the outermost fibers and zero stress along the neutral axis. The neutral axis is the line within the cross-sectional plane where the material experiences neither tension nor compression.
Normal Stress vs Normal Strain
Another parameter that is closely related to normal stress is the normal strain. Denoted by the symbol ε, it is a dimensionless quantity that provides a quantitative measure of how much a material deforms under the influence of normal stress.
Normal strain is defined as the ratio of the change in length to the original length of the material, expressed mathematically as:
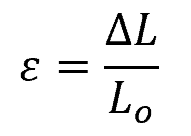
Where:
- ε = normal strain [unitless]
- ΔL = change in length of the structure [m]
- Lo = original length of the structure [m]
The relationship between normal stress and normal strain is governed by Hooke’s Law for linear elastic materials. Mathematically, this relationship is represented as:
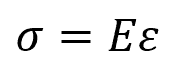
Where:
- E = modulus of elasticity [Pa]
This equation signifies that the normal stress is directly proportional to the normal strain, and the constant of proportionality is the modulus of elasticity. Essentially, Hooke’s Law describes how materials respond elastically to applied forces, allowing engineers to predict deformation based on the applied stress.
