Young’s modulus is an important physical property of any material. It describes how easily a material stretches or bends. When a force is applied to a material, that material will change shape. Every material will have an intrinsic amount that it can change before it begins to deform. This amount of change is the Young’s modulus of the material.
The Young’s modulus of a material is a constant value under given environmental parameters. When looking for a material with specific properties, it is important to understand the environment in which the material will be used, as different temperatures or pressures will impact the material properties, not just the Young’s modulus.
Understanding Young’s modulus
Young’s modulus, E, is calculated using the following formula:
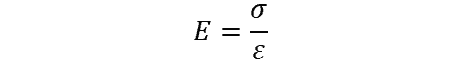

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
where:
- σ is the stress, measured in force per unit area (N/m^2 in SI)
- ε is the strain, i.e., the ratio of the change in length to the original length
Since strain is a dimensionless value, the units of Young’s modulus are the same as those of the stress. The image below shows the relationship between the stress and strain of a material as a force is applied.
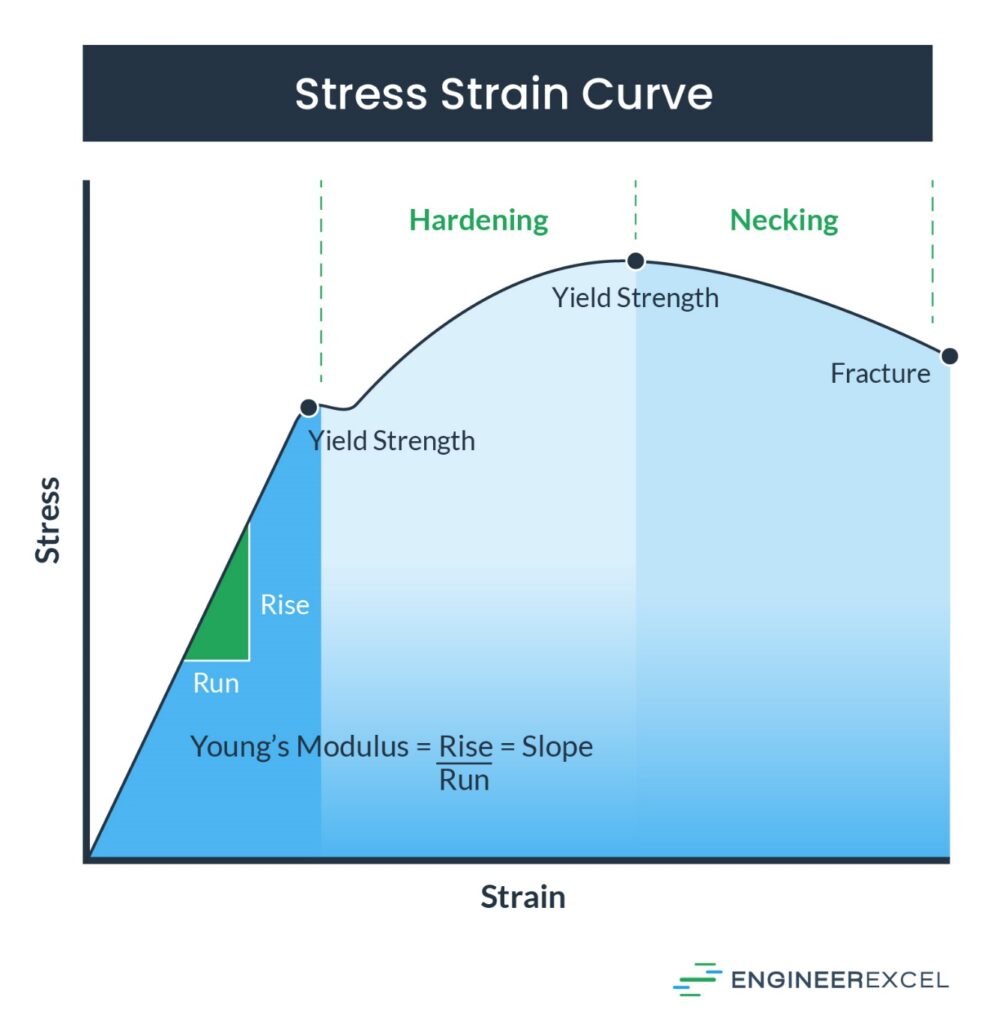
In the above image, as a force is applied, the material stretches or bends until it reaches its yield strength. If the force is removed before the yield strength is reached, the material will return to its original size and shape. However, if the force continues to be applied, the internal structure of the material will be permanently changed.
A good way to think about what is happening as a force is applied to a material is a rubber band, something that has a high Young’s modulus. The rubber band can be stretched and returns to its original shape when the stretching is stopped. However, if the rubber band is stretched too far, it will surpass its Young’s modulus, reaching its yield strength and passing quickly past its ultimate strength to failure.
Young’s modulus components
As stated, Young’s modulus is the ratio of how much stress to how much strain a material experiences before it begins to deform.
Stress
When a force is applied to a structure, that force will introduce a stress on the structural material. The stress is calculated using the following formula:
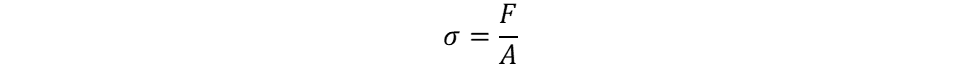
where:
- F is the force applied (N in SI)
- A is the cross-sectional area that the force is acting on (m2 in SI)
The figure below shows an example of a force acting parallel to the end of a beam.
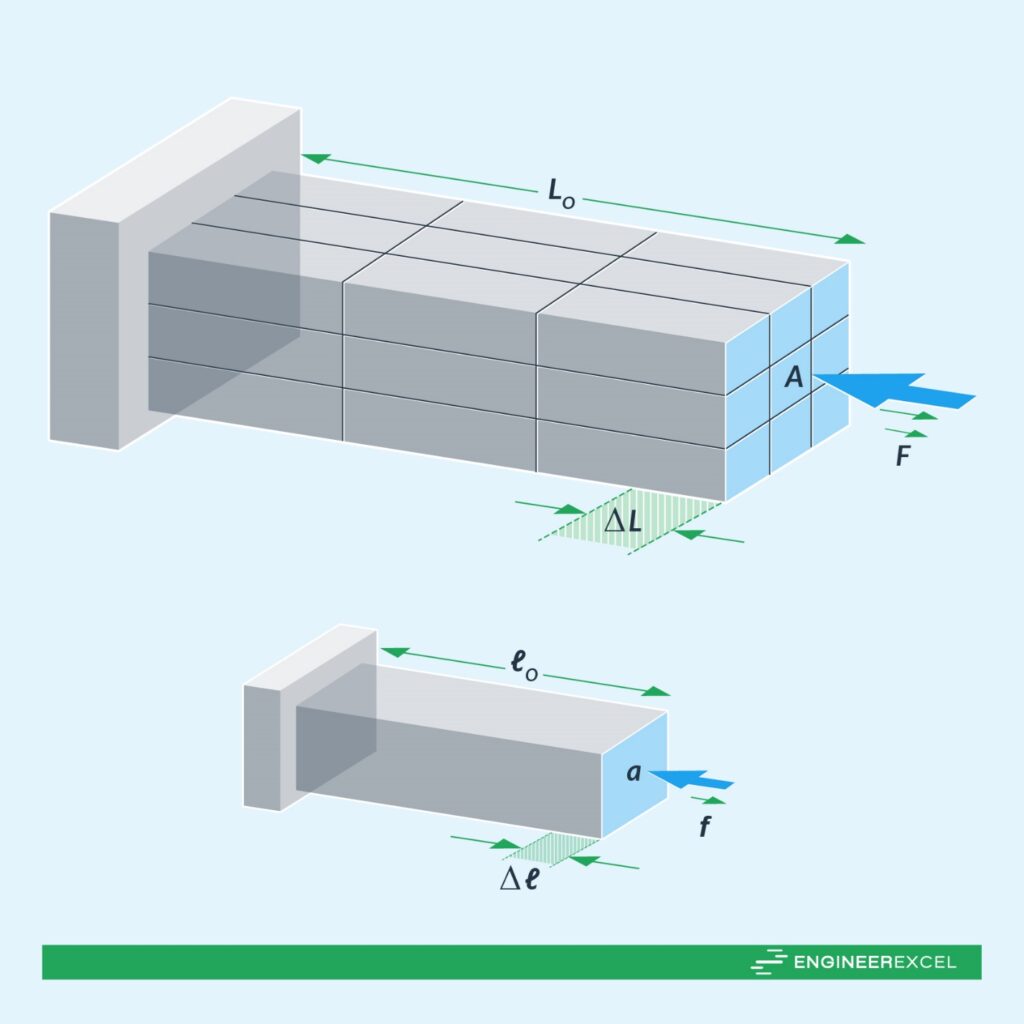
Strain
Additionally, when a force is applied to a structure, that structure will experience strain. This strain is a measure of how much the structure changes in relation to its original shape. The strain of a structure is calculated with the following formula:
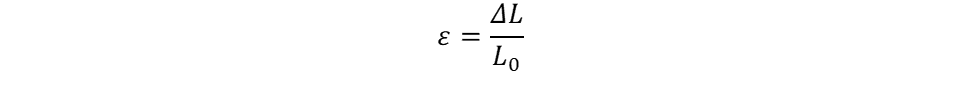
where:
- ΔL is the change in the length (m in SI)
- L0 is the original length (m in SI)
Applying Young’s modulus
Young’s modulus is used to determine appropriate materials for a design. As every material has a different Young’s modulus, it is necessary to understand what different values mean.
High Young’s modulus materials
A material with a high Young’s modulus is considered a stiff material. These materials, which include steel and titanium, can withstand large forces, and will exhibit very small changes in shape. To design a structure that will not change its shape or deform under large applied forces, such as in the design of a bridge or building, consider materials with a high Young’s modulus.
Low Young’s modulus materials
A material with a low Young’s modulus is considered an elastic material. These materials, which include rubber and foam, will experience a large change in shape as a force is applied. When designing something to store elastic energy, such as a spring, consider materials with a low Young’s modulus.
Materials with different Young’s modulus values are shown in the graph below:
Determining Young’s modulus
While the Young’s modulus of many materials has been determined, new alloys and materials developed can exhibit different properties, and so must be evaluated independently. The most common method for determining the Young’s modulus of a material is a tension test. In this test, a material sample is subjected to a tensile force as its elongation is measured. From the data gathered, a stress-strain curve can be created through material failure.

Because different materials will be used under different conditions, it may be beneficial for an engineer to determine the Young’s modulus using something other than a tensile test. Although the properties of a material are constant, using a compressive test on bulky materials that are likely to be subject to compression rather than tension may be advantageous. This test is the same as a tensile test, except the sample is compressed and its shortening is measured.

Extended applications of Young’s Modulus
While knowing and understanding a material’s Young’s modulus is important for an engineer, there are other properties that can be calculated from Young’s modulus that can also prove useful. An example of one such property is the specific stiffness of a material.
The specific stiffness is the Young’s modulus divided by the density of the material and may be referred to as the specific modulus. The specific stiffness is used when the weight of a material is important, such as in the design of an aircraft where a strong but lightweight material is needed. The specific stiffness of different materials can be easily compared to determine the material that will meet the strength and weigh requirements of a project.
