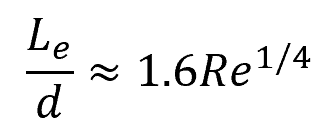Fluid mechanics defines a fully developed flow as having a constant velocity profile along the flow direction. This type of flow is characterized by the absence of a net force or component of force in the primary flow direction and the presence of constant shear stress at the boundaries.

This article explores the characteristics of fully developed flow, including its velocity profile and entrance length.
What is a Fully Developed Flow
A fully developed flow is a type of fluid flow in which the velocity profile remains unchanged along the flow direction. In such a flow, all the fluid properties, including velocity and temperature, remain constant along the primary flow direction.
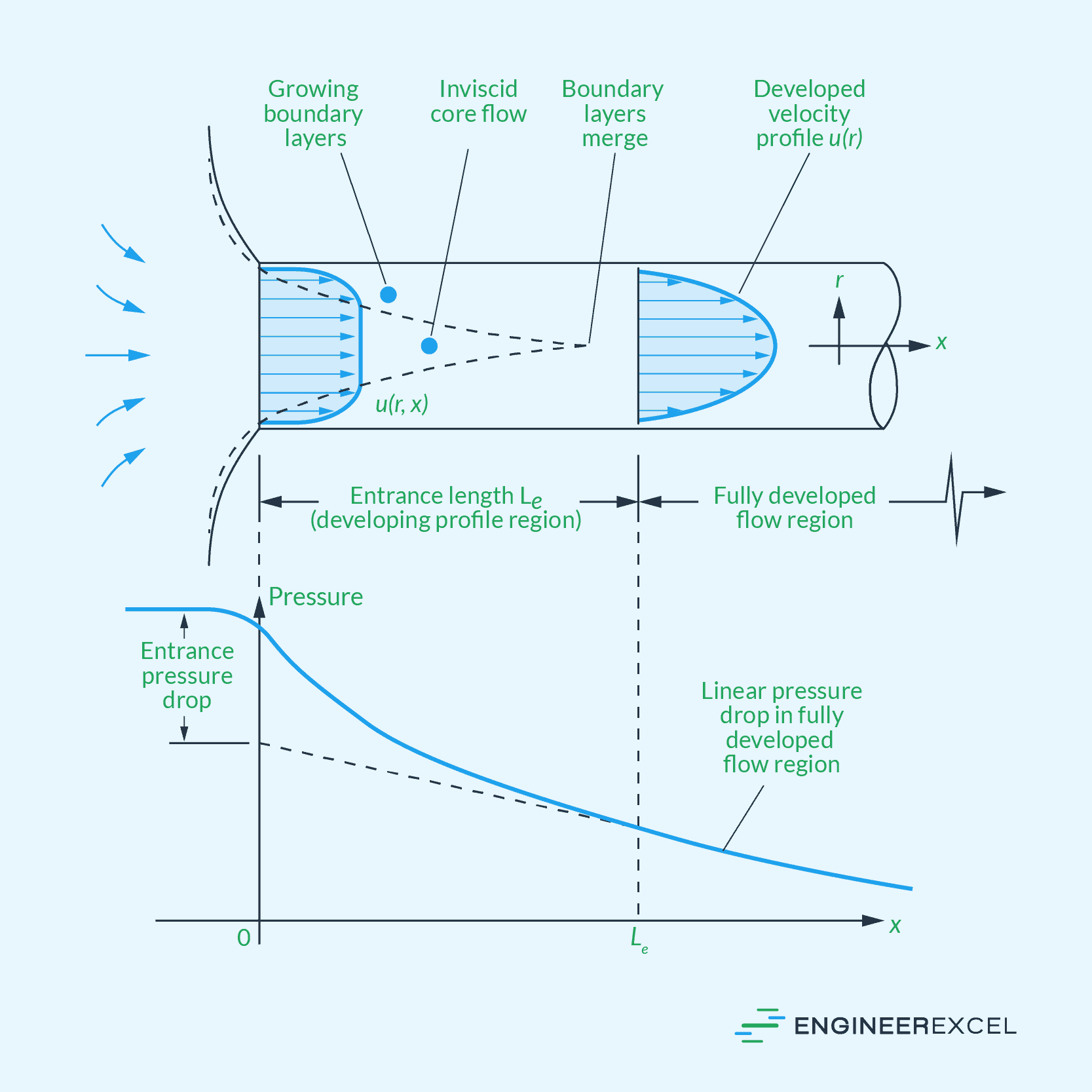
This steady state occurs after the fluid has passed through a developing region where the properties change substantially, as shown in the diagram below. In this region, the pressure drops linearly, for either laminar or turbulent flow. In engineering applications, fully developed flow is particularly relevant in pipes, channels, and ducts, as it helps simplify analyses and calculations of fluid behavior.
Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
One of the main characteristics of fully developed flow is the absence of a net force or a net component of force in the primary flow direction. This is because the inertial forces resulting from fluid acceleration are balanced by the viscous forces that oppose flow motion. Another characteristic is the presence of a constant shear stress at the boundaries, such as the walls of a pipe or channel.
Fully Developed Flow vs Developing Flow
Developing flow, on the other hand, refers to the region where the fluid properties change significantly along the flow direction. In this region, the velocity profile evolves from an initial non-uniform distribution to a constant one as the flow progresses. A developing flow typically occurs close to the entrance of a pipe or channel, where the fluid has just begun to flow and has not yet fully adjusted to the geometry of the conduit.
Fully developed flow differs from developing flow in several aspects. Firstly, in a fully developed flow, the velocity profile remains constant along the flow, meaning there is no further change in fluid properties along the flow direction, as opposed to a developing flow where these properties continue to evolve. Secondly, the shear stress at the boundaries in fully developed flow is constant, making it easier to analyze and calculate the pressure drop across the flow, as opposed to a developing flow where the shear stress is changing nonlinearly.
Velocity Profile in Fully Developed Flow
The general shape of the velocity profile in a fully developed flow depends on the flow regime— whether laminar or turbulent.
Fully Developed Velocity Profile in Laminar Flow
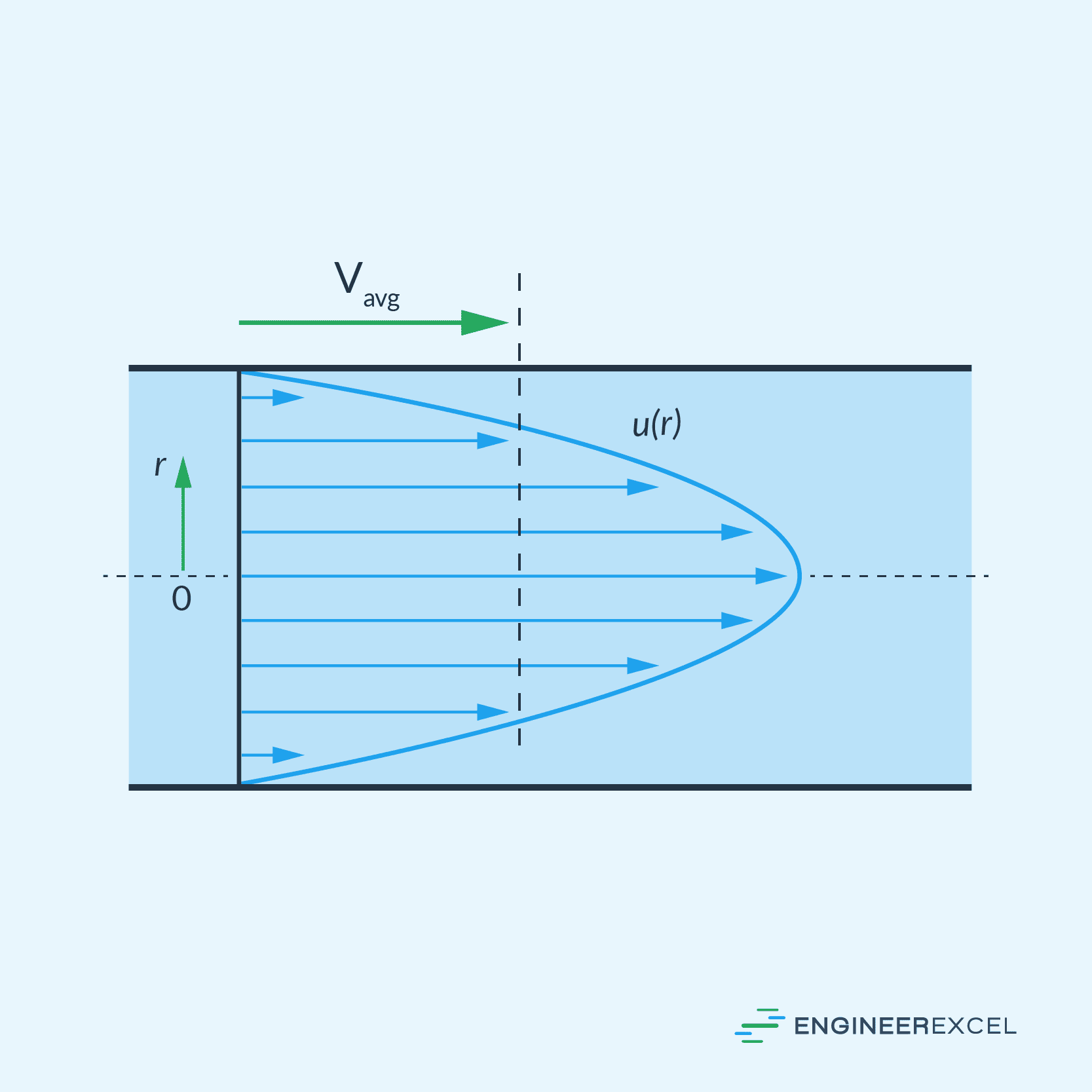
In laminar flow, fluid particles move in parallel layers with negligible mixing between layers. The velocity profile in a fully developed laminar flow within a pipe can be described using the Hagen–Poiseuille equation:

Where:
- u(r) = velocity of fluid at a distance r from the center of the pipe [m/s]
- ΔP = pressure drop across the length of the pipe [Pa]
- R = pipe radius [m]
- μ = fluid dynamic viscosity [Pa-s]
- L = length of the pipe [m]
The velocity profile is parabolic, with maximum velocity at the center of the pipe and zero velocity at the pipe wall, as shown in the figure below.
The average velocity can be calculated as:
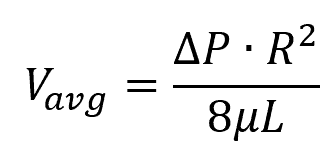
Where:
- Vavg = average fluid velocity [m/s]
Fully Developed Velocity Profile in Turbulent Flow
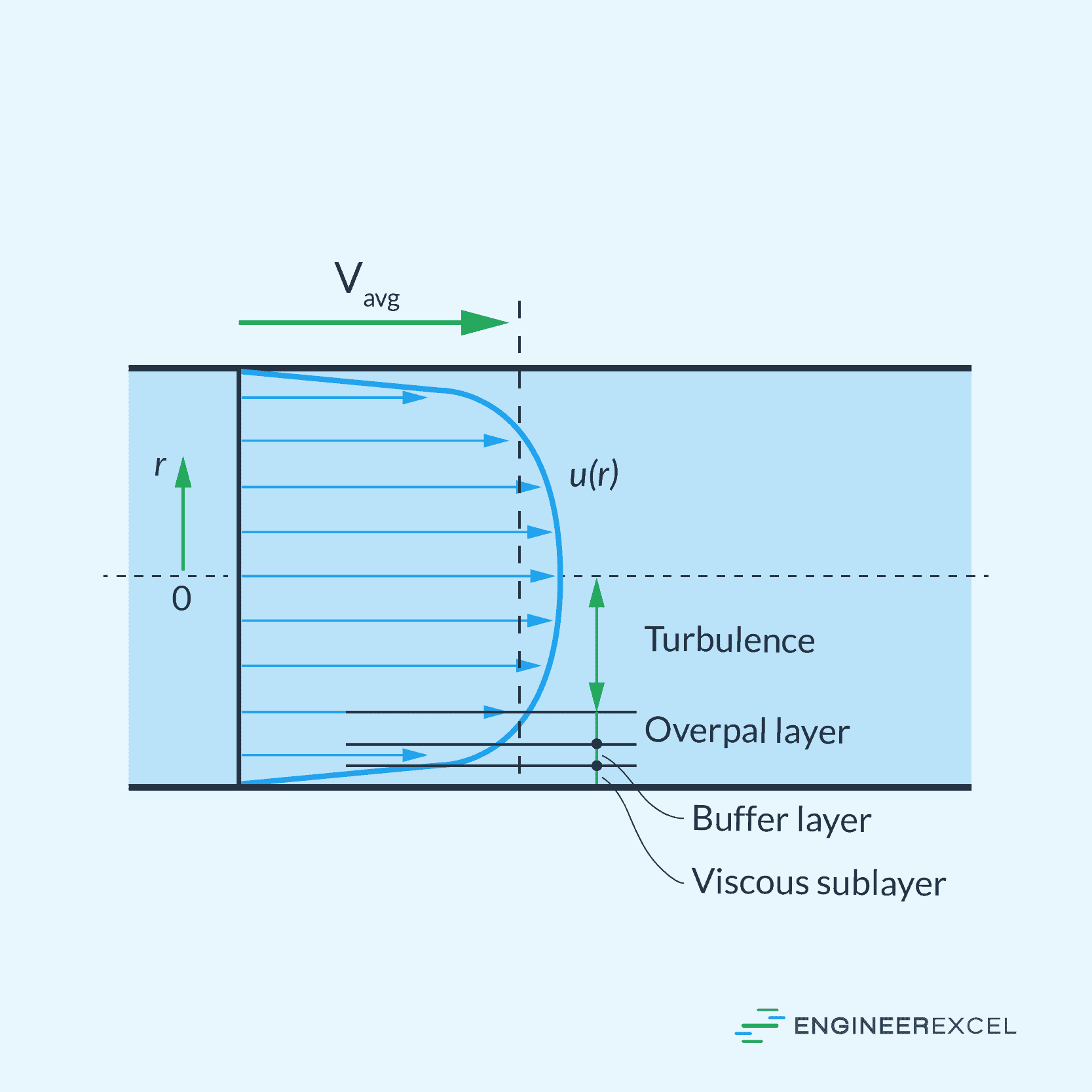
In turbulent flow, the fluid particles move in a chaotic motion, with rapid, irregular fluctuations of velocity and pressure. Hence, the velocity profile in a fully developed turbulent flow within a pipe is more complicated and is generally flatter compared to laminar flow, as shown in the figure below.
There are several empirical models that can be used to describe the velocity profile of a turbulent pipe flow. One of the simplest and widely used is the power-law velocity profile expressed as:
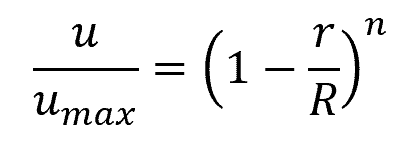
Where:
- umax = maximum fluid velocity at the center [m/s]
- n = power-law constant [unitless]
The value of n increases with increasing Reynolds number. The higher its value, the flatter the velocity profile. However, in many practical applications, it is assumed to be equal to 7.
Entrance Length for Fully Developed Flow
The entrance length is a critical parameter in understanding fully developed flow in a pipe or channel. It is the distance from the inlet of the pipe or channel to the point where the velocity profile becomes fully developed.
The entrance length depends on the Reynolds number, which is a dimensionless value representing the ratio of inertial forces to viscous forces in fluid flow. For laminar flow, the entrance length can be approximated using the following correlation:
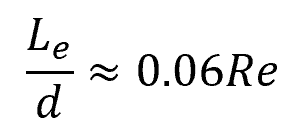
Where:
- Le = entrance length [m]
- Re = Reynolds number [unitless]
- d = pipe diameter [m]
For turbulent flow, the sixth-power-law estimate is the most widely used formula:
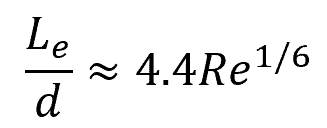
Alternatively, a more accurate correlation developed by F. Anselmet and S. Dash can be used: