Unsteady pipe flow occurs when the flow rate or velocity within a pipe varies with time. In this article, we’ll explore the causes, consequences, control strategies, and governing equations used to analyze unsteady pipe flow.
Unsteady Pipe Flow Explained
Unsteady pipe flow refers to the flow of fluid (usually a liquid or gas) through a pipe or conduit where the velocity, pressure, and other flow parameters change with respect to time. In other words, it is a flow situation in which the fluid’s characteristics vary over time, as opposed to steady-state flow where these characteristics remain constant.
What Causes Unsteady Pipe Flow
Unsteady pipe flow can be due to various factors. In general, it occurs when there is a sudden change in flow conditions, such as the opening or closing of a valve, a pump starting or stopping, or a sudden change in the inlet or outlet conditions.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
External forces or disturbances, such as vibrations or pressure fluctuations, can also cause unsteady flow behavior in a pipe. During these transitions, the flow parameters, such as the velocity, pressure, and density, change until they reach a new steady-state or quasi-steady-state condition.
However, in some applications, the flow in a pipe can be inherently pulsating. This means that flow varies periodically over time. For example, blood flow in arteries pulsates due to the beating of the heart.
Why Unsteady Flows Are Undesirable in Pipe Systems
Unsteady flows in pipe system can lead to several problems. They cause fluctuations in pressure and velocity, leading to potential failures and inefficiencies in the system. Additionally, unsteady flows may increase wear and tear on pipes, causing premature aging and increasing maintenance requirements.

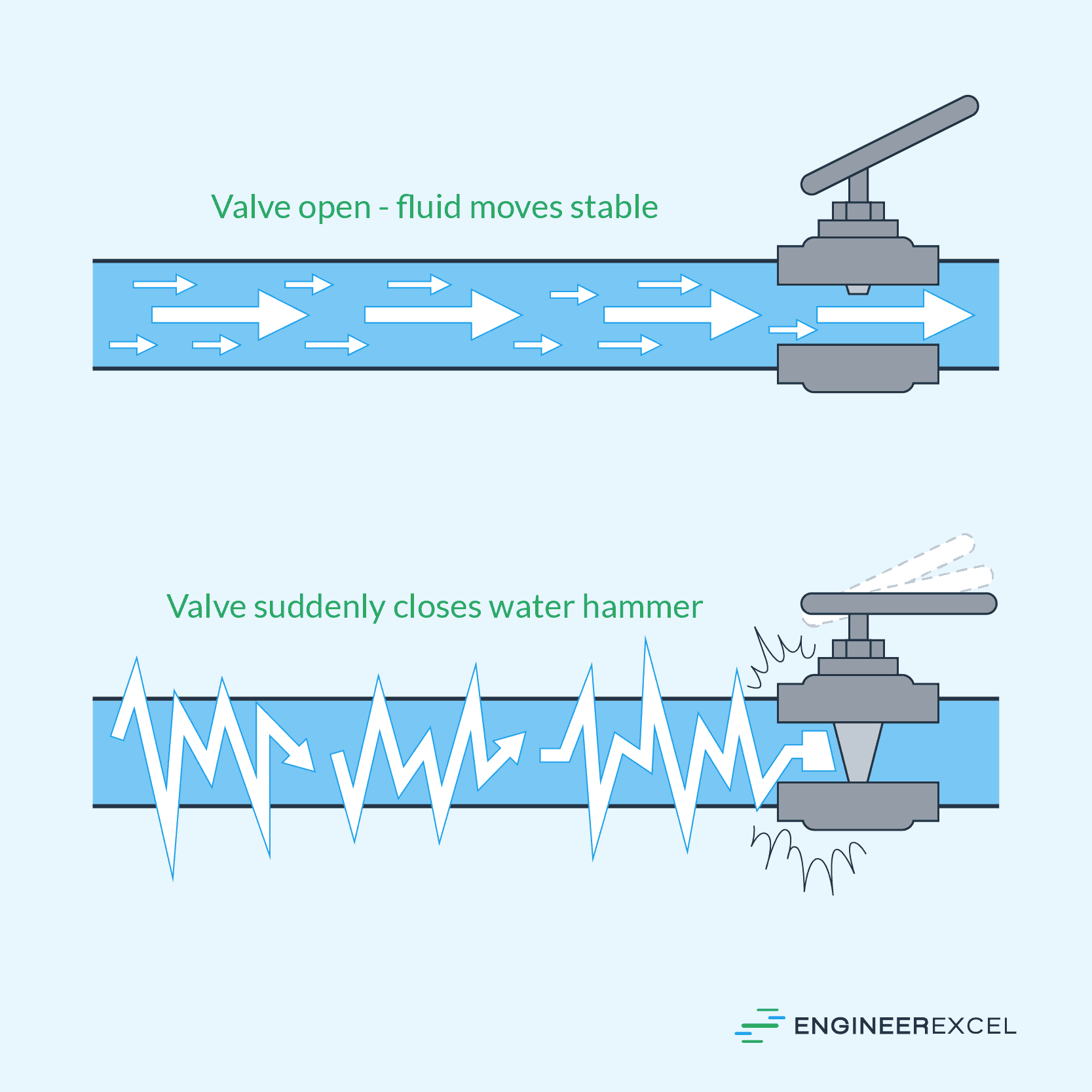
In some cases, unsteady flows can also lead to undesirable operational issues such as water hammer, which is the sudden change in pressure that occurs when the flow velocity changes rapidly. This phenomenon can result in shockwaves that cause damage to your pipe system and the equipment connected to it. The magnitude of a water hammer is dependent on a number of factors, including the rate of acceleration or deceleration of the fluid, the compressibility of the fluid, the elasticity of the pipe, and the overall geometry of the pipe system.
In general, striving to maintain steady flows in pipe systems helps to preserve the system’s life span, performance, and long-term maintenance costs.
Unsteady Pipe Flow Calculations
Calculating unsteady pipe flows is a complex process that involves solving unsteady state Navier-Stokes equations, which describe the conservation of mass and momentum for fluid flow. The nature of the flow, such as whether it is compressible or incompressible, laminar or turbulent, and whether it is single-phase or multiphase, affects the complexity of these equations. In general, numerical methods are used to perform these calculations.
The continuity equation and the equation of motion are the controlling equations for unsteady flow in a closed conduit. As there is no closed-form solution due to the quasilinear nature of these equations, methods such as the method of characteristics and centered-implicit solutions are used to deal with them. Boundary conditions must be set at the inlet and outlet, as well as any solid boundaries, and initial conditions for the flow variables are required.

To discretize the governing equations, numerical methods such as finite difference, finite element, or finite volume are used. The domain is broken down into a grid or mesh, and values are calculated at discrete points. Since this is an unsteady problem, the equations must be integrated over time using explicit or implicit schemes.
Numerical solvers or software packages designed for fluid dynamics simulations are used to solve the discretized equations. The process involves iterating through time steps until a steady-state or desired time period is reached. Once the simulation is complete, relevant flow parameters like velocity, pressure, and temperature can be extracted and visualized using contour plots, vector plots, or streamline plots.
Sensitivity analyses can be performed to investigate how changes in parameters or boundary conditions affect the results. Finally, the simulation results can be used to make informed decisions and adjustments for system optimization or design.
