Pressure and flow rate are fundamental properties in fluid dynamics that directly impact the performance and safety of fluid systems. Hence, it is crucial to understand their relationship, particularly when designing systems that involve fluid flow, such as hydraulic, pneumatic, aerospace, biomedical, and HVAC systems.

This article aims to provide a comprehensive overview of the equation that relates pressure and flow rate, including its applications, calculations, and the factors that affect it.
Understanding the Different Pressure Flow Rate Equations
There is no equation that can singlehandedly encompass the relationship between the pressure and flow rate of a fluid in motion. Different applications and conditions may involve different types of equations.
However, pressure and flow rate are closely related properties that may affect each other in one way or another. Pressure refers to the force per unit area that a fluid exerts on its surroundings, while the flow rate is the amount of fluid that passes through a given point in a unit of time. Note that the flow rate may either be in terms of the volume or mass of the fluid.
Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
This article discusses two different equations that relate to pressure and flow rate: Bernoulli’s Equation and Poiseuille’s Law.
Bernoulli’s Equation
Bernoulli’s equation relates the pressure, velocity, and height of a fluid undergoing steady flow. The general assumption of this equation is that the fluid is ideal and incompressible. “Ideal” means that the fluid has negligible internal friction and viscosity, while “incompressible” means that the amount of force needed to compress the fluid is extremely large, resulting in a uniform density all throughout.
These assumptions are crucial because of the complexity of fluid movement— that is, even basic fluid motion can lead to a complicated set of equations. By focusing on ideal fluids, calculations can be simplified, providing a useful baseline for investigation.
Derived from the principle of conservation of energy, the Bernoulli equation states that the total energy of a fluid is constant along a streamline. This includes the kinetic energy due to the fluid’s motion, the potential energy due to its height, and the pressure energy due to its pressure.
Bernoulli’s Equation Calculation
In its simplest form, Bernoulli’s equation can be mathematically written as:
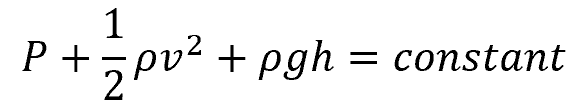
Where:
- P = pressure of the fluid [Pa]
- ρ = density of the fluid [kg/m3]
- v = velocity of the fluid [m/s]
- h = height of the fluid above a reference point [m]
- g = acceleration due to gravity [9.81 m/s2]
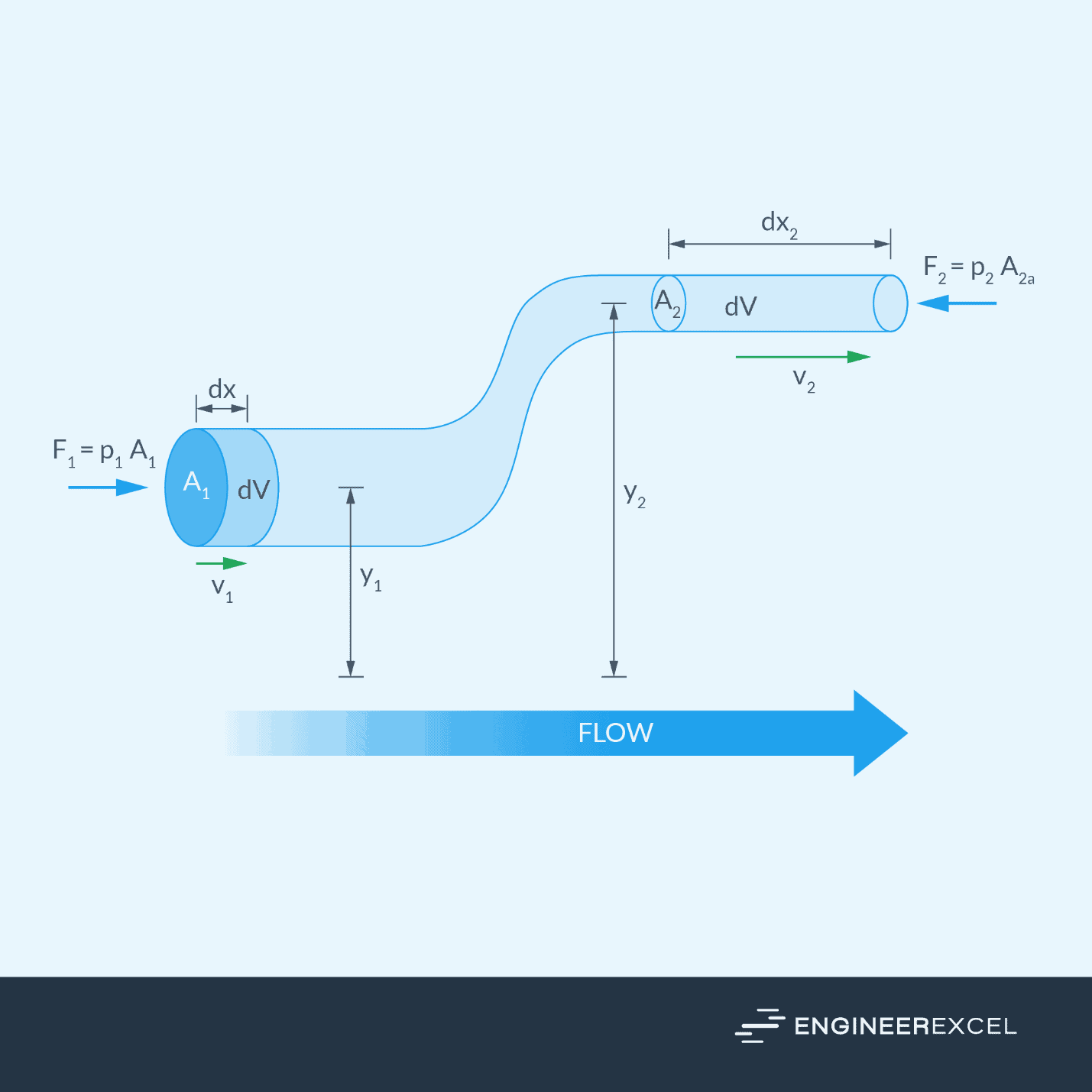
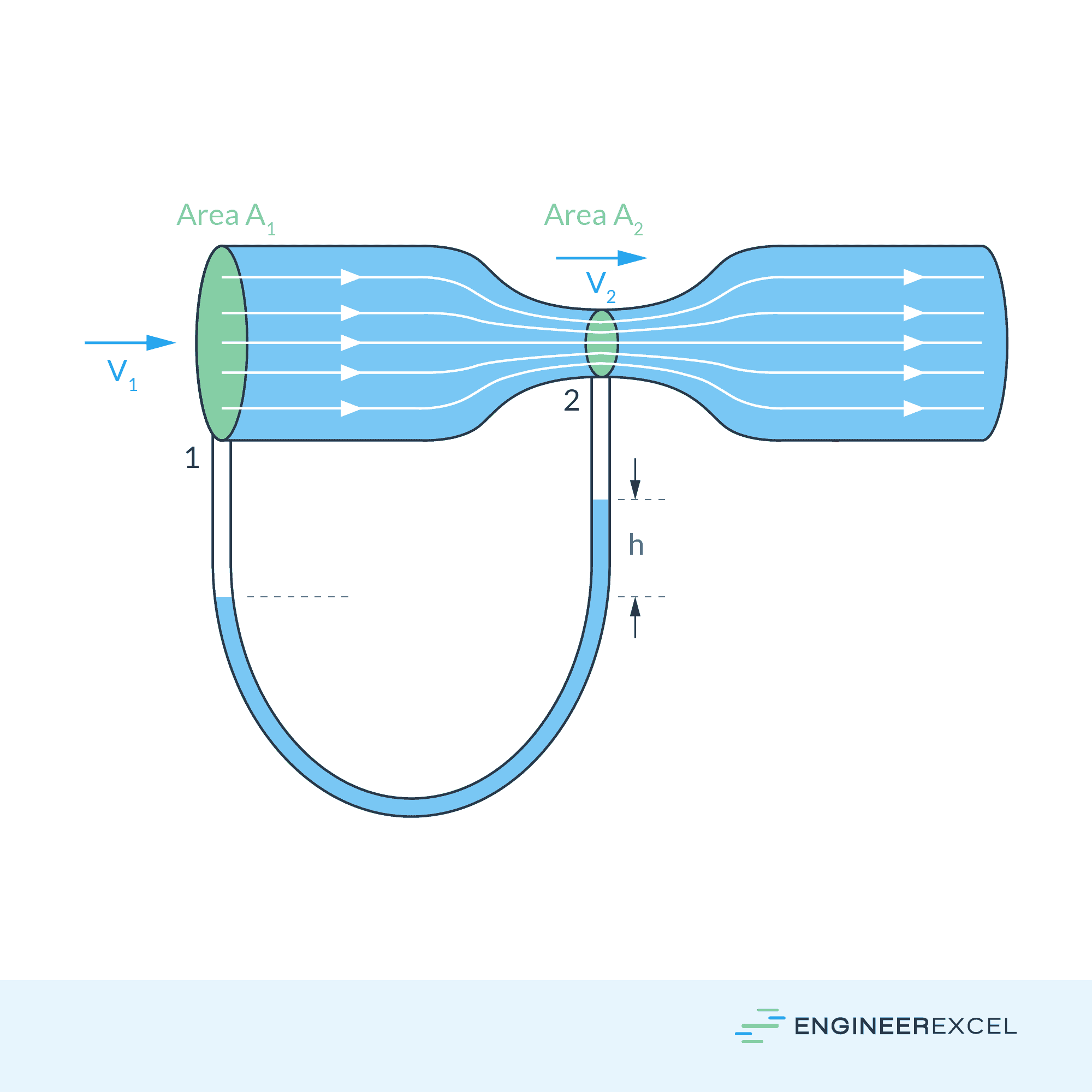
It follows that for two points lying on the same streamline, as shown in the diagram above, Bernoulli’s equation can be written as:
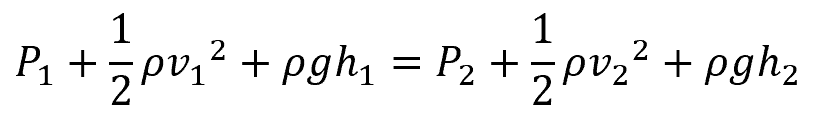
It is important to note that the above conditions follow the mass continuity or the conservation of mass equation. This means that for a steady flow, the rate of mass flow into a control volume equals the rate of mass flow out of the same control volume. Hence, fluid velocity increases as the cross-sectional area of the tube decreases, and vice versa.
For an incompressible fluid, this can be mathematically written as:
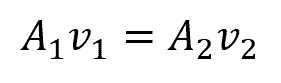
Where:
- A = cross-sectional area of the fluid tube [m2]
Applications of Bernoulli’s Equation
The Bernoulli equation is an essential tool for understanding the behavior of fluids and designing efficient fluid systems, particularly in aeronautics and hydraulics.
For example, it can be used to solve the flow rate of a fluid through a pipe or to determine the lift force on an airplane wing, which makes flying possible. It is also commonly utilized in the Venturi meter— a device that is used to measure the flow rate of fluids in pipes.
Lastly, carburetors use Bernoulli’s principle to regulate the fuel-air mixture entering the engine efficiently. As air enters the carburetor, it passes through a narrow tube called a venturi, which increases the air speed, causing the creation of a low-pressure area that draws in fuel from the jet. The resulting mixture is the air-fuel mixture, which flows into the engine, where it is ignited to produce power.
Poiseuille’s Law
Unlike Bernoulli’s equation, Poiseuille’s Law assumes a non-ideal fluid. This means that it considers the internal friction of the fluid when calculating the flow rate.
For a horizontal flow, as shown in the diagram below, what causes fluid motion is the difference in pressure. In general, fluid moves from higher to lower pressure. The greater the pressure difference, the higher the flow rate.

Poiseuille’s Law relates the flow rate of a viscous fluid to the pressure difference and fluid viscosity as well as to the radius and length of the tube through which the fluid is flowing.
Poiseuille’s Law Calculation
The horizontal flow of a viscous fluid due to pressure difference can be mathematically stated as:

Where:
- Q = volume flow rate [m3/s]
- P2 – P1 = pressure difference between the two ends [Pa or N/m2]
- R = resistance to flow [N-s/m5]
Note that this equation only applies to laminar flow— that is, fluid smoothly flowing in layers without mixing. Furthermore, the resistance to flow is dependent on the viscosity of the fluid as well as the length, size, and geometry of the tube.
For a viscous fluid flowing through a horizontal cylindrical tube, the resistance to flow can be mathematically written as:

Where:
- ƞ = viscosity of the fluid [Poise or N-s/m2]
- L = length of the tube or pipe [m]
- r = radius of the cylindrical tube or pipe [m]
Combining the two equations above, it follows that the flow rate through a horizontal cylindrical tube can be calculated using the formula:
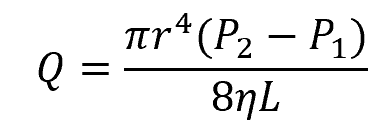
This equation is known as Poiseuille’s Law, named after the French scientist J. L. Poiseuille.
Applications of Poiseuille’s Law
Poiseuille’s Law is important in understanding the flow of viscous fluids in many biological and engineering systems.
In biomedical research, it is used to understand blood flow in small blood vessels and to measure blood pressure, which is important for diagnosing and treating heart diseases. Additionally, it is used to control the flow of fluids in microfluidic devices, which has applications in drug delivery and other areas of biomedical research.
In the oil industry, Poiseuille’s Law is also used to design oil pipelines and ensure efficient oil transportation. In the printing industry, it is used to control the flow of ink in inkjet printers, which allows for the production of high-quality prints with precise details.
