Static pressure is the pressure exerted by a fluid at rest, without any motion or flow. It is a measure of the potential energy stored in a fluid. In this article, we will discuss the concept of static pressure, including its calculation in liquids and gases as well as its applications in engineering.
Static Pressure Equation
Pressure is the result of a force distributed over an area, typically measured in units such as Pascals (Pa) or pounds per square inch (psi). There are different types of pressure depending on the context and the factors influencing it.
In fluid mechanics, static pressure is a type of pressure that refers to the pressure exerted by a fluid at rest. It is caused by the weight of the fluid and its value at a specific point is isotropic, meaning it is the same in all directions and acts perpendicular to surfaces, as illustrated in the diagram below.
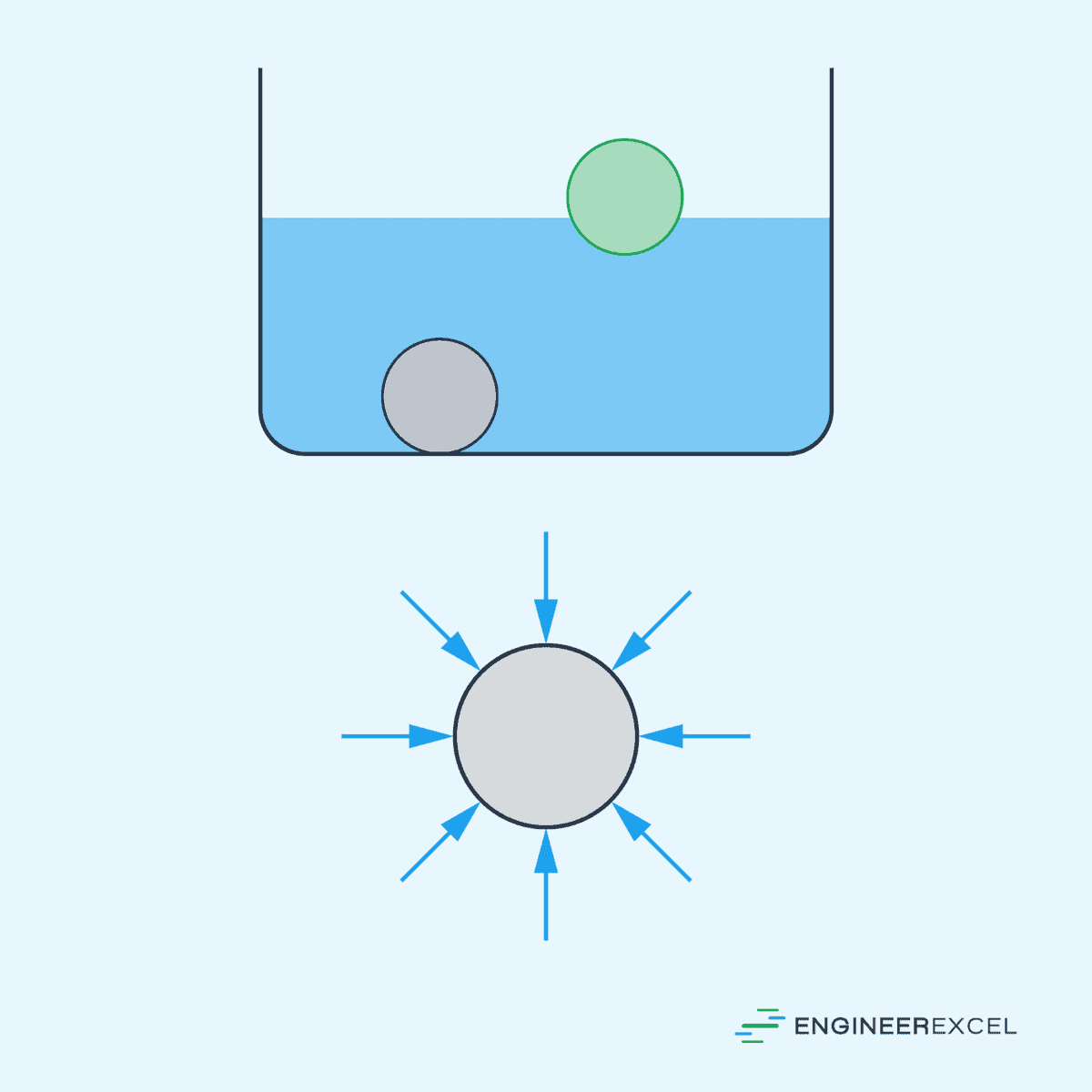
In a continuously distributed uniform static fluid, static pressure varies only with vertical distance and is independent of the shape of the container. This means that, for a given horizontal plane in the fluid, the pressure at all points is the same, and it only increases with depth.
Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
To illustrate, consider the diagram below.
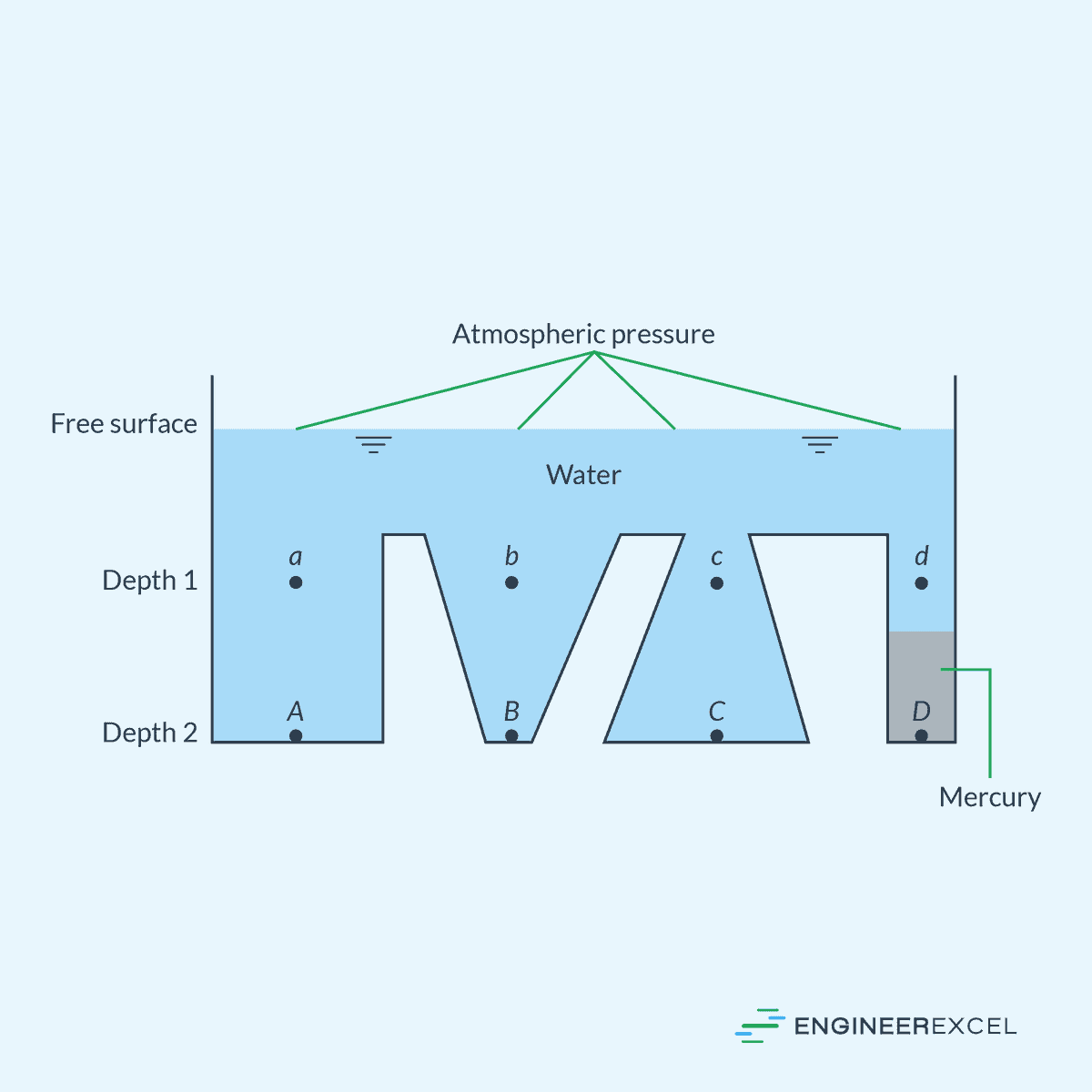
In the diagram, points a, b, c, and d share the same pressure as they are at equal depths in water. Likewise, points A, B, and C, being at equal depths, also share the same pressure, which is higher than that at a, b, c, and d. However, point D, despite having the same depth as A, B, and C, exhibits a different pressure.
This is because static pressure is also influenced by fluid density, as shown in the following equation:
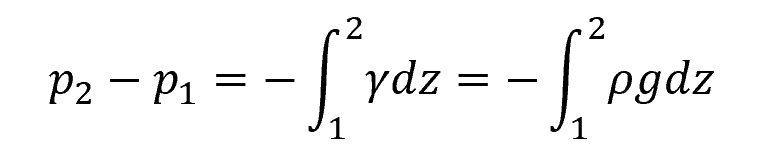
Where:
- p1 = pressure at the higher point [Pa]
- p2 = pressure at the lower point [Pa]
- γ = specific weight of the fluid [N/m3]
- ρ = density of the fluid [kg/m3]
- g = gravitational acceleration [9.81 m/s2]
- z = vertical distance from a reference plane, usually the free surface [m]
It is important to note that static pressure can be measured in two ways, depending on the point of reference: gauge pressure and absolute pressure. Gauge pressure is measured relative to atmospheric pressure, while absolute pressure is measured relative to a perfect vacuum.
Static Pressure Equation in Liquids
The solution for the above integral equation for static pressure is different for gases and liquids. For liquids, since they are nearly incompressible, the variation in density can be disregarded.
Hence, for a point below a liquid surface, the equation for static pressure can be reduced to:

Where:
- Pg = static pressure with respect to atmospheric pressure [Pa]
- h = vertical distance between the point and the liquid surface [m]
Note that this equation only calculates gauge pressure. To calculate absolute pressure, the atmospheric pressure must be added to the equation:

Where:
- Pa = absolute pressure [Pa]
- Patm = atmospheric pressure [Pa]
Static Pressure Equation for Gases
Gases are compressible, and their density is nearly proportional to pressure. Therefore, changes in density must be taken into account when calculating static pressure for gases, especially when the integration spans large pressure changes. We can use the perfect gas law to relate gas density to pressure:
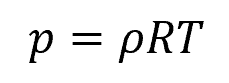
Where:
- p = gas pressure [Pa]
- R = gas constant [8.314 J/mol-K]
- T = gas temperature [K]
Assuming an isothermal atmosphere, the formula for static pressure then becomes:

Where:
- To = absolute sea-level temperature [K]
This equation provides a reasonable approximation for Earth, but in reality, the Earth’s average atmospheric temperature decreases almost linearly with z as described by the following equation:
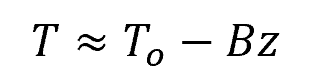
Where:
- B = lapse rate [K/m]
By international agreement, the absolute sea-level temperature is assumed to be equal to 288.16 K and the lapse rate is equal to 0.00650 K/m. However, in actual conditions, both of these values somewhat vary from day to day.
Applications of Static Pressure
In the field of fluid mechanics, static pressure plays a critical role in various instruments designed to gauge pressure levels. These devices are essential for accurate measurements in both scientific research and industry applications.
Barometers
Barometers are instruments that measure atmospheric pressure. They utilize the concept of static pressure to provide readings that aid in weather forecasting and altitude determination.

Mercury barometers consist of a glass tube inverted in a mercury bath; as atmospheric pressure changes, the mercury level rises or falls, corresponding to the static pressure exerted by the air. Aneroid barometers, on the other hand, use a small, flexible metal box called an aneroid cell, which expands or contracts with changes in atmospheric pressure. These devices translate the mechanical movement into a static pressure reading.
Manometers
Manometers measure the static pressure of a fluid within a system relative to atmospheric pressure or another reference pressure. They function by balancing the fluid of known density against the pressure to be measured. Manometers come in various types, such as:
- U-tube Manometers: These are the simplest form, consisting of a U-shaped tube with a known fluid like mercury. The difference in fluid level between the two arms of the tube correlates with the static pressure difference.
- Inclined Manometers: Often used for more sensitive measurements, inclined manometers have a tube positioned at a slight angle to increase the measurement’s resolution.
Understanding static pressure is essential for designing and analyzing fluid flow systems, such as pipelines, ducts, and ventilation systems. It is particularly vital in HVAC applications, where maintaining a specific static pressure ensures proper airflow and distribution. Additionally, static pressure is integral in aerodynamics, providing insights into aircraft and vehicle design, as well as in hydraulic systems, aiding in the efficient operation of pumps and turbines.
