Flexural strength is the maximum stress that a material can withstand before it breaks when subjected to bending. It is typically determined through a standardized testing procedure that involves subjecting a specimen to a bending test. In this article, we will discuss the factors affecting flexural strength, the different types of flexural tests, and the standards for flexural strength testing.
What is Flexural Strength?
Flexural strength is a measure of a material’s ability to resist deformation under bending loads. It is an essential property to consider in materials used for structural applications, as it provides an indication of the material’s resistance to failure when subjected to bending forces.
When a specimen is bent, it undergoes different levels of normal stress throughout its depth, as shown in the diagram below. The highest compressive stress occurs at the edge of the concave face of the specimen. On the other hand, the maximum tensile stress occurs at point B, which is the convex face of the specimen.
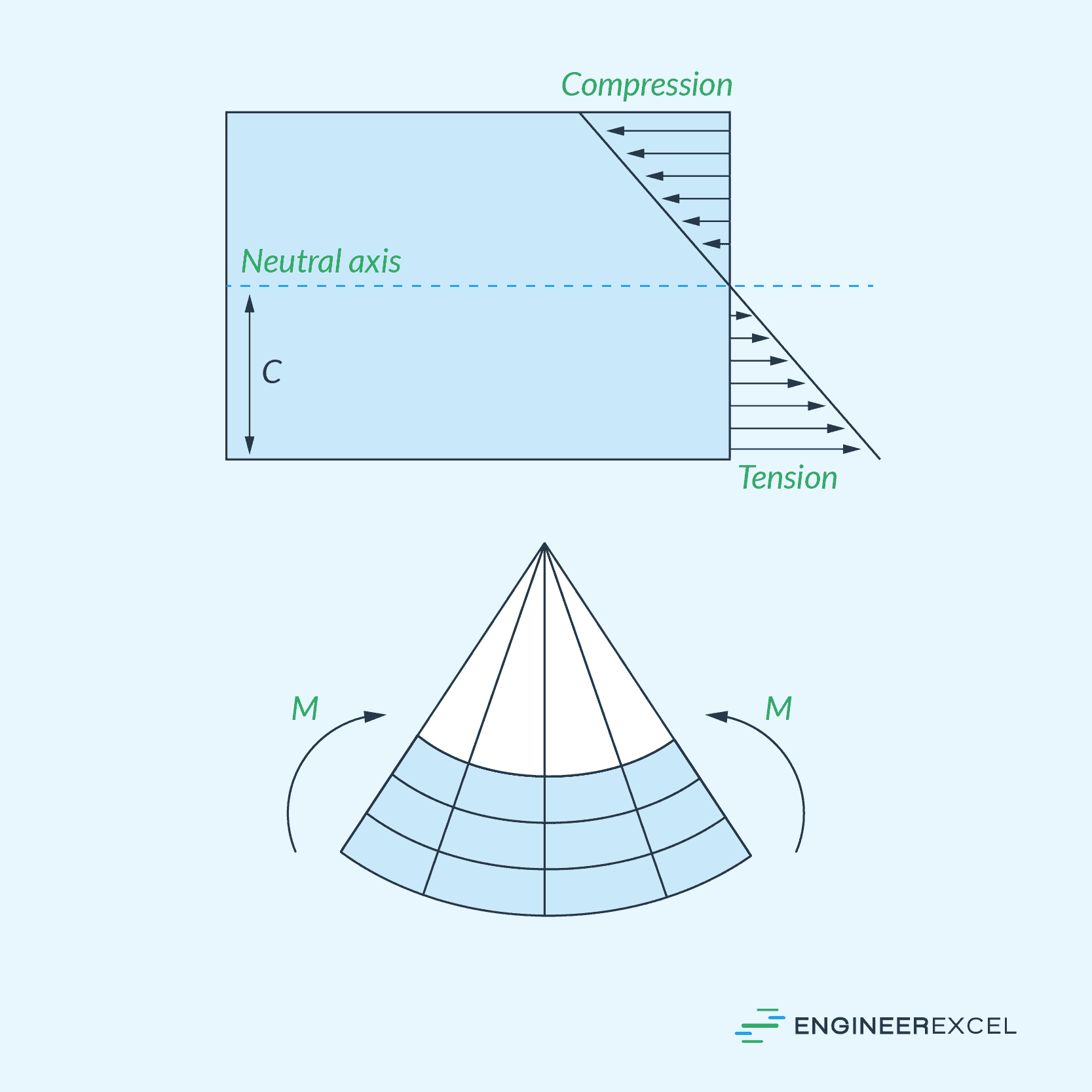
Materials typically fail under tensile stress before they fail under compressive stress, so the flexural strength is usually determined by the maximum tensile stress it can withstand before it breaks. Hence, if the material composition were homogeneous, its flexural strength would be the same as its tensile strength.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
However, this is not true for most structures. Structural components normally have a complex structure and small defects that concentrate stresses locally, resulting in weaker areas and lower flexural strength values.
The flexural strength of a material is determined through a standardized testing procedure that involves subjecting a specimen to a bending test. In this test, a force is applied at specific points along the length of the specimen until it fractures or exhibits significant deformation. The flexural strength is expressed in units of stress, usually in megapascals or pounds per square inch, and represents the maximum stress the material can withstand in bending without failing.
Flexural strength is essential for assessing the suitability of materials for specific applications. This is particularly important in designing reinforced concrete structures like bridges and buildings. Similarly, in the aerospace industry, the flexural strength of materials used in aircraft components is essential to ensure structural integrity under various operational conditions.
Factors Affecting Flexural Strength
Various factors influence flexural strength, including the material’s composition, distribution of the reinforcement, environmental conditions, and loading conditions.
Material Type
Different materials exhibit different flexural strengths, often attributed to their inherent properties.
For instance, concrete has a lower flexural strength when compared to steel, due to its lower tensile capacity. Conversely, steel has a high tensile capacity, which leads to a higher flexural strength. Fiber-reinforced polymers, being anisotropic in nature, have different flexural strengths in different directions.
Reinforcement Distribution
The presence, type, and distribution of reinforcement can significantly impact the flexural strength of a material. Reinforced masonry design, for instance, considers the area of tensile reinforcement, as well as the axial and flexural strength interaction. Similarly, in steel-reinforced concrete beams, the position and amount of steel reinforcement directly influence the flexural capacity.
Environmental Conditions
The flexural strength of a material can be affected by environmental factors such as temperature, moisture, and even exposure to aggressive chemicals. For example, temperature fluctuations can induce shrinkage or expansion in materials like concrete, reducing their overall flexural strength. Similarly, exposure to moisture and aggressive chemicals can lead to corrosion of steel reinforcement in concrete, ultimately weakening the flexural strength of the structure.
Loading Conditions
The manner in which a load is applied, such as a point load or a distributed load, can influence the material’s flexural strength. Static and dynamic loads can also have varying effects on the overall flexural capacity. In addition, the rate at which the load is applied might lead to different outcomes, as materials may exhibit an increased flexural resistance under a gradually applied load as compared to a sudden, impact load.
Flexural Strength Testing Methods
There are two common types of flexural tests: three-point and four-point flexural loading tests. During these tests, a material sample is subjected to a controlled bending force, and the flexural strength is calculated based on the maximum stress experienced by the material prior to its failure.
Three-Point Bending Test
In the three-point bending test, a beam is supported at two points and a force is applied at the midpoint. The flexural strength can be calculated by measuring the maximum tensile stress that occurs on the lower fiber of the beam at peak load.
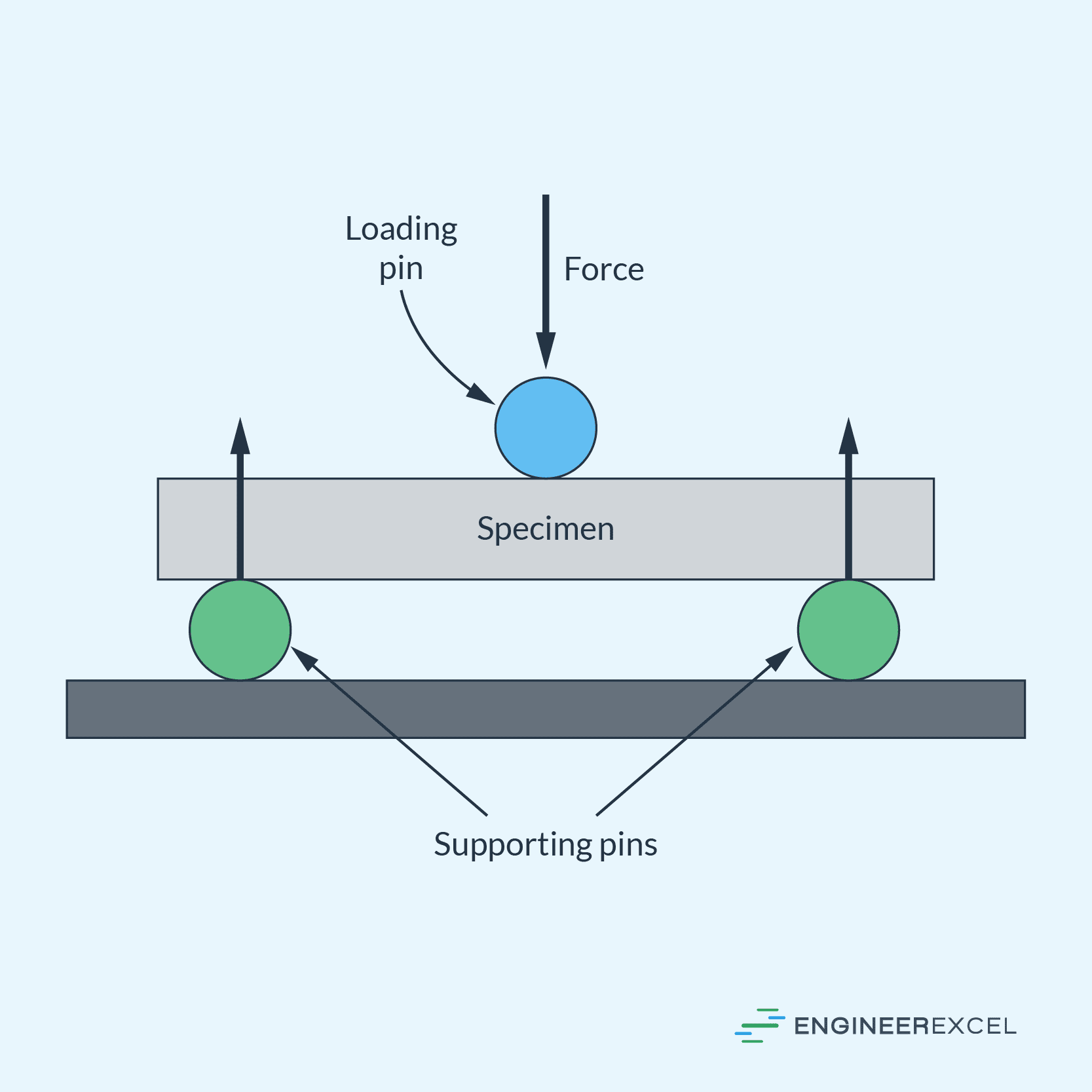
The primary advantage of the three-point bending test is its simplicity and ease of setup. However, one limitation is the potential for uneven stress distribution throughout the specimen, which may lead to premature failure.
For a rectangular beam, the flexural strength using the three-point bending test can be calculated using the following formula:

Where:
- σf = flexural strength [Pa]
- P = peak applied force at the midpoint [N]
- L = span between the supports [m]
- b = beam width [m]
- h = beam height [m]
For a cylindrical beam:
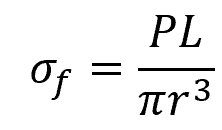
Where:
- r = beam radius [m]
Four-Point Bending Test
The four-point bending test is almost similar to the three-point test but involves two loading points instead of one. These loading points are symmetrically positioned along the beam, which leads to a more even stress distribution across the test specimen.
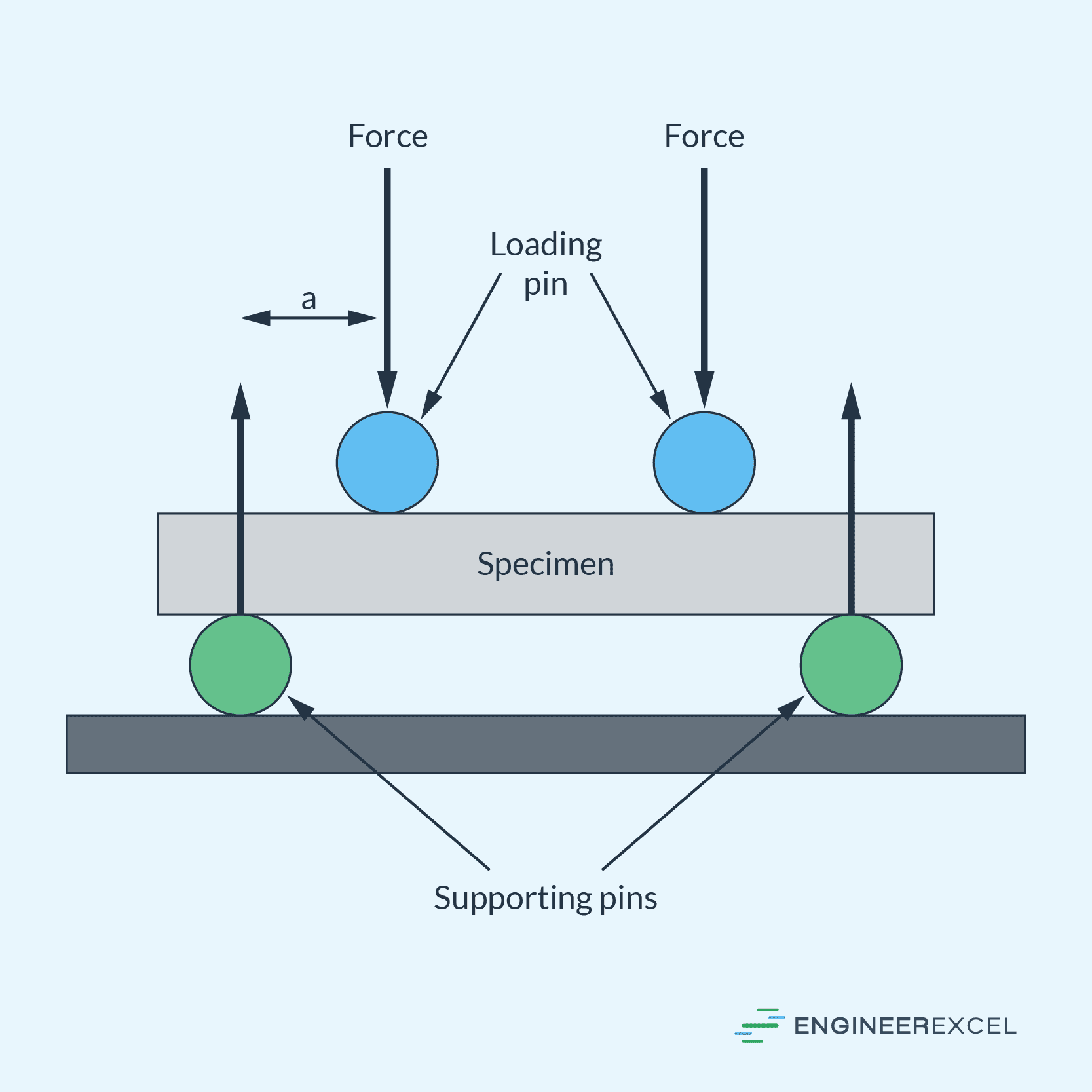
For a rectangular beam, the calculation for flexural strength in the four-point bending test depends on the loading span. If the loading span is one-half of the support span, the flexural strength can be calculated using the following formula:
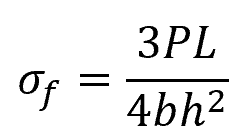
If the loading span is one-third of the support span:
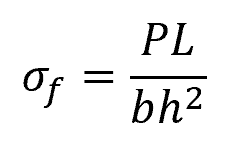
While the three-point bending test is simpler, the four-point bending test provides better control over stress distribution and is more suited for situations where accurate measurements are important.
Standards for Flexural Strength Testing
The American Society for Testing and Materials (ASTM) has published several standards related to flexural strength testing, including ASTM C78 for concrete, ASTM D790 for plastic materials, and ASTM C293 for ceramic materials. These standards outline the equipment requirements, sample preparation procedures, and calculation methods necessary to obtain accurate and reproducible results.
When conducting flexural strength tests, it is important to follow the appropriate test procedures and guidelines in order to obtain accurate and comparable results. Factors such as sample geometry, loading rate, and support span can significantly impact the outcomes of the test and must be carefully controlled according to the relevant standard.
