The Reynolds number is a dimensionless quantity that represents the ratio of inertial forces to viscous forces within a fluid. It plays a crucial role in fluid dynamics by helping describe the behavior of fluid flow and providing valuable insights into the different flow regimes. This article aims to explore the concept of the Reynolds number, its significance, applications, and how it is calculated.
Reynolds Number And What It Represents
Reynolds number, named after Osborne Reynolds, is a dimensionless quantity that describes the viscous behavior of a moving fluid. In fluid mechanics, it helps predict the behavioral pattern of fluid flow by measuring the ratio between inertial and viscous forces, as illustrated by the following equation:
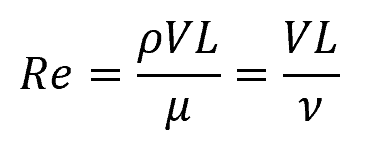
Where:
- Re = Reynolds number [unitless]
- ρ = density of the fluid [kg/m3]
- V = velocity of the fluid [m/s]
- L = characteristic length of the flow [m]
- μ = dynamic viscosity of the fluid [Pa-s]
- ν = kinematic viscosity of the fluid [m2/s]

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
As shown in the equation above, the Reynolds number is dependent not only on the characteristics of the moving fluid but also on the medium through which it flows.
The characteristic length of the flow depends on the situation. For instance, for fluids flowing in a pipe, the characteristic length can be the pipe diameter. On the other hand, in the case of a flat plate, it can be the length of the plate perpendicular to the flow.
Note that the equation for Reynolds number mentioned above is specifically applicable to Newtonian fluids such as air and water. In these fluids, the shear stress is directly proportional to the shear strain rate, following Newton’s law of viscosity. According to this law, the shear stress between adjacent fluid layers is proportional to the negative of the velocity gradient across the direction perpendicular to the flow, as shown in the following equation:
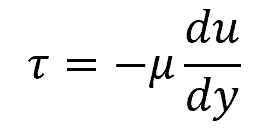
Where:
- τ = shear stress between adjacent fluid layers [Pa]
- du/dy = fluid velocity gradient [s-1]
However, there exist fluids that do not obey this law, known as non-Newtonian fluids. Examples of non-Newtonian fluids include slurries, polymer solutions, blood, paste, and colloidal suspensions. Unlike Newtonian fluids, the viscosity of non-Newtonian fluids is not constant and can vary based on the shear rate or applied stress.
These fluids exhibit different flow behaviors under different conditions, which makes their viscosity more complex to characterize. To account for non-Newtonian fluids, Metzner and Reed proposed a generalized formula for the Reynolds number in fluid flow through pipes, which can be mathematically expressed as:
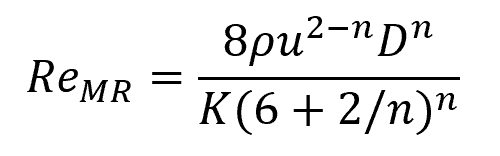
Where:
- ReMR = Metzner-Reed Reynolds number [unitless]
- u = fluid velocity [m/s]
- D = pipe internal diameter [m]
- K = flow consistency index [Pa-sn]
- n = flow behavior index [unitless]
The flow consistency index (K) is an average viscosity measure for non-Newtonian fluids. As the fluid becomes more viscous, the flow consistency index increases, and vice versa.
The flow behavior index (n), on the other hand, characterizes the relationship between fluid viscosity and strain rate. For shear thinning fluids, which become less viscous as the shear rate increases, the value of n is between 0 and 1.
In the case of Newtonian fluids, the flow behavior index is 1, indicating a linear relationship between viscosity and shear rate. Furthermore, the flow consistency index is equivalent to the dynamic viscosity of the fluid, allowing the Metzner-Reed equation to be simplified into the standard equation for Reynolds number.
There are other models used to characterize the Reynolds number for non-Newtonian fluids. However, for the sake of this article, the focus will be on Newtonian fluids.
High vs Low Reynolds Number
In general, the first task of a fluids engineer is to estimate the range of the Reynolds number for the flow under investigation. Assessing the Reynolds number provides valuable insights into the flow characteristics and helps determine the dominant type of motion.

When the Reynolds number is very low, it signifies a regime of viscous creeping motion, where the effects of inertia are negligible. At these low values, the flow is primarily dominated by laminar motion, resembling thin, sheet-like layers of moving fluid. Because of relatively high viscosity, small natural disturbances within the flow damp quickly.
In contrast, at sufficiently large Reynolds numbers, the flow will fluctuate continually, resulting in turbulence. This turbulence occurs due to variations in the fluid’s speed and direction, leading to the formation of eddy currents that can intersect or counter the overall flow direction. These fluctuations, which typically range from 1 to 20 percent of the average velocity, are not strictly periodic; instead, they are random and encompass a continuous range of frequencies.
When the Reynolds number is moderate, the flow exhibits a combination of laminar and turbulent patterns. This results in a steady appearance on average with occasional sharp bursts of intermittent fluctuations as the increasing Reynolds number causes a breakdown or instability of laminar motion. This type of flow is harder to characterize because the location and timing of transition between laminar and turbulent flow occurs randomly.
Reynolds Number At Different Flow Regimes
Flow regimes are characterized by distinct flow characteristics, including the velocity profile, pressure distribution, and overall behavior of the fluid. In general, flow can be divided into three regimes: laminar flow at low Reynolds numbers, transition at intermediate Reynolds numbers, and turbulent flow at high Reynolds numbers.

Determining the exact value of the Reynolds number at which the shift between flow regimes occurs is challenging and heavily depends on the specific geometry of the flow and the characteristics of the fluid. As a result, it is difficult to provide explicit thresholds for low, moderate, or high Reynolds numbers. However, these ranges of Reynolds numbers can be estimated through experiments.
Reynolds Number For Laminar Flow
The laminar flow regime generally occurs at Reynolds numbers ranging from 0 to 103. At Reynolds numbers between 0 and 1, the flow is highly viscous and characterized by a creeping motion. Between 1 and 102, the flow is still very much laminar and strongly dependent on the Reynolds number.
When fluid flows over a solid object in the range of 102 to 103 Reynolds numbers, the molecules in the fluid interact with the surface, resulting in the formation of a thin layer of fluid adjacent to the solid surface. At this range, it is necessary to use boundary layer theory to characterize the flow.
Reynolds Number For Transitional Flow
The transition region between laminar and turbulent flows occurs in the range of 103 and 104. Engineers generally avoid designing flow operations in this region because of its unpredictable nature.

For pipe flows specifically, the accepted critical range of Reynolds numbers at which the flow transitions from laminar to turbulent is from 2300 to 4000. It is important to note that this range is only applicable to pipe flows; other geometries like plates and airfoils have entirely different transition Reynolds numbers.
Reynolds Number For Turbulent Flow
Generally, the turbulent flow regime occurs at Reynolds numbers in the range of 104 and above. Within the range of Reynolds numbers between 104 and 106, the flow characteristics are still moderately influenced by the value of the Reynolds number. However, beyond this range, the viscosity diminishes, and the flow characteristics become almost independent of the Reynolds number.
Unlike laminar flow, simulating the fine-scale random fluctuations of turbulent flow is challenging. As a result, most turbulent flow theory is semiempirical, relying on dimensional analysis and physical reasoning. It primarily focuses on the mean flow properties rather than the specific rapid variations.
Applications Of Reynolds Number
Reynolds number is generally considered to be the most important parameter in fluid mechanics as it helps analyze and predict the behavior of fluid flow in different situations. By determining whether the flow is laminar or turbulent, engineers can choose the appropriate analysis models and methods required for designing and optimizing fluid systems.

In piping systems, for example, Reynolds number is closely related to friction factor, which plays a vital role in calculating the pressure loss. In laminar flow, the friction factor decreases inversely with the Reynolds number. On the other hand, in turbulent flow, the friction factor is influenced by both the Reynolds number and pipe roughness.
In similarity analysis, Reynolds number is also one of the key dimensionless parameters that help determine the dynamic similarity of two fluid systems, together with Mach, Prandtl, Froude, Euler, Grashof, and Weber numbers. When two systems have the same Reynolds number, they are expected to exhibit similar flow patterns and behavior, regardless of their size or velocity. This allows engineers to scale experiments or simulations from a small-scale model to a larger system.
In the context of heat transfer, Reynolds number significantly affects the convective heat transfer coefficient, which governs the rate at which heat is transferred between a solid surface and a fluid. For low Reynolds numbers, heat transfer is primarily dominated by conduction and heat is primarily transferred through molecular diffusion. Conversely, for high Reynolds numbers, heat transfer is enhanced due to increased mixing and fluid agitation.
