In open channel flows, the best hydraulic cross section refers to a geometric configuration of a channel that maximizes flow efficiency, ensuring optimal hydraulic performance. It is characterized by a balance between depth, width, and slope to achieve the most efficient conveyance of water with minimal energy loss.

In this article, we will discuss the critical factors that determine the best hydraulic cross-section, the equations used in the analysis of open channel flows, and the best hydraulic dimensions for common open channel cross-sectional shapes.
Best Hydraulic Cross Section Explained
Open channel flow refers to the flow of water in a natural or artificial channel with a free water surface, such as rivers, streams, or drainage channels. In the context of open channel flows, the term best hydraulic cross section refers to the most efficient shape of an open channel.
Two critical factors determine the best hydraulic cross-section: maximizing the flow rate in order to reduce flooding risk, and minimizing the cross-sectional area and the minimum lining area in order to minimize construction and maintenance costs.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
In the analysis of open channel flows, two equations are typically used to determine the best hydraulic cross -section: the continuity equation and the Manning’s equation.
The continuity equation is a fundamental principle that states that the product of the flow area and the flow velocity must be equal to the flow rate or discharge. Mathematically, this can be expressed as:
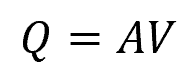
Where:
- Q = discharge [m3/s]
- A = cross-sectional area of the flow [m2]
- V = flow velocity [m/s]
On the other hand, Manning’s velocity equation is an empirical equation that is widely used to predict the flow velocity in open channel flows. In SI units, it can be represented as:
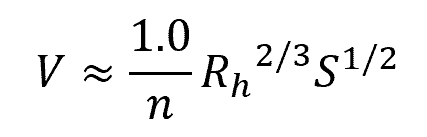
Where:
- V = fluid velocity [m/s]
- n = Manning roughness coefficient [unitless]
- Rh = hydraulic radius [m]
- S = slope of the channel [unitless]
In English units, it can be expressed as:
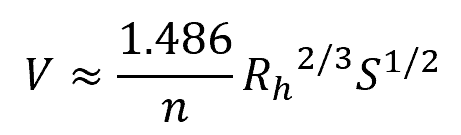
Where:
- V = fluid velocity [ft/s]
- Rh = hydraulic radius [ft]
From the continuity equation, we can see that in order to maximize flow rate and minimize cross-sectional area, we should maximize flow velocity. Consequently, from the Manning’s equation, in order to maximize flow velocity, we should maximize the hydraulic radius.
Note that hydraulic radius is defined as:
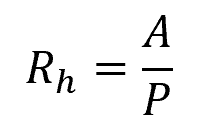
Where:
- P = wetted perimeter [m]
Hence, in order to optimize open channel flows, we should ultimately minimize the wetted perimeter.
Best Hydraulic Cross-Sectional Dimensions of Different Shapes
Open channel flows can have different cross-sectional shapes, which play a significant role in determining the flow characteristics. In this section, we’ll discuss the best hydraulic dimensions for some of the most common open channel cross-sectional shapes.
Rectangular Cross-Section
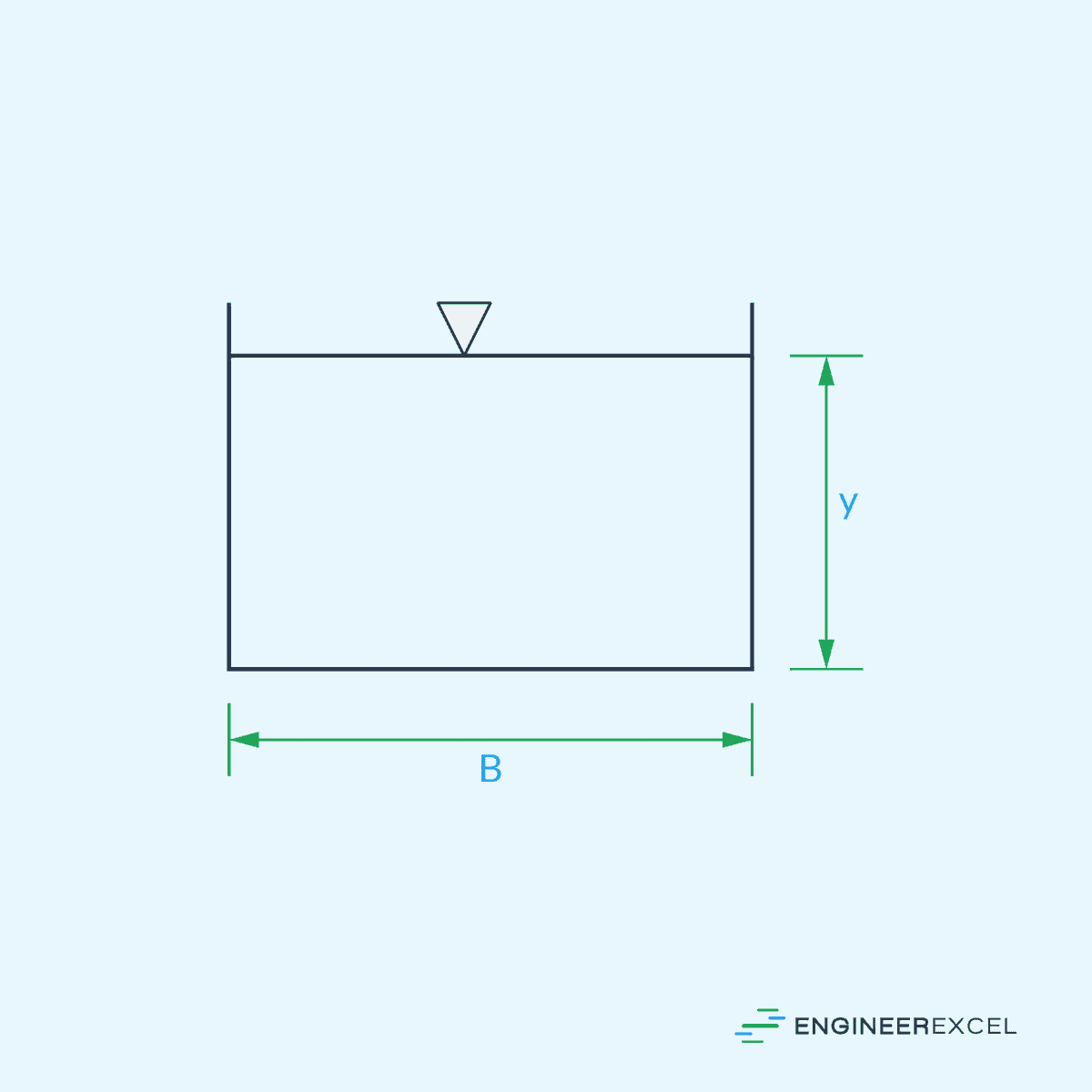
For a rectangular open channel, shown above, the minimum wetted perimeter can be achieved if:
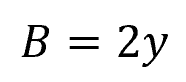
Where:
- B = base of the rectangle [m]
- y = depth of the flow [m]
For this cross-section, the hydraulic radius is equal to:
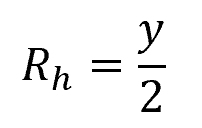
The cross-sectional area is equal to:
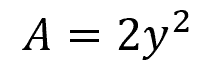
And the wetted perimeter is equal to:
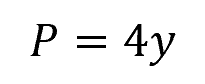
Trapezoidal Cross-Section
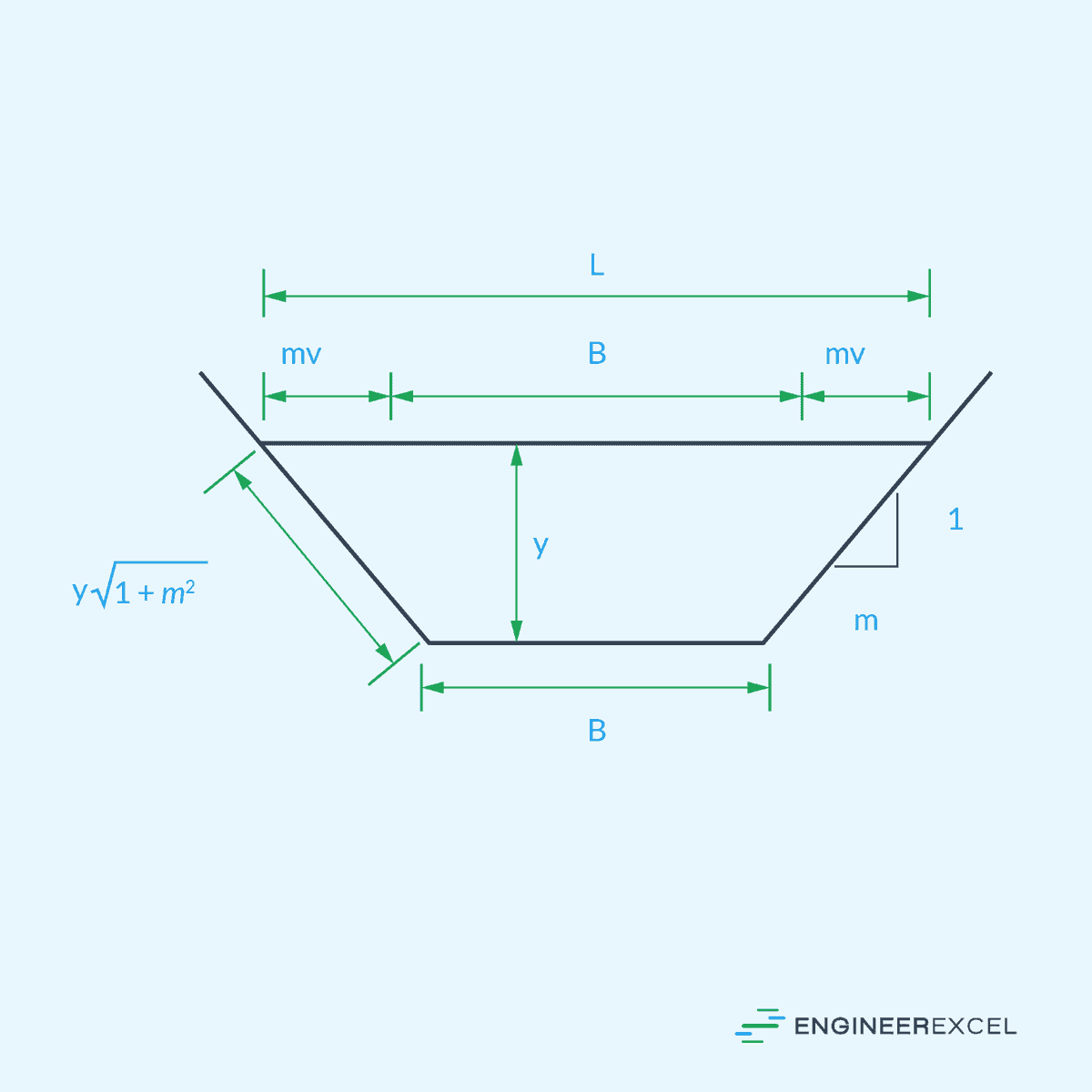
For a trapezoidal open channel, shown above, the minimum wetted perimeter can be achieved if:
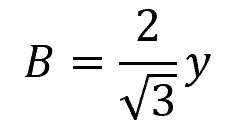
Where:
- B = base of the trapezoid [m]
Then the width of the water surface is equal to:
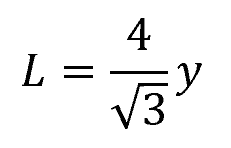
The hydraulic radius is equal to:

The cross-sectional area is equal to:
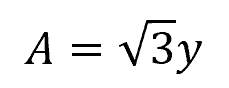
And the wetted perimeter is equal to:
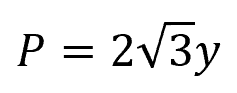
Semi-Circular Conduit
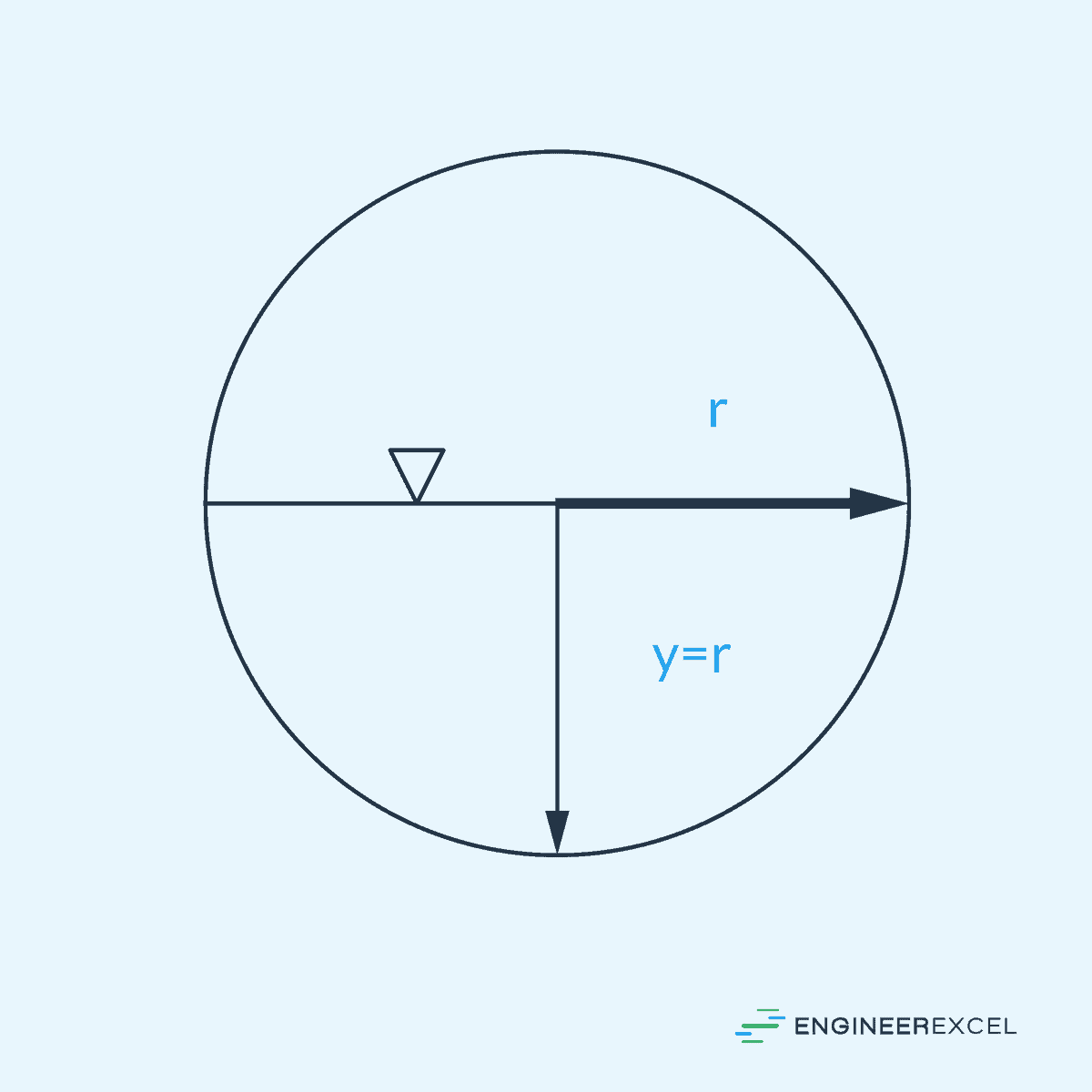
A semi-circular conduit itself is a best hydraulic cross-section. In this case, the width of the water surface is equal to:
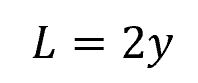
The hydraulic radius is equal to:
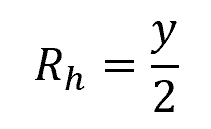
The cross-sectional area is equal to:

And the wetted perimeter is equal to:
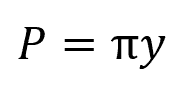
Triangular Cross-Section
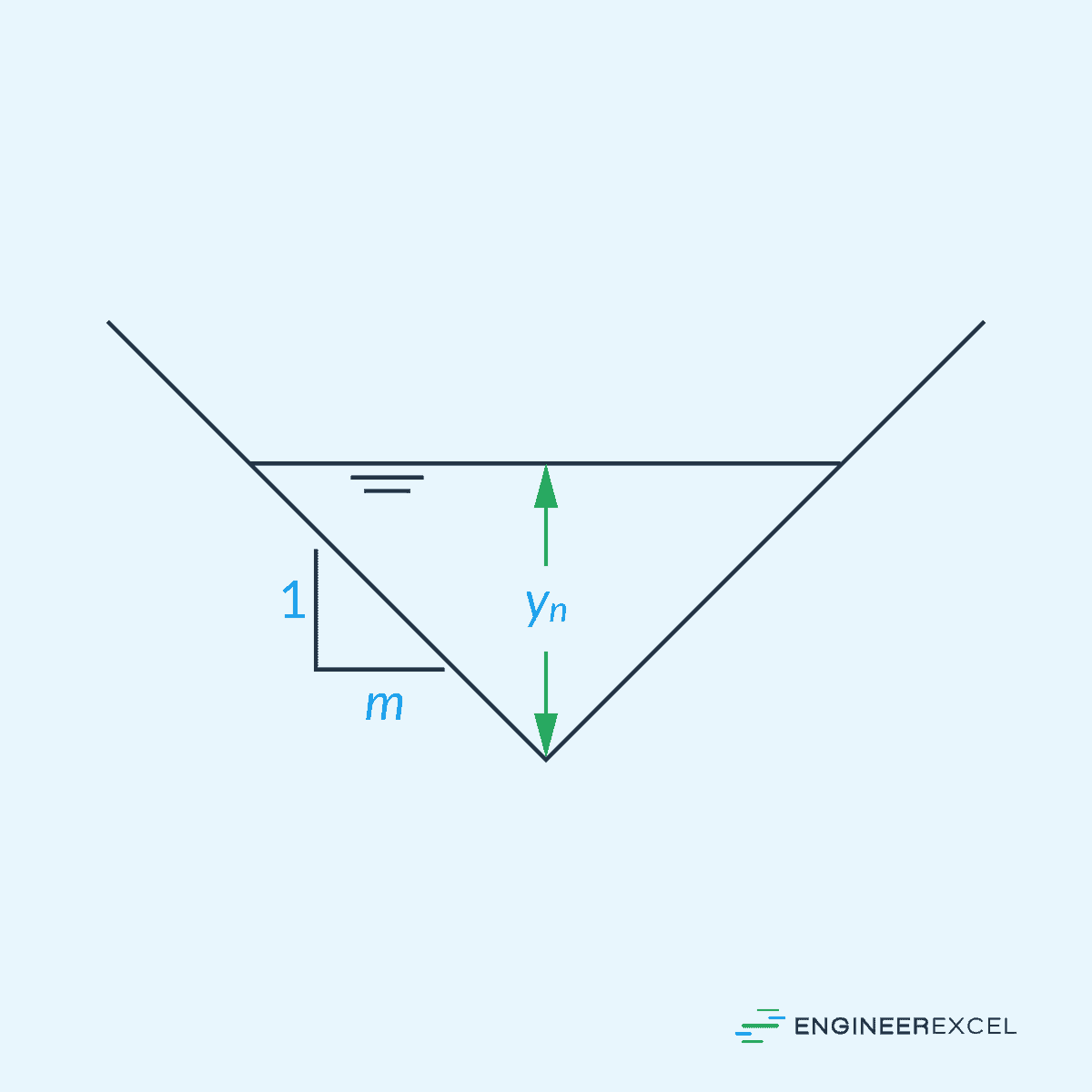
For a triangular channel, the best hydraulic cross-section is one with a side slope of 1:1. In other words, the vertex of the triangle should be 90°.
In this case, the width of the water surface is equal to:
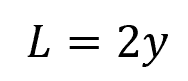
The hydraulic radius is equal to:
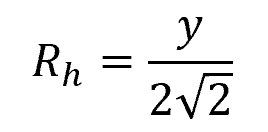
The cross-sectional area is equal to:
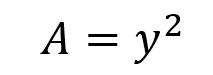
And the wetted perimeter is equal to:
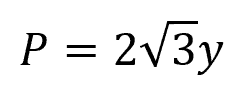
Real-World Applications
Open channel flows have numerous applications across various engineering and environmental fields. In civil engineering, open channels are used to control and manage stormwater runoff in urban areas, helping to prevent flooding and erosion. They are also employed in the design of irrigation canals, drainage channels, and navigation canals for water distribution and transportation.
In environmental engineering, open channel flow principles are important in studying and managing rivers and streams for purposes such as flood control, water supply, and habitat preservation. They are also used in wastewater treatment plants for various processes, such as sedimentation and aeration.
Selecting an efficient hydraulic cross-section for these applications is important as it directly affects flow characteristics and performance of the system. In general, the selected cross-section should efficiently transport the expected volume of water without causing excessive flow velocities or erosion.
Well-designed cross-sections should also promote uniform flow, reducing the likelihood of turbulence, eddies, or excessive sedimentation. By minimizing these hydraulic irregularities, the risk of erosion and sedimentation within the channel is reduced, ensuring the long-term integrity and functionality of the infrastructure.
When it comes to canals and stormwater drains, selecting the best hydraulic cross-section is influenced by factors such as the surrounding topography and expected variability in flow rates. Different cross-sections may be suitable for accommodating steady flows, flood events, or variations in water levels.
Additionally, cost-effectiveness and sustainability are important considerations in the design process. The chosen hydraulic cross-section should not only meet hydraulic performance criteria but should also be economically viable to construct and maintain.
