In engineering applications, steady state systems are idealized closed control volumes that do not change with time. Such a state is considered idealized because it is used for practical engineering applications without the need to consider the minute details that a real system will be subject to. To apply the results of a system design assuming steady state, a margin will be applied to the final results.
Definition Of A Steady State System
A steady state system is one in which the mass and energy of the control volume does not change and the properties at any point within the volume do not depend on the time. In other words, if the state of the system is measured at any time, that state will be the same if measured at some other time. A steady state system will maintain an overall more ordered condition than the environment in which it exists. As most systems tend toward a state of higher entropy (disorder), the very nature of a steady state system means that it will always maintain the same level of entropy over time.
A steady state system may also be referred to as being in dynamic equilibrium, although steady state is a more general term. A system defined to be in homeostasis can also be considered to be in a steady state, although homeostasis is a term that refers to an entire environment, whereas steady state is a term that refers to specific mechanisms within an environment.
Examples Of A Steady State System
There are various types of systems that can be in a steady state. These different systems are applicable to different types of engineering, but they are all systems in which the state does not vary over time.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
Thermodynamics
In thermodynamics, a steady state system will be one in which the energy flowing into the system is exactly equal to the energy flowing out of the system. Consequently, the state within the control volume that defines the system will not change. Such a system represents the conservation of energy within a closed system. An example of such a system is shown in the following figure:
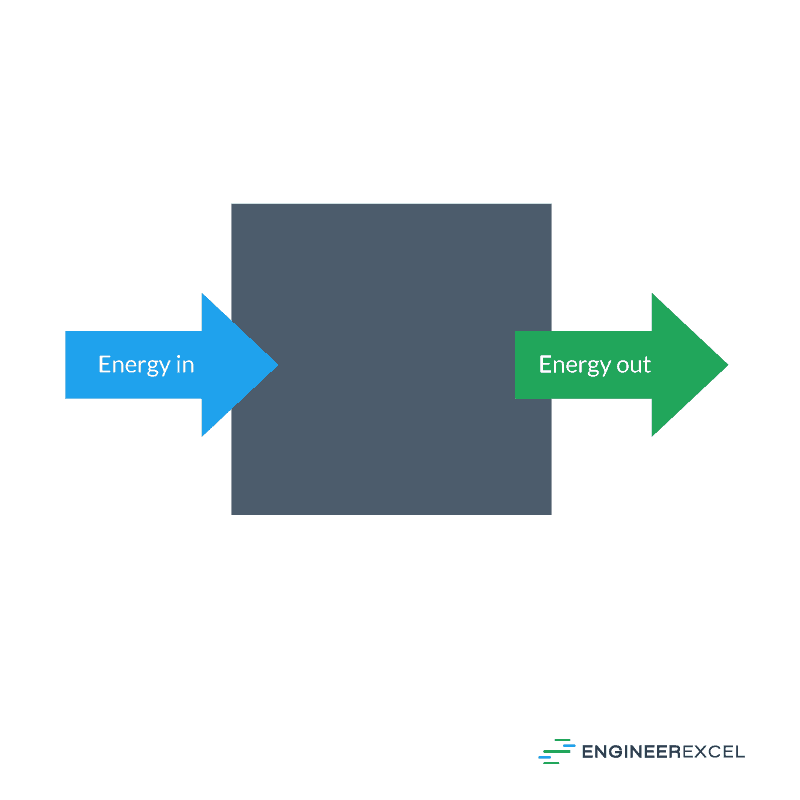
In a thermodynamic system, the steady state is defined via the following equation:
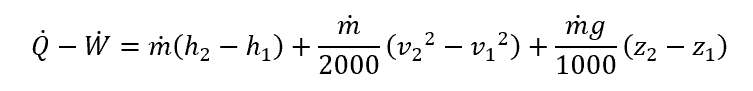
where:
- Q̇ is the heat transfer, with units of kJ
- Ẇ is the work transfer, with units of kJ
- ṁ is the mass flow rate, with units of kg/s
- h is the specific enthalpy, with units of kJ/kg
- v is the velocity, with units of m/s
- g is the gravitational constant, equal to 9.81 m/s2
- z is the height, with units of m
In the above, the subscripts indicate the first and second states.
An example of a thermodynamic system exhibiting steady state properties would be a turbine in which heat energy in the form of steam flows into the system and work energy is output from the system, but the state within the control volume enclosing the turbine does not change.

Chemistry
In a chemical system, such as a flask containing pure water sitting at room temperature, so long as no energy is being input to the system, the balance of ions in the flask will remain constant. If something is added to the flask, the system will no longer be steady state, but will tend toward such a state, and eventually reach it.
Using the same flask of pure water as an example, the steady state can be defined by the following:
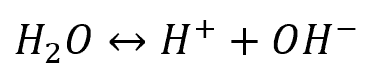
In this system, the water transitions into H+ and OH– ions and those ions transition back into water at the same rate.

Mechanical Or Structural
In mechanical or structural engineering, a steady state system will be one in which the mass of the system does not change over time. This principle is applicable to the conservation of mass in a system, and can be visualized in the following figure:
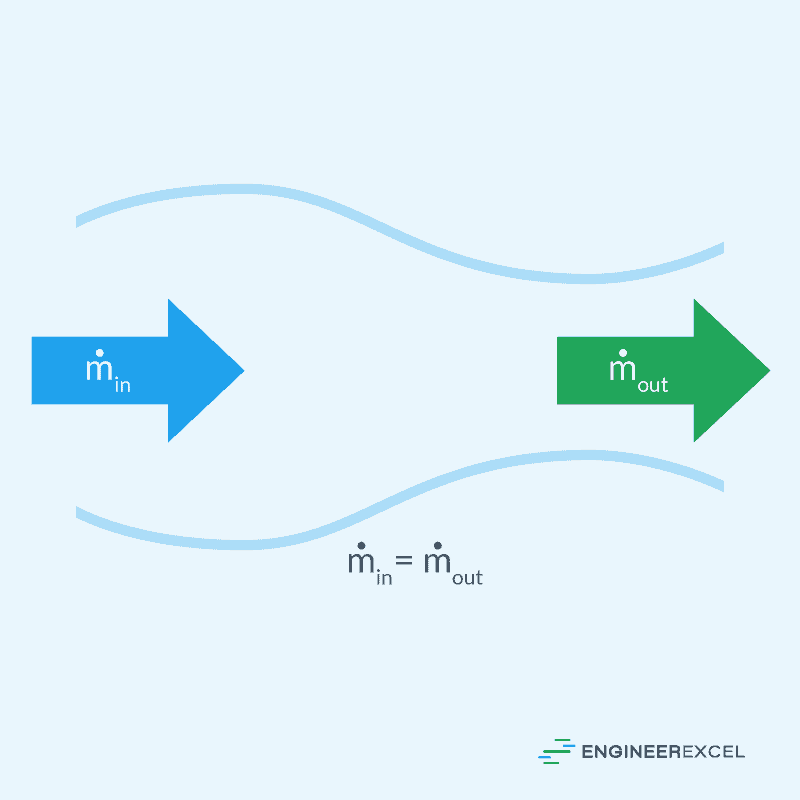
Fluid Mechanics
Similar to a system involving mass, in fluid dynamics a steady state system will be one in which the flow of a fluid (liquid or gas) into the system is equal to the flow out of the system.
A steady state system in fluid mechanics can be represented by the flow of air through a nozzle. In such a system, the flow of mass (air) will be the same going into the system as the flow leaving the system. In
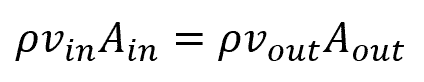
where:
- ρ is the density of the fluid, with units of kg/m3
- v is the velocity of the fluid at the inlet or outlet, with units of m/s
- A is the area of the inlet or outlet, with units of m2
Assuming incompressible flow, such that the density remains constant, the relationship between the inlet parameters and the outlet parameters is as follows:
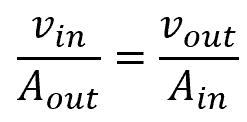
From the above equation, the inlet velocity and area are inversely proportional, as are the outlet velocity and area. Therefore, to maintain a steady state system, an outlet area smaller than the inlet area will result in an outlet velocity larger than the inlet velocity.
