Understanding the transfer of energy between matters is essential in the design and analysis of different types of systems. Energy exists in diverse forms, such as electrical, thermal, mechanical, chemical, motion, radiant, and gravitational; hence, there are multiple approaches to modeling and quantifying energy transfer.
This article examines various methods for calculating energy transfer in some of the most common physical scenarios.
Energy Transfer Calculation
Energy, in its broadest sense, refers to the inherent capacity of an object or system to perform work. It exists in various forms and can be converted from one form to another.
It can be broadly classified into two categories: potential energy and kinetic energy.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
Potential energy encompasses different types: chemical energy, stored within the bonds of atoms and molecules; mechanical energy, stored within objects through tension or compression; nuclear energy, stored within the nucleus of an atom, maintaining its cohesion; and gravitational energy, stored in an object due to its position in a gravitational field that arises from the gravitational attraction between objects.
On the other hand, kinetic energy includes: radiant energy, which is electromagnetic energy that propagates as transverse waves; thermal energy, also known as heat, arising from the movement of atoms and molecules within a substance; motion energy, stored within objects in motion; sound energy, transmitted through substances in longitudinal waves; and electrical energy, conveyed by tiny charged particles known as electrons.
Despite the diversity of energy forms, a general formula governs energy transfer:
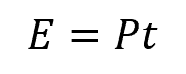
Where:
- E = energy transferred [J]
- P = power or rate of energy transfer [W]
- t = time [s]
According to this equation, the amount of energy transferred is equal to the power consumed or transferred multiplied by the duration or time over which the power is utilized. By multiplying power by time, one can determine the quantity of energy transferred within a given system or process.
Calculating Heat Transfer Using Specific Heat and Latent Heat Capacity
One of the most common examples of energy transfer is the movement of heat.
In thermodynamics, the method of energy calculation depends on the conditions of heat transfer. For a substance undergoing a temperature change without phase change, heat transferred can be calculated using the specific heat capacity, as shown in the equation:
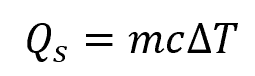
Where:
- Qs = sensible heat transferred without phase change [J]
- m = mass of the substance [kg]
- c = specific heat capacity of the substance [J/kg-K]
- ΔT = change in temperature [K]
Specific heat capacity is a physical property that quantifies the energy needed to increase the temperature of a given mass of a substance. It depends on the substance’s molecular structure and composition. Substances with higher specific heat capacities demand a greater amount of heat energy to elevate their temperature, in contrast to substances with lower specific heat capacities.
If a substance undergoes a phase change, then the heat required for the phase change should be considered in addition to the temperature change. This is called the latent heat of the phase change, which can be calculated using the formula:
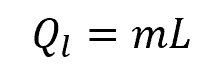
Where:
- Ql = latent heat transferred during phase change [J]
- L = latent heat capacity of the substance [J/kg]
If the substance undergoes multiple phase changes and temperature changes, then the latent heat for each phase change and the sensible heat for each temperature change should be totaled to obtain the overall heat transfer involved in the process.
Calculating Energy Transfer from Charge
When there is a potential difference, such as a voltage applied across a conductor, it creates an electric field. This electric field exerts a force on the charged particles within the conductor, causing them to move.

The transfer of energy occurs due to the work done by the electric field on the charges. This is known as the electric potential energy which is the amount of work required to move a charge from one point to another in an electric field.
This can be calculated using the formula:
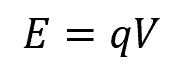
Where:
- q = charge [C]
- V = potential difference [V]
This formula assumes that the charge moves through a constant potential difference, and there are no other factors like resistance or capacitance that may affect the energy transfer.
Calculating Electrical Energy Transfer in a Circuit
Electrical energy transfer in a circuit involves the movement of electrical energy from a power source to a connected load or device. This process includes converting and transmitting electrical energy through circuit components.

In a circuit, a power source, like a battery or generator, generates electrical energy and establishes a voltage difference. This voltage difference creates an electric field that drives the flow of electric charges.
When a circuit is closed, electric charges flow from the negative terminal of the power source through the circuit components back to the positive terminal, creating an electric current. The power consumed by the circuit can be determined by multiplying the voltage across the circuit by the current flowing through it, using the formula:

Where:
- I = electrical current [A]
In electrical systems, measuring the total electrical energy transferred is often done in kilowatt-hours (kWh). To obtain the total kilowatt-hours, use the same general formula equating energy to the product of power and time, but express power in kW and time in hours.
Calculating Electrical Energy Transfer in a Resistor
A resistor is an electrical component designed to have a specific resistance, which restricts the flow of electric current in a circuit according to Ohm’s Law. Ohm’s Law states that the current passing through a resistor is simply the ratio of the voltage and the resistance, as shown in the equation:
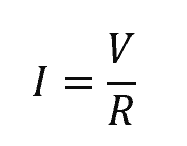
Where:
- R = electrical resistance [Ω]
As the current passes through the resistor, this resistance causes the conversion of electrical energy into heat energy. Using Ohm’s Law, the power dissipated by a resistor can be calculated using the formula:
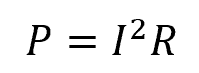
Once the power is calculated, the energy transfer can be obtained using the previously mentioned general formula relating energy, power, and time.
Calculating Motion Energy Transfer due to External Forces
Energy can be transferred from one system to another through the application of external forces. When a force acts on an object and causes it to move, work is done on the object, and energy is transferred.
The energy transferred is equal to the work done and is defined as the product of the applied force and the displacement of the object in the direction of the force. Mathematically, this can be expressed as:

Where:
- W = work done [J]
- F = magnitude of the force applied [N]
- d = displacement of the object [m]
- θ = angle between the force vector and the displacement vector [radians or degrees]
If the force and displacement are both in the same direction, the angle between them is 0 degrees, and the formula simplifies to:
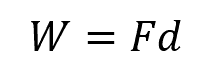
It is important to note that work is a scalar quantity, meaning it only has magnitude and no direction. The direction of energy transfer is determined by the direction of the force and the displacement.

If the force and displacement are in the same direction, positive work is done and energy is transferred to the object. If they are in opposite directions, negative work is done and energy is transferred from the object.
Note that this calculation assumes a constant force and a straight-line path of displacement. If the force or displacement varies, calculating the total work done involves the use of integration.
