In fluid mechanics, total pressure refers to the sum of static pressure and dynamic pressure in a flowing fluid. It represents the energy per unit volume of a fluid and remains constant along a streamline in the absence of external work or heat transfer.

In this article, we will delve into the definition of total pressure, its significance in aerodynamics and hydrodynamics, measurement techniques, and its applications in various engineering fields.
What is Total pressure
In fluid mechanics, total pressure, also known as stagnation pressure, is indicative of the total pressure a fluid would have if it were brought to rest isentropically from its current state of motion. Essentially, it is the sum of the static pressure and the dynamic pressure associated with the fluid’s velocity in a reference frame, as shown in the following equation:
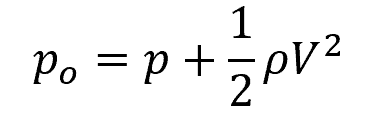

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
Where:
- po = stagnation pressure [Pa]
- p = static pressure [Pa]
- ρ = fluid density [kg/m3]
- V = fluid velocity [m/s]
In the context of aerodynamics, total pressure is encountered at points where the flow speed is zero relative to a body, such as at the leading edge of an airfoil.
Thermodynamically, stagnation properties, including pressure, depend on both the Mach number and the specific heat ratio of a gas. For example, the increase in total pressure across a shock wave can be expressed as a function of the upstream Mach number using compressible flow relations, as shown in the following equation:
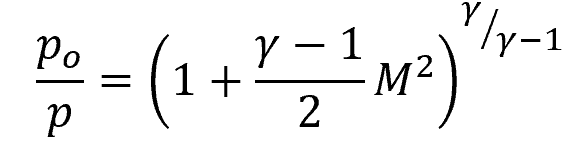
Where:
- γ = adiabatic index [unitless]
- M = Mach number [unitless]
Here, conservation of energy and isentropic assumptions are instrumental in determining fluid properties when the flow is decelerated to a complete stop. These principles are fundamental to the analysis of stagnation conditions and have broad applications in the design of propulsion systems and high-speed aircraft.
Total Pressure in Fluid Mechanics vs Chemistry
In fluid mechanics and chemistry, the concept of total pressure is viewed from distinct perspectives. In fluid mechanics, total pressure refers to stagnation pressure, whereas in chemistry, it is defined as the sum of partial pressures of individual gases, in accordance with Dalton’s Law of Partial Pressures. Mathematically, it can be expressed as:
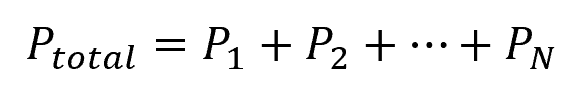
Where:
- P = total pressure of a gas mixture [Pa]
- PN = partial pressure of each gas in the mixture [Pa]
- N = number of gases in the mixture [unitless]
This equation implies that each gas in a mixture behaves independently and contributes to the total pressure as if it were alone occupying the entire volume.
These distinctions between disciplines underscore the comprehensive scope of total pressure within varied scientific contexts. Fluid mechanics views total pressure as a composite measure essential for understanding fluid behavior under different conditions, while chemistry uses total pressure to describe the behavior of gas mixtures.
Measurement Techniques
In the field of fluid dynamics, measuring total pressure is important in the design and analysis of aerodynamic and hydrodynamic components. The measurement techniques for total pressure primarily involve the use of Pitot-static tubes and pressure transducers.
Pitot-Static Tubes
Pitot-static tubes are devices that measure fluid flow velocity and subsequently compute total pressure. They consist of two concentric tubes; the inner tube opens facing the fluid flow and measures the total pressure, while the outer tube has openings along its sides to measure the static pressure, as shown in the diagram below.
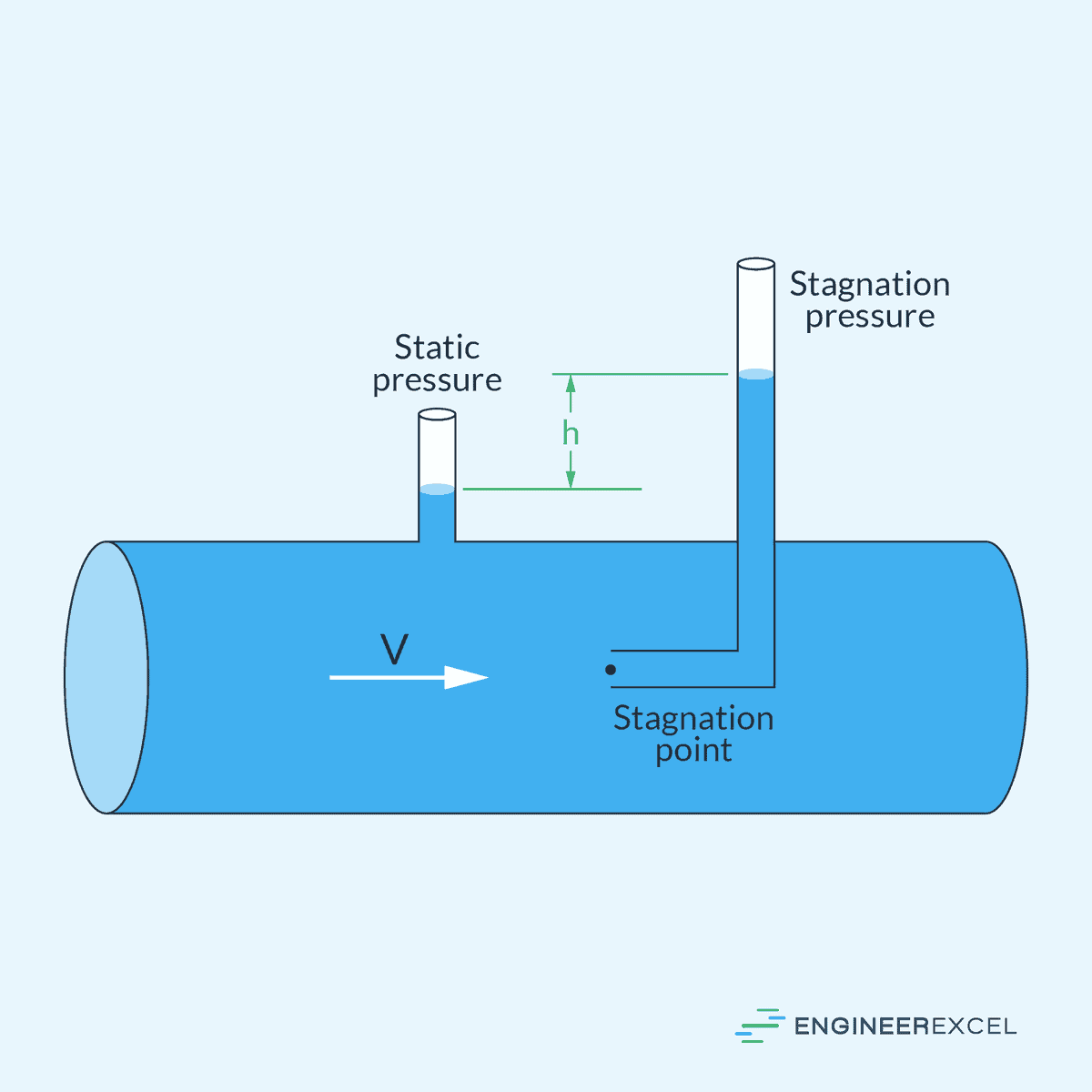
In a supersonic stream, a Pitot tube will have a bow shock ahead of it, which complicates the flow measurement by causing a drop in total pressure.
Pressure Transducers
Pressure transducers, on the other hand, convert pressure into an electrical signal and can be used to measure total pressure directly. These devices typically consist of a diaphragm and a pressure-sensitive element that generates an electrical output proportional to the applied pressure. Such transducers must be accurately calibrated and frequently checked for linearity to ensure precise readings in various fluid environments.
Through a combination of these techniques, engineers can obtain a comprehensive understanding of the flow patterns and characteristics, which is vital for applications ranging from aerospace to mechanical systems that operate within a fluid environment.
Applications in Fluid Dynamics
Total pressure is a critical parameter in fluid dynamics, offering valuable insights into fluid flow behavior over objects. By assessing total pressure, engineers can predict flow patterns and determine the aerodynamic or hydrodynamic forces acting on bodies.
Aerodynamics
In aerodynamics, total pressure plays a vital role in the analysis of air flow around aircraft. Engineers use the concept of total pressure to calculate the lift and drag forces, which are essential for aircraft design and performance optimization.
For example, the total pressure ratio across a shock wave is essential for understanding supersonic flight characteristics. These calculations often involve the use of the total pressure jump relation for compressible flow, which is a function of the upstream Mach number.
Hydrodynamics
In hydrodynamics, total pressure is essential for analyzing the flow around submerged objects like ship hulls, submarines, or offshore structures. This pressure is used to evaluate the fluid loads on structures and their responses to such loads. For example, the impact of total pressure can be evaluated to design hulls that minimize resistance in water, thus improving the efficiency of vessels.
It is also important to note that high total pressures can lead to cavitation around propellers and other underwater components. Understanding the total pressure helps in designing to avoid such undesirable effects.
Sample Problem
Problem: A pitot tube is used to measure the flow of water in a pipe. The total pressure measured by the pitot tube is 100 kPa, and the static pressure is 60 kPa. Determine the velocity of the water flow in the pipe.
Solution:
The total pressure is given by the formula:
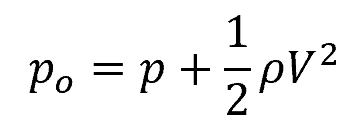
Rearranging the above equation to obtain the velocity:
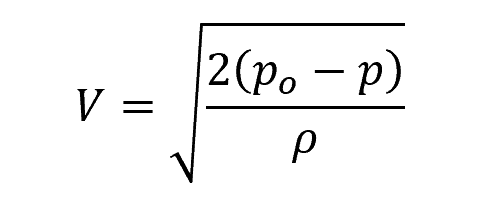
Given po = 100 kPa, p = 60 kPa, and ρ = 1000 kg/m3, we can solve for V as follows:

Therefore, the velocity of the water flow in the pipe is 8.94 m/s.
