Poisson’s ratio is a measure of the relative change in dimensions perpendicular to the direction of an applied force, typically in a material undergoing deformation. It quantifies how much a material will contract or elongate in the perpendicular direction when stretched or expanded in another direction.

In this article, we will explore the concept of Poisson’s ratio, its calculation, relation to elastic moduli, factors affecting its value, and its significance in understanding the deformation characteristics of different materials.
Poisson’s Ratio Explained
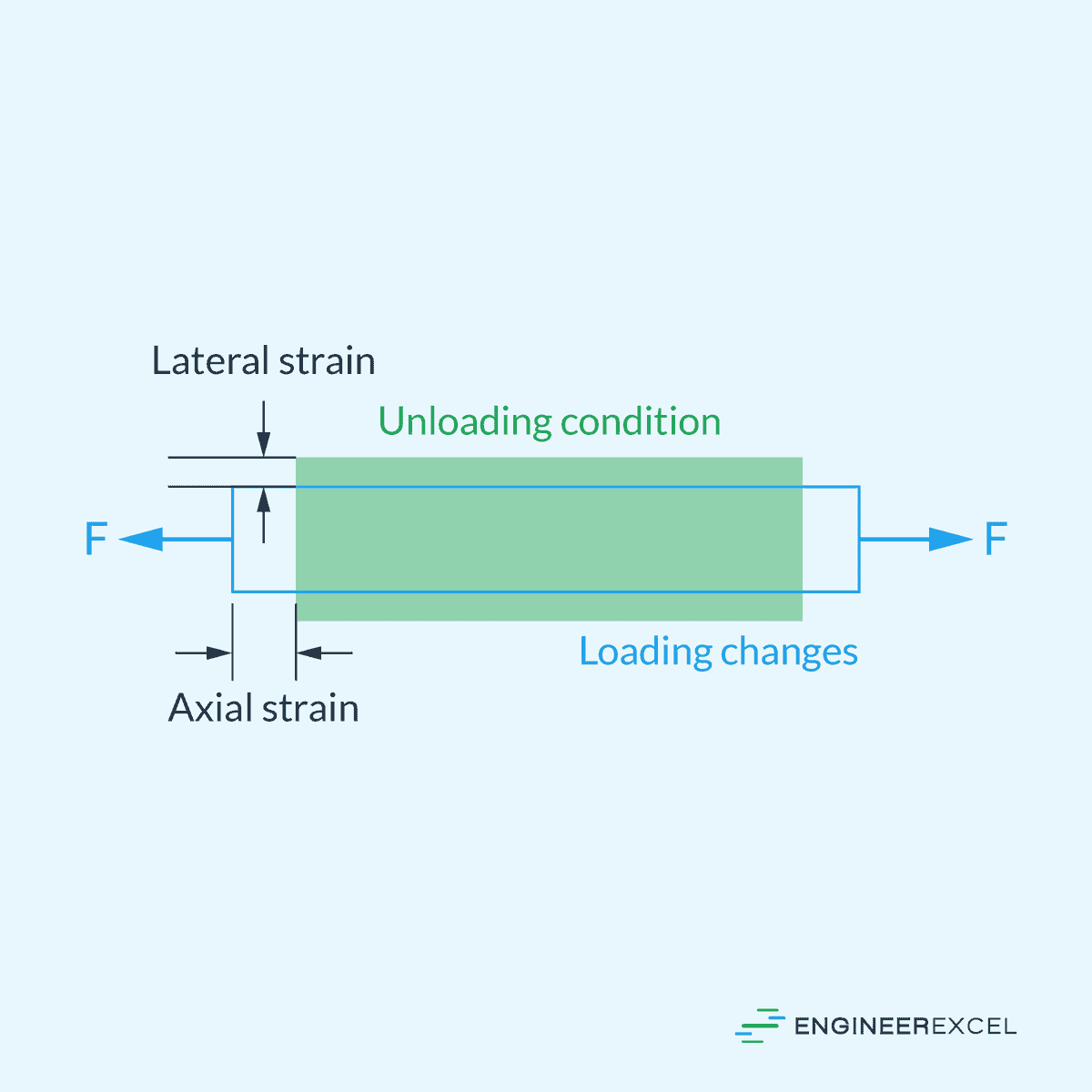
The design of structures often involves studying how materials deform under different loads. A key concept in material deformation is understanding the relationship between longitudinal strain and lateral strain.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
When materials are stretched or compressed, they tend to contract or expand in directions perpendicular to the applied load. This means that aside from the longitudinal strain experienced by the material along the direction of the load, the material also experiences lateral strain in the transverse direction of the load.
This behavior can be quantified using a parameter called Poisson’s ratio. Named after Simeon Poisson, a French mathematician who made significant contributions to the theory of elasticity, Poisson’s ratio is a dimensionless constant defined as the negative ratio of the lateral strain to the longitudinal strain in the direction of the applied force.
This is expressed mathematically as:

Where:
- ν = Poisson’s ratio [unitless]
- εlat = lateral strain [unitless]
- εlong = longitudinal strain [unitless]
Typically, the value of Poisson’s ratio ranges from 0 to 0.5 for most materials. Rubber-like materials may have a ratio near 0.5, indicating significant lateral expansion. In contrast, materials with a ratio close to 0 show negligible lateral deformation.
Auxetic Materials
It is important to note that there are some materials, like re-entrant foam, with negative Poisson’s ratio. These materials exhibit the counterintuitive characteristic of becoming wider in cross-section when stretched and narrower when compressed, which is the opposite behavior to that of most materials. This unusual property is termed “auxetic,” and it arises from the specific internal structure of these materials.
For example, re-entrant foam is designed with a repeating pattern of structures, often with a bow-tie or star-like shape, that allows the material to expand laterally when pulled. The unique geometric arrangement of the solid parts of the foam causes them to rotate and create a denser structure when under tension, leading to the auxetic behavior.
The negative Poisson’s ratio has practical applications, including high energy absorption, which makes it useful for protective gear, and the ability to create custom-fit products through its conformability. Additionally, because auxetic materials can potentially exhibit enhanced mechanical properties such as shear stiffness and resistance to fracture, they are useful for various applications including medical devices, aerospace, and flexible electronics.
Relation to Elastic Moduli
Poisson’s ratio can be related to the elastic moduli of a material (such as Young’s modulus, shear modulus, and bulk modulus) using a set of equations that are derived from the general equations of elasticity for isotropic, linearly elastic materials. These are mathematically expressed as follows:
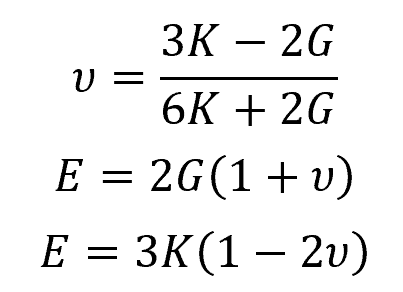
Where:
- E = Young’s modulus [Pa]
- G = shear modulus [Pa]
- K = bulk modulus [Pa]
These relationships show that if you know any two of Young’s modulus, shear modulus, bulk modulus, and Poisson’s ratio, you can calculate the third elastic modulus. It’s important to note that these equations assume the material behaves in a linear and isotropic manner, which means its properties are the same in all directions and the stress-strain relationship is linear. Materials that do not meet these criteria may not adhere strictly to these relationships.
Factors Affecting Poisson’s Ratio
Poisson’s Ratio is influenced by a number of factors inherent to materials, including their composition, structural anisotropy, and temperature. These factors must be considered when predicting the behavior of materials under stress.
Material Composition
Different materials have unique interatomic bonding and structural arrangements, leading to variations in their ability to deform laterally when stretched or compressed. For instance, brittle materials like ceramics typically have a lower Poisson’s Ratio because their rigid atomic structures resist lateral deformation. Conversely, ductile materials such as metals can have a higher Poisson’s Ratio as their more flexible atomic lattices allow for greater transverse strain.
Polymers exhibit a wide range of Poisson’s Ratios due to their complex molecular structures, which can be tailored by modifying their composition, such as by adding plasticizers. Composite materials, which combine two or more distinct phases, can have engineered Poisson’s Ratios by adjusting the volume fraction and properties of the constituent materials.
Material Anisotropy
Material anisotropy refers to the directional dependence of a material’s properties. In isotropic materials, properties like Young’s modulus and Poisson’s Ratio are consistent in all directions. However, in anisotropic materials, such as composites or crystalline solids with non-cubic symmetry, these properties vary with direction, resulting in different Poisson’s Ratios along different axes.
For example, in a unidirectionally reinforced composite, the Poisson’s Ratio may be higher in the direction perpendicular to the fibers compared to the longitudinal direction. This anisotropy can be exploited in engineering to create materials with tailored mechanical responses under stress.
Temperature
Generally, as temperature increases, materials tend to become more ductile, which can result in an increase in Poisson’s Ratio, as observed in some studies where Poisson’s Ratio approaches 0.5 near the glass transition temperature for polymers. However, the effect of temperature on Poisson’s Ratio is not universal and can vary depending on the material’s composition and structure. For instance, in some materials, Poisson’s Ratio may actually decrease with an increase in temperature due to relaxation of the material’s structure.
The relationship between temperature and Poisson’s Ratio is also influenced by the phase of the material; for example, a polymer may exhibit different Poisson’s Ratios in its glassy, rubbery, or melt phases. It is important to note that the temperature effect is generally small, but it must be considered in precision applications where thermal variations could affect mechanical performance.
Poisson’s Ratio of Different Materials
Materials respond to stress in various ways, and the Poisson’s ratio is a critical factor in understanding their deformation characteristics. The value of Poisson’s ratio varies among different materials, influencing how they are utilized in engineering applications.
The table below lists the typical values of Poisson’s ratio for some common engineering materials.
