In structural engineering, statically determinate structures refer to those that can be analyzed using equilibrium equations alone. On the other hand, statically indeterminate structures require extra conditions or properties to solve for unknown reactions.

In this article, we will cover the difference between statically determinate and indeterminate structures, the statical determinacy of trusses and planar frame structures, and the benefits of indeterminacy in structural engineering.
What Are Statically Determinate and Indeterminate Structures
Analyzing forces and moments within a structure is important for understanding its performance under various load conditions. To do this, engineers typically use equilibrium equations that describe the balance of forces and/or moments acting on the structure. The complexity of these calculations depends on the object’s geometry and the number of unknowns.
For example, for a one-dimensional body, such as a beam or truss member, there are 2 independent equilibrium equations: one for the sum of forces in the axial direction (usually horizontal) and one for the sum of moments about any point.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
In a two-dimensional body, like a plane or frame structure, there are 3 independent equilibrium equations: one for the sum of forces in the horizontal direction, one for the sum of forces in the vertical direction, and one for the sum of moments about any point.
For a three-dimensional body, such as a space truss or frame, there are 6 independent equilibrium equations: three for the sum of forces along each of the three orthogonal axes (x, y, and z directions) and three for the sum of moments about each of the three axes.
Based on the relationship between the number of unknown forces and moments and the number of independent equilibrium equations, engineers classify structures into two categories: statically determinate and statically indeterminate structures.
A statically determinate structure is one where the number of unknown forces and moments is exactly equal to the number of independent equilibrium equations that can be written for the structure. In such cases, all unknowns can be found using only the equilibrium equations without the need for additional information or analysis. For example, in a simple beam or truss, if there are as many unknowns as there are equilibrium equations, the structure is statically determinate.
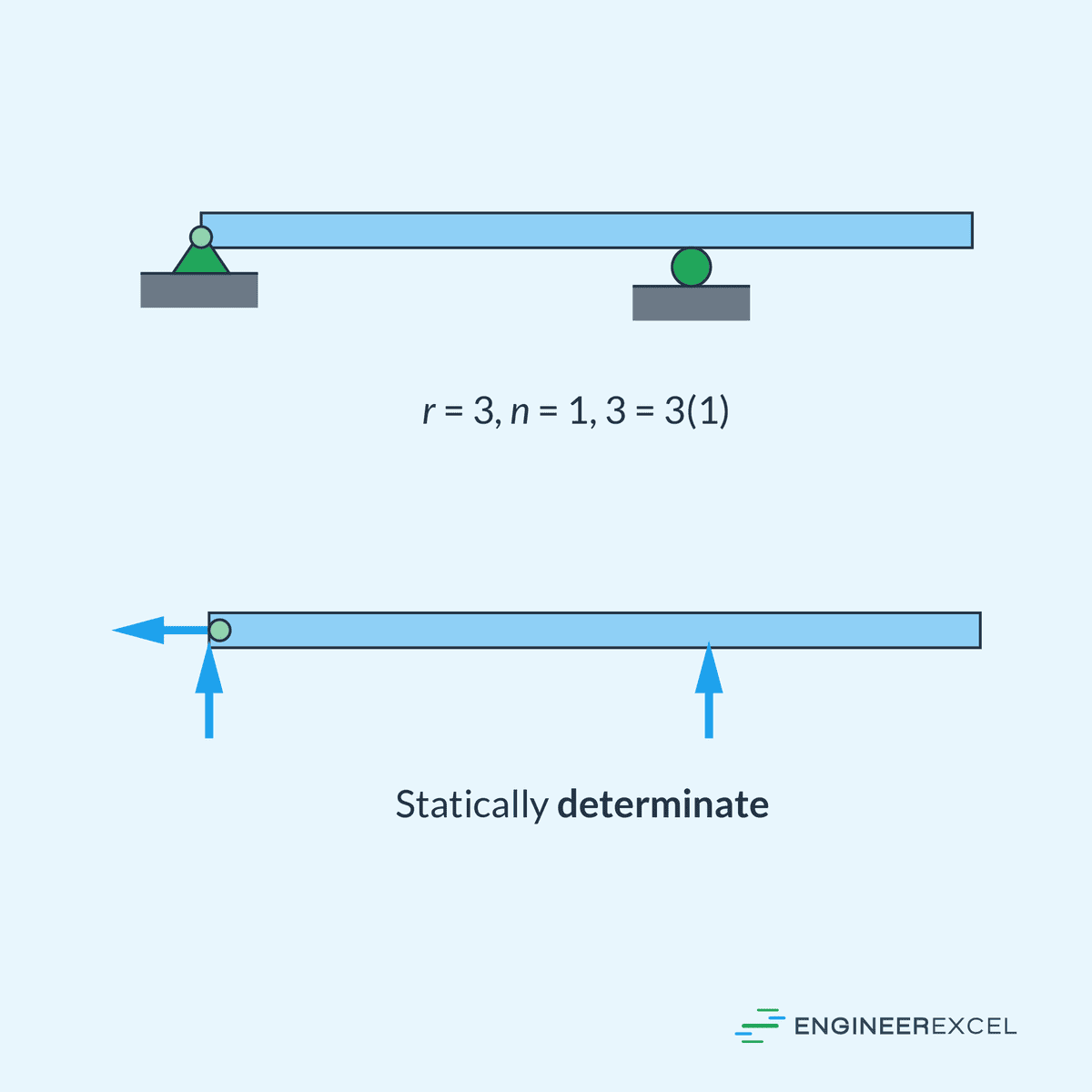
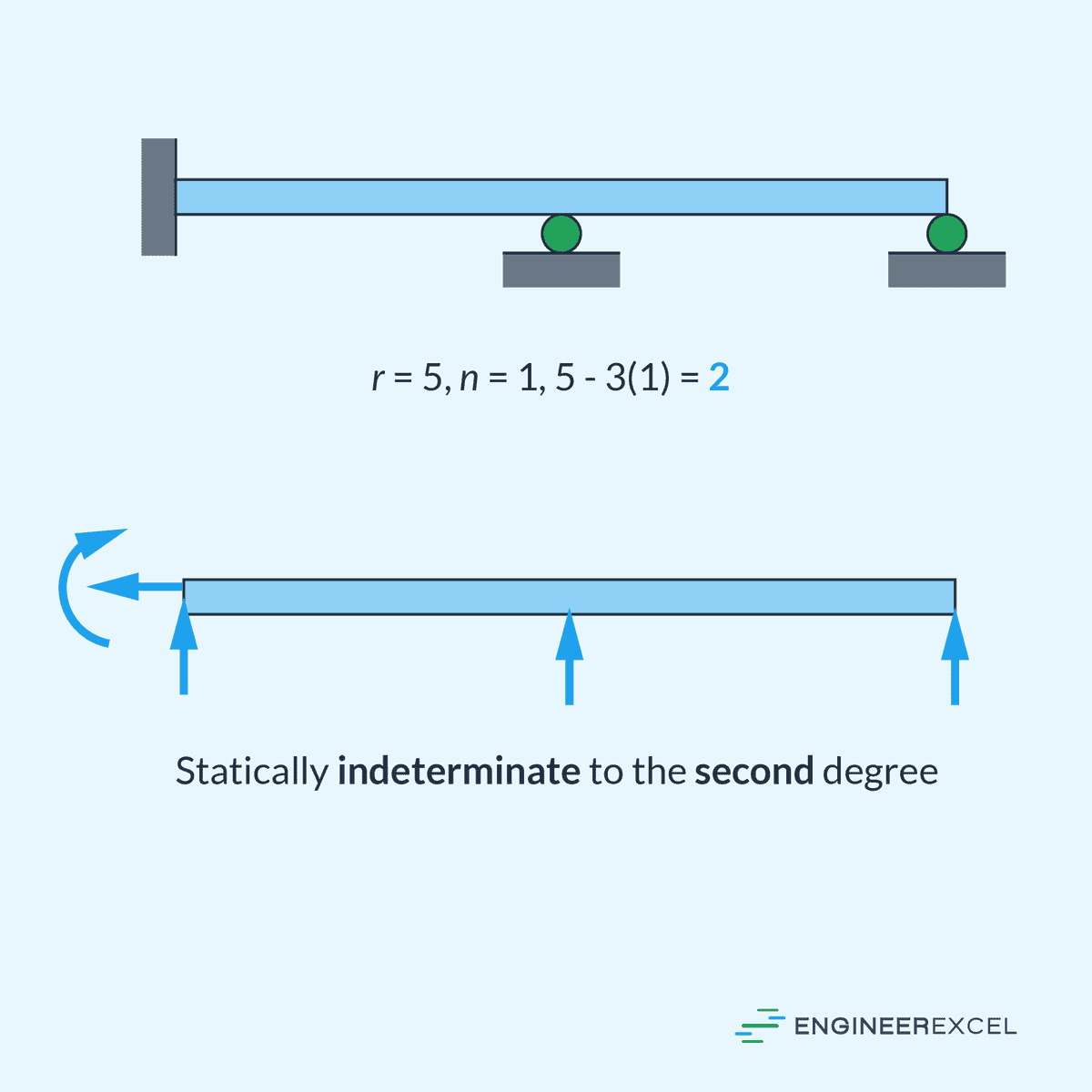
On the other hand, a statically indeterminate (or hyperstatic) structure has more unknown forces and moments than there are independent equilibrium equations. In such cases, the equations of equilibrium alone are insufficient to solve for all unknowns. Additional methods, such as compatibility equations based on deformations, must be used to solve for the extra unknowns.
Statically indeterminate structures have extra supports or members, known as redundant, which are not necessary for maintaining equilibrium. These result in additional internal forces and moments that cannot be determined by statics alone. Hence, they require a more complex analysis, often involving the material properties and the geometry of the structure.
Examples include continuous beams, which are beams spanning across more than two supports, and architectural frames with multiple members joined rigidly, creating an intricate network.
Statical Determinacy of Trusses
To determine the statical determinacy of trusses, we use the relative magnitude between the number of joints, members, and unknown reaction forces. If the structure is statically determinate, the following condition should apply:
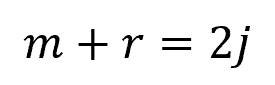
Where:
- m = number of members [unitless]
- r = number of unknown reaction forces [unitless]
- m = number of joints [unitless]
Otherwise, if the structure is statically indeterminate:
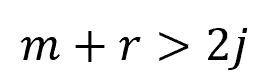
Note that, in order for a truss to be useful for practical applications, it must be stable. Stability means that it retains its shape and does not collapse under load. For example, if member reactions are concurrent or some of the components form a collapsible mechanism, then the structure is unstable.
Furthermore, a truss is generally considered unstable if:

Statical Determinacy of Planar Frame Structures
In planar frame structures, each free body diagram has three equations of equilibrium. Therefore, to determine statical determinacy, we compare the number of unknown reaction forces to thrice the number of members. Thus, if the structure is statically determinate, the following condition should apply:
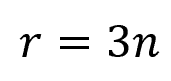
Where:
- n = number of members [unitless]
Otherwise, if the structure is statically indeterminate:
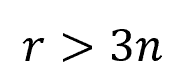
A planar frame structure is generally considered unstable if:
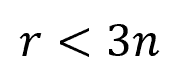
Degree of Static Indeterminacy
The Degree of Static Indeterminacy (DSI) of a structure refers to the number of additional equations required to solve for the internal forces and reactions beyond the basic equilibrium equations. For a beam or frame, it is calculated by subtracting the number of available equilibrium equations from the total number of unknown forces.
In a planar structure, there are three equilibrium equations available, and for spatial structures, there are six. If the DSI is zero, the structure is statically determinate; if it is positive, the structure is statically indeterminate. The higher the DSI, the more complex the analysis becomes, as it requires additional compatibility conditions to solve for the unknowns.
Advantages of Indeterminacy
Initially, engineers may prefer to design statically determinate structures because they are simpler to analyze; the internal forces and moments can be determined solely from the equations of equilibrium without considering material properties or deformation. However, in structural engineering, indeterminate structures offer several advantages compared to their determinate counterparts.
Foremost among these is the redundancy they provide. Indeterminate structures typically have multiple load paths, which means failure in one element does not lead to immediate collapse. This characteristic enhances reliability and safety.
Another advantage is the distribution of loads amongst various members of the structure. It allows for more efficient material usage, as stresses are shared and not concentrated on a singular path. This can lead to cost savings in both material expenses and long-term maintenance.
From a dynamic response perspective, indeterminate structures often exhibit reduced vibrations. These structures inherently dampen vibrations better due to extra members and connections, providing improved comfort for occupants and stability for sensitive equipment.
Indeterminate structures also afford greater flexibility in design. They can be engineered to meet complex architectural requirements, enabling novel forms and larger spans without intermediate supports. This flexibility can prove vital in urban environments where space is at a premium.
Lastly, the use of modern computational tools has greatly simplified the analysis of indeterminate structures, making them more accessible and feasible for a wide range of projects. With sophisticated software, the once daunting task of calculating internal forces and moments in these structures is now streamlined.
