Elastic deformation is a reversible change in the shape or size of a material in response to an applied force, where the material returns to its original shape once the force is removed. It occurs within the material’s elastic limit, where the atomic or molecular structure can temporarily distort without permanent damage. In this article, we will delve into the mechanics of elastic deformation, its different modes, stress-strain relationships, and practical applications in various engineering fields.
Understanding Elastic Deformation
Elastic deformation is a type of material strain where a solid body temporarily changes shape when stress is applied. Upon removal of the stress, the material returns to its original shape. This type of deformation occurs at low stress levels, within the elastic limit of the material, which is the maximum extent to which the material can be deformed without causing permanent deformation.
The behavior of materials undergoing elastic deformation can be explained by their atomic and molecular structure. Atoms and molecules form a lattice structure within the solid and are bonded together by interatomic forces.
When stress is applied, these bonds are stretched but do not break; instead, they act like tiny springs, storing the energy from the stress. The material’s ability to withstand elastic deformation depends on the strength and stiffness of these bonds, which determine the force required to deform the material.
Elastic deformation is a critical concept in many engineering applications because it determines how materials will respond to forces. Engineers must ensure that the stresses and strains within materials remain within the elastic range to avoid permanent deformation or failure. For example, when designing bridges, buildings, or airplane wings, the structures must be able to bend slightly under load but return to their original shape to maintain integrity and safety.
Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
However, if the stress exceeds the material’s elastic limit, it enters the plastic deformation phase, where the deformation becomes permanent, and the material does not return to its original shape after the load is removed. This transition from elastic to plastic behavior marks the yield point of the material, which is a critical design threshold.
Understanding the difference between elastic and plastic deformation is essential for material selection and engineering design to ensure that components can withstand the loads they will encounter during their service life without experiencing failure.
Types of Elastic Deformation
Elastic deformation can be categorized into three primary modes based on the nature of the applied stress: axial (tensile or compressive), shear, and bulk.
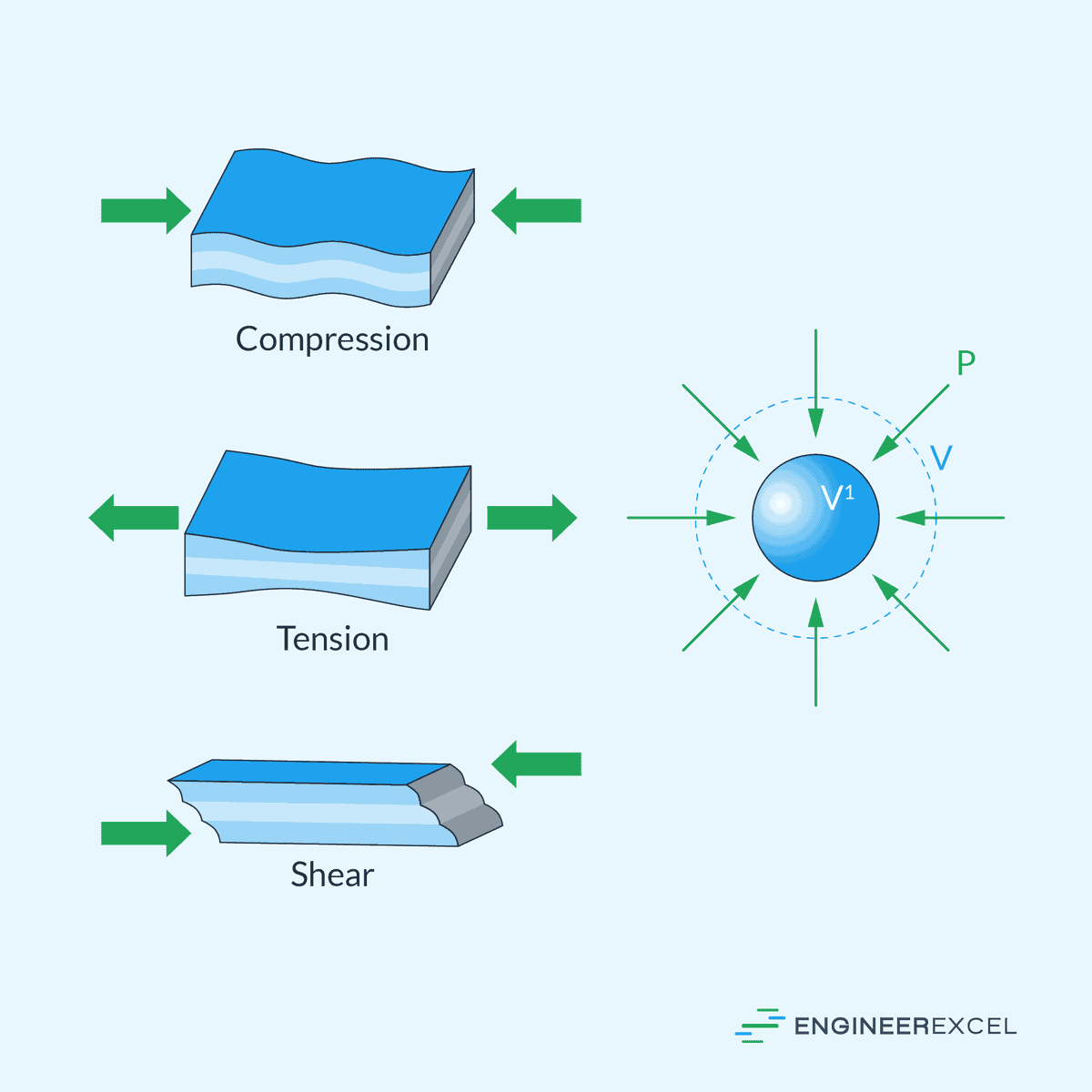
Axial Deformation
Tensile Deformation
When a material experiences a pulling or stretching force, it undergoes tensile deformation. This is characterized by an elongation of the material along the direction of the applied force. The extent of tensile deformation a material can withstand is a measure of its tensile strain, which is a dimensionless ratio of the change in length to the original length.
Compressive Deformation
Compressive deformation occurs when a material is subjected to squeezing or pushing forces. The stress results in a shortening of the material in the direction of the applied pressure. During compression, materials exhibit compressive strain, calculated similarly to tensile strain as the ratio of change in length to the original length but with values indicating reduction rather than elongation.
Shear Deformation
Materials exposed to forces acting parallel to each other but in opposite directions experience shear deformation. It is observed as a distortion or slippage along the plane subjected to the shear stress, resulting in a change of shape without a change in volume. The degree of shear deformation is measured by the shear strain, quantified as the displacement of one layer relative to another divided by the initial separation of the layers.
Bulk Deformation
Bulk deformation refers to the change in volume of a material in response to an applied stress, typically resulting in compression or expansion of the material uniformly in all directions. This type of deformation occurs when the material experiences stress that is distributed evenly throughout its volume, leading to a change in its overall shape without significant distortion or localized deformation. It is commonly observed in materials like rubber or fluids under hydrostatic pressure, where the applied stress causes the material to compress or expand uniformly.
Stress and Strain Relationship
Understanding the relationship between stress and strain is important in analyzing elastic deformation. Stress refers to the internal forces that particles of a material exert on each other, typically measured in units of pressure such as pascals (Pa). Strain indicates the deformation of the material in response to stress, defined as the change in dimension over the original dimension, and is dimensionless.
For axial deformation, Hooke’s Law describes the stress-strain relationship, stating that within the elastic limit of a material, the applied stress is directly proportional to the resulting strain:
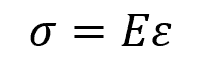
Where:
- σ = axial stress [Pa]
- E = Young’s modulus [Pa]
- ε = axial strain [unitless]
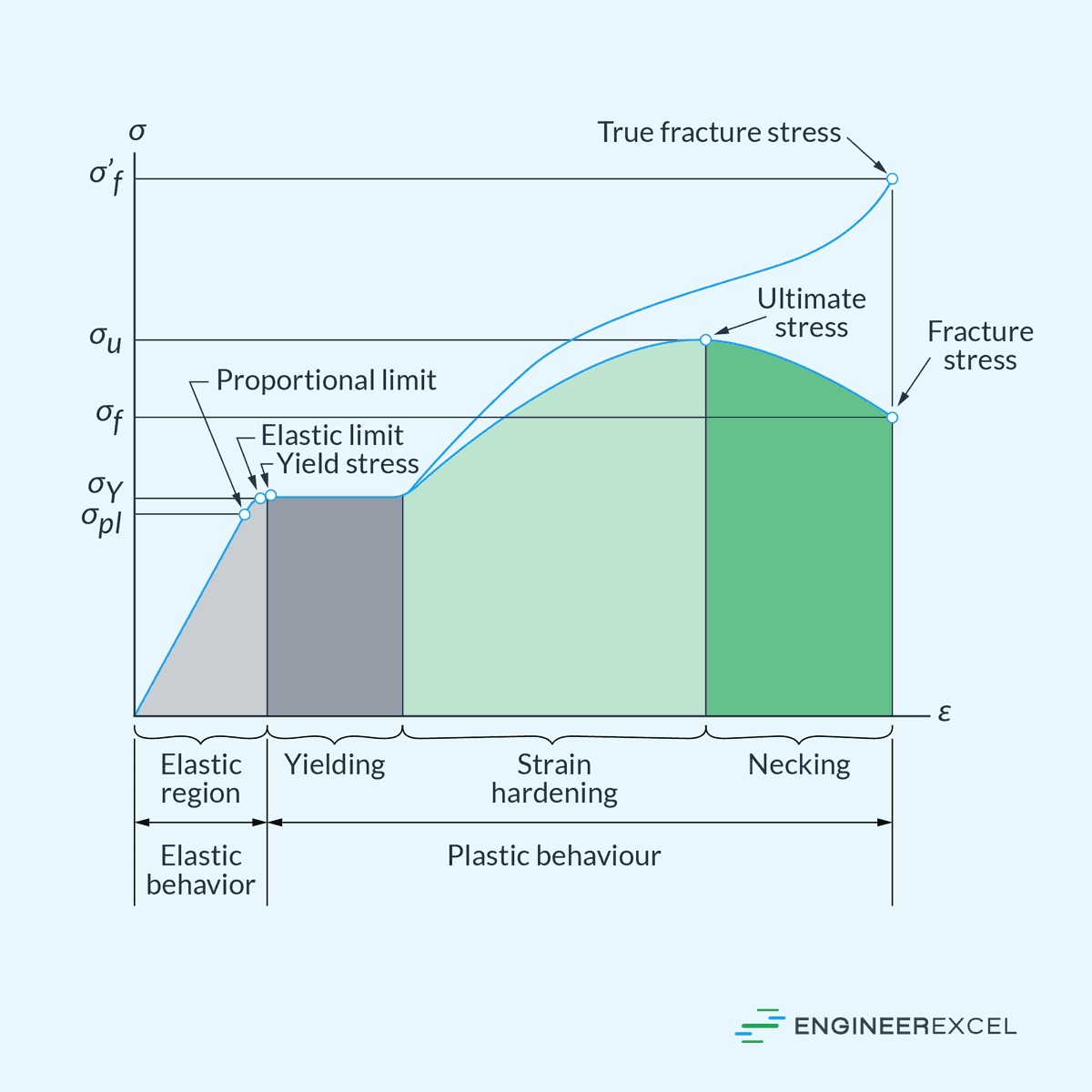
Materials subjected to stress display a linear relationship up to a certain limit, known as the proportional limit, beyond which permanent deformation occurs. The region within this limit is known as the elastic region, as shown in the diagram below.
Similarly, for shear deformation, the stress-strain relationship is described by the formula:
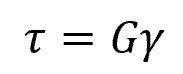
Where:
- τ = shear stress [Pa]
- G = shear modulus [Pa]
- γ = shear strain [unitless]
Lastly, for bulk deformation, the stress-strain relationship is described by the formula:
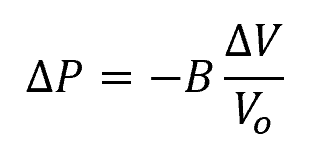
Where:
- ΔP = bulk stress [Pa]
- B = bulk modulus [Pa]
- ΔV = change in volume [m3]
- Vo = original volume [m3]
The negative sign indicates an increase in pressure causes a decrease in volume.
Young’s modulus, shear modulus, and bulk modulus are all measures of a material’s response to different types of elastic deformation. Young’s modulus describes how a material deforms under tensile or compressive forces, shear modulus quantifies its response to shearing forces, and bulk modulus measures its resistance to uniform compression.
Applications of Elastic Deformation
Structural Analysis
In structural analysis, engineers use elastic deformation principles to predict how buildings, bridges, and other structures will respond to loads. This includes calculating expected displacements and rotations of structural elements to ensure safety and stability under normal and extreme conditions. Analyzing the elastic properties of materials allows for designing structures that can withstand anticipated stresses without permanent deformation.
Machining Tolerances
Precise control of elastic deformation is important in machining processes to maintain tolerances. During the application of cutting forces, components experience elastic deformation, which must be appropriately compensated for in the design stage to achieve the desired dimensions and geometries after the removal of the applied forces.
Springs and Cushioning Devices
The design of spring and cushioning devices, from simple coil springs to complex energy-absorbing architectures, depends heavily on the elastic properties of the materials to store and release energy as needed for applications such as vehicle suspension systems and vibration dampeners.
