Lateral strain refers to the deformation experienced by a material perpendicular to the direction of applied force or stress. It is typically measured as a ratio of lateral displacement to the original lateral dimension.

In this article, we will delve into the concept of lateral strain, its calculation, and measurement methods.
Understanding Lateral Strain
In engineering, strain represents the deformation of materials under applied stress. It is a dimensionless measure of deformation, typically expressed as a change in size relative to original dimensions.
Depending on the orientation of the applied stress, strain may be experienced in different directions. In general, when a material is stretched or compressed along one axis, it often contracts or expands along the other two axes. This type of strain that occurs perpendicular to the applied stress is called lateral strain.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
To illustrate, consider the diagram of a bar under tensile load below.

As the horizontal bar is pulled in tension, it experiences elongation in the horizontal direction due to the applied force. This means that the length of the bar increases along the direction of the force.
However, the bar also experiences lateral contraction, meaning it becomes narrower in the transverse direction perpendicular to the applied force. This lateral contraction occurs as the material redistributes internally, as a result of the conservation of material volume.
The behavior of lateral strain varies depending on the material’s properties. For example, in rigid materials such as enamel, the lateral strain is usually small because these materials do not easily change shape in response to stress. Conversely, ductile materials, like metals, can exhibit more significant lateral strain as they are more malleable and can deform more before fracturing.
Calculating Lateral Strain
To calculate lateral strain during a uniaxial stress test, one must measure the original width of the specimen and its width after force application. The difference between these two widths, when divided by the initial width, provides the lateral strain value.
This is mathematically expressed as:
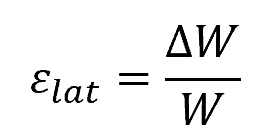
Where:
- εlat = lateral strain [unitless]
- ΔW = change in width of the material [m]
- W = original width of the material [m]
An important factor in these calculations is Poisson’s ratio, a fundamental material property that relates lateral strain to the longitudinal strain. This ratio is important because it allows for the determination of lateral strain based on longitudinal strain data, simplifying the calculation process when longitudinal strain is known.
Poisson’s Ratio is unitless and is typically derived from the equation:
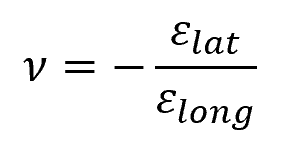
Where:
- ν = Poisson’s ratio [unitless]
- εlong = longitudinal strain [unitless]
Poisson’s ratio varies between materials and is often obtained from technical datasheets or through specific laboratory testing.
The negative sign in the equation above signifies that a positive longitudinal strain typically results in a negative lateral strain. This means that when a material elongates along the axial direction, it usually contracts in the transverse direction. However, it is important to note that, while this is a general principle, there are exceptions in some materials that do not conform to this behavior.
These materials are known as auxetic materials. Auxetic materials exhibit the unusual behavior of expanding in the transverse direction when subjected to a tensile load, contrary to the typical behavior described by Poisson’s ratio.
Measurement of Lateral Strain
Measuring lateral strain is important because it provides insight into the material’s deformation characteristics under stress. There are various methods to do this, including the use of strain gauges and optical methods.
Strain Gauges
By sticking a strain gauge to a material, minute deformations can be detected due to changes in the gauge’s electrical resistance. For lateral strain measurements, it is essential to position the gauge perpendicular to the applied load. This configuration allows the gauge to capture the transverse deformation.
Optical Methods
Optical methods offer non-contact means of measuring strain, with digital image correlation (DIC) being a prominent technique. DIC employs pattern recognition between images of the undeformed and deformed states of the material, enabling a full-field measurement of strain.
The method’s sensitivity allows for the detection of strain without physically contacting the material, thus avoiding any additional stress or strain that may affect the measurement. Optical methods are particularly useful when dealing with delicate or very small samples where traditional tactile sensors might influence the material’s properties.
Example Problem
Problem: A 1-m steel rod with a width of 50 mm is subjected to a tensile stress that causes it to elongate by 1 mm. The Poisson’s ratio for steel is typically around 0.3. Calculate the lateral strain experienced by the rod and its final width.
Solution:
We are given: ν = 0.3, ΔL = 1 mm, L=1 m, and W=10mm
We need to calculate the lateral strain, but first, we need to determine the longitudinal strain, which is the change in length divided by the original length:
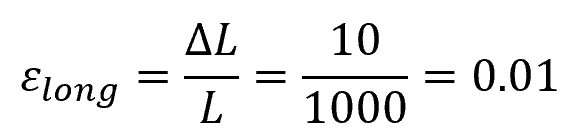
Now, we can use Poisson’s ratio to find the lateral strain:

The negative sign indicates that the lateral strain is in the opposite direction to the longitudinal strain, which means the rod gets thinner as it gets longer. To find the actual change in width, we can apply the lateral strain to the original diameter:
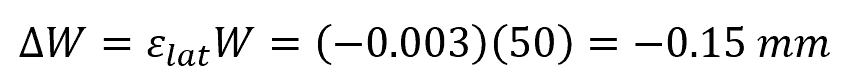
Calculating for the final width:
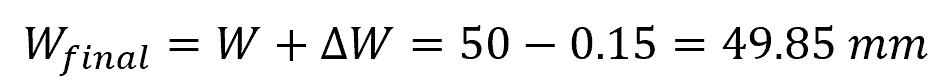
Therefore, the lateral strain experienced by the rod is -0.003 and its final width is 49.85 mm.
