Parallel Heat Exchangers Explained

The purpose of a heat exchanger is to transfer heat energy from one fluid to another, with the two fluids existing initially at different energies and temperatures. What it means to be a parallel is that the two fluids enter and leave from the heat exhanger in the same directions. Heat exchangers are widely used across the world, from homes to giant industrial buildings, and as we will see parallel exchangers are not the only type, but are best for certain situations.

How Does a Parallel Heat Exchanger Work?

Heat exchangers do exactly that: they purposefully exchange heat, and the heat energies, between two fluids. They are widely used in both heating and cooling applications. An everyday example of a heat exchanger is the combustion engine of a car, where cooling fluid passes through inside the coils of a radiator as outside air moves around the radiator. The air flowing around takes heat energy from the coolant fluid, in the process heating up and cooling the fluid.

A parallel heat exchanger is a specific type of exchanger in which the two fluids are moving in the same direction, in parallel, through the exchanger. The two fluids can either be separated by solid walls or tubes to prevent them from mixing, or can be in direct contact with each other. Which design is used is entirely dependent on the situation.

In its most basic form, a heat exchanger consists of tubes with one type of fluid moving through them, and a second fluid flowing around the outside of the tubes. The other main type of heat exchanger is called a counter-flow heat exchanger, in which the two fluids move in opposing directions.

Elevate Your Engineering With Excel

Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.

Find Out More

Heat exchangers have three different modes in which heat energy is transferred when they are made up of tubes and open channels. They are:

1. Convective heat transfer from the contained fluid to the inner wall of the tube
2. Conductive heat transfer through the tube wall, from inner to outer surface
3. Convective heat transfer from the outer tube wall to the open channel fluid

where these three forms can be reversed if the fluid outside the tubes is hotter than the fluid contained in them.

Where Are Parallel Heat Exchangers Used?

Parallel heat exchangers are less common than their counter-flow cousins, but still see some use in certain applications. While less efficient, the main advantage of parallel heat exchangers is that the exit temperature of the two fluids, and therefore their energies, will be closer to one another than they would be in counter-flow exchangers.

Why might this be better? When the two fluids are closer together in final temperature, it also means that the two sides of the tube walls separating them are closer together in temperature. And in a lot of materials this means less and slower corrosion, which is important for maintaining the life of the heat exchangers.

Parallel flow heat exchangers are also good if you want to keep the maximum temperature of the colder fluid below a certain threshold. While less efficient, sometimes its important not to transfer too much heat, which is where a parallel exchanger would be handy.

Also, while parallel exchangers will not transfer as much heat as with a counter-flow device, if the temperature difference between the two fluids is large enough, parallel exchangers will bring the fluids closer to equilibrium faster. Finally, sometimes its impossible to prevent parallel flow in certain exchangers, leaving this as the only option.

So what are some examples of parallel heat exchangers? For one, many furnaces operate as parallel exchangers to prevent some of the corrosion of the metal with large temperature differences.

Another common example is in gas or petroleum processing, where keeping gases below or above a certain temperature is very important. By restricting the final temperatures, these power plants prevent gases from changing their chemical states and potentially freezing, compressing, or forming as liquids.

Which is Better: Parallel or Counter Flow?

As discussed above, there are appropriate applications for both parallel and counter flow heat exchangers. However, on the whole, counter flow heat exchangers are more effective, and therefore used more frequently.

This is because the outlet temperature of the cold fluid in a parallel exchanger with always be less than the outlet temperature of the hot fluid you are trying to cool. In counter flow heat exchangers, this restriction does not exist, and you are able to actually cool the hot fluid to a level below the “cold” fluid at the outlet.

The differences between the rates of heat transfer between the two exchangers naturally derives from the direction fluids flow within them, and has to do with the difference in temperature gradients with the exchangers. Take the example of a hot fluid moving through the tubes, and the cooling fluid moving in the open outside the tubes.

In a counter flow exchanger, as the hot fluid moves along the tube, it will be “met” by increasingly colder fluid outside the tubes moving in the opposite direction, helping to maintain a strong cooling process with a large temperature difference between the fluids for the entire length of the exchanger. This process is the same (but in reverse order) for the cold fluid heating up at a relatively higher rate.

If this example took place in a parallel heat exchanger, the two fluids would enter in at their coldest and hottest points, respectively. But as the two fluids move in sync across the exchanger, they are moving closer to equilibrium and therefore getting heated/cooled at a lower rate, because there is less of an energy difference between the two fluids. So, while a parallel heat exchanger has plenty of uses as discussed above, we can see why it is less efficient and less common for heating/cooling applications.

Parallel Flow Heat Exchanger Formula

There are a number of equations used to find things like the efficiency and rate of heat transfer in various heat exchangers. Here we will look at a few used for parallel exchangers:

Efficiency is defined as the rate of actual heat transfer to the ideal rate:

where:

• η = efficiency of heat exchange (unitless)
• q_act = rate of actual heat transfer (W/m²)
• q_ideal = idealized, unreal rate of heat transfer (W/m²)

The actual rate of heat transfer can be found by looking at either one of the fluids in the exchanger like so:

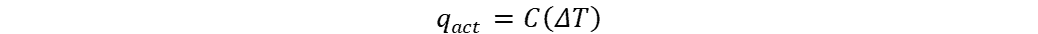
where:

• C = heat capacity of a fluid (J/K)
• ΔT = change in temperature of fluid between start and end (degrees Kelvin)

The ideal rate of heat transfer is found as so:

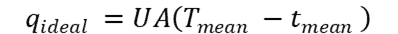
where:

• U = overall average heat transfer coefficient (W/m²*℃)
• A = surface area over which transfer occurs (m²)
• T_mean = mean temperature of hot fluid across exchanger ( degrees Kelvin/Celsius)
• t_mean = mean temperature of cold fluid across exchanger (degrees Kelvin/Celsius)

To calculate this difference in mean temperatures we can use the following simple formula:

where:

• T_{1, 2} = start and end temperature of hot fluid (degrees Kelvin)
• t_{1, 2} = start and end temperature of cold fluid (degrees Kelvin)