Steel is one of the most widely used materials in the world and its thermal properties play a crucial role in many industrial applications. One of these properties is thermal expansion of steel or the tendency of steel to expand or contract with changes in temperature.

Thermal Expansion of Steel
Steel is an iron alloy that contains between 0.2% to 2.1% carbon by weight and is known for its high strength, hardness, and ductility. To enhance its properties, alloying elements can be added to steel. For example, chromium can be added for corrosion resistance, nickel can improve toughness and ductility, and molybdenum can enhance high-temperature strength.
Steel, like any other solid material, undergoes thermal expansion when heated and contraction when cooled. In the atomic level, thermal expansion can be explained by an increase in the average distance between the atoms as the material absorbs heat.
Temperature is a function of the average molecular kinetic energy of the atoms in a solid material. At higher temperatures, the atoms begin to vibrate and the interatomic distance between the atoms increase with the potential energy.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
This phenomenon is caused by the asymmetrical nature of the relationship between the potential energy and the interatomic distance, as shown in the diagram below:
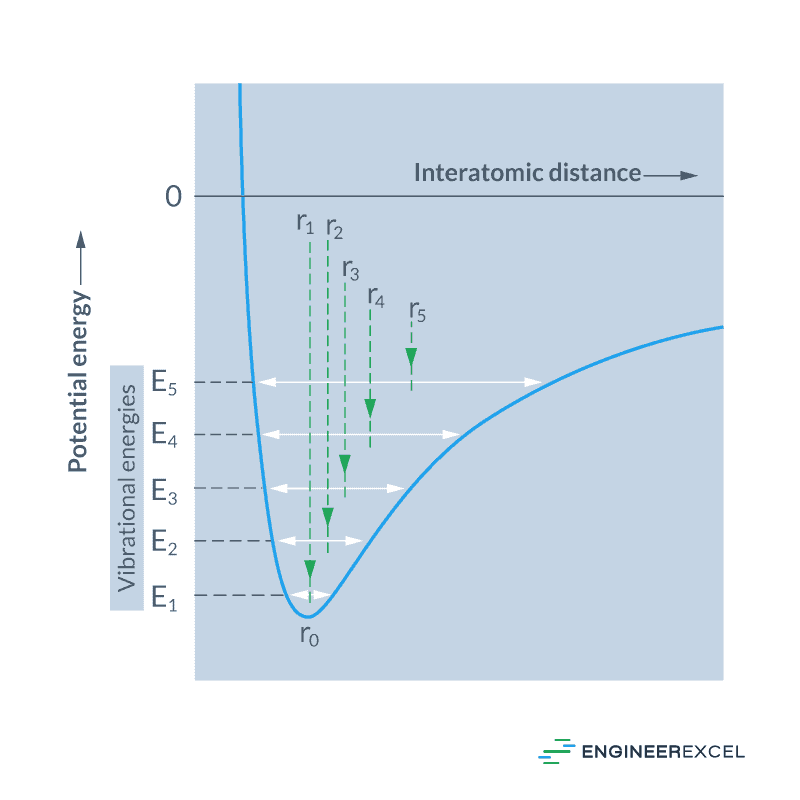
From the equilibrium position, when a material is heated to higher temperatures, the vibrational energy increases from E1 to E5. Consequently, because of the asymmetrical nature of the curve, the average spacing between atoms also increases, which can be observed by the mean positions, r1 to r5. This increase in the atomic spacing causes the steel to expand.
If the atomic bonding energy is high, the curve will be deeper and narrower. This means that the change in interatomic separation with a given change in temperature will be lower, yielding a smaller value of coefficient of thermal expansion.
Types of Thermal Expansion of Steel
The expansion or contraction of steel is proportional to its initial size, coefficient of thermal expansion, and the temperature change. Depending on which dimensions are considered important for a specific application, the thermal expansion of steel can be measured in three ways: linear, area, and volumetric.
Linear Thermal Expansion of Steel Formula
Linear thermal expansion refers to the change in length of a material in one dimension due to temperature change. This is illustrated in the diagram below:
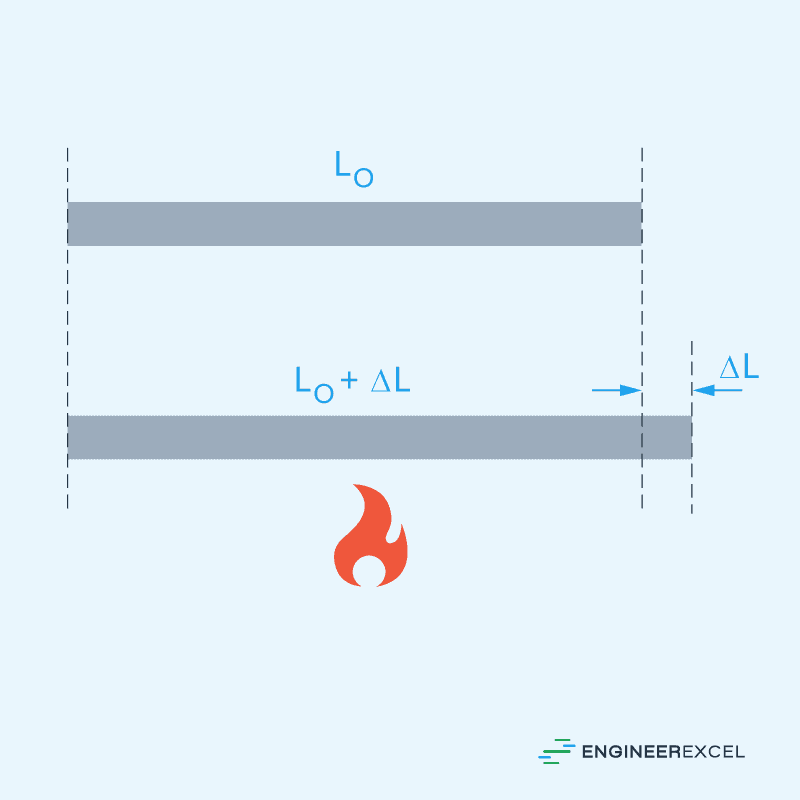
The change in length due to thermal expansion can be calculated using the formula:

Where:
- Δl = change in length of steel [m or in]
- l0 = initial length of steel [m or in]
- αl = linear coefficient of thermal expansion [K-1 or °F-1]
- ΔT = change in temperature [K or °F]
It is important to note that the formula above only applies to unrestrained steel— that is, if it is free to expand. Otherwise, if the steel specimen is restrained both ends, thermal expansion will cause stress to the material. This is illustrated in the diagram below:

The magnitude of the thermal stress developed by thermal expansion can be calculated using the formula:
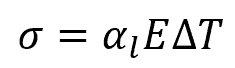
Where:
- σ = stress developed due to thermal expansion [Pa or psi]
- E = Young’s modulus of steel [Pa or psi]
Area Thermal Expansion of Steel Formula
Area thermal expansion refers to the change in the two-dimensional area of a steel specimen due to change in temperature. For specimens with holes, the holes also get larger with temperature because the proportions stay the same.
This is illustrated in the diagram below:
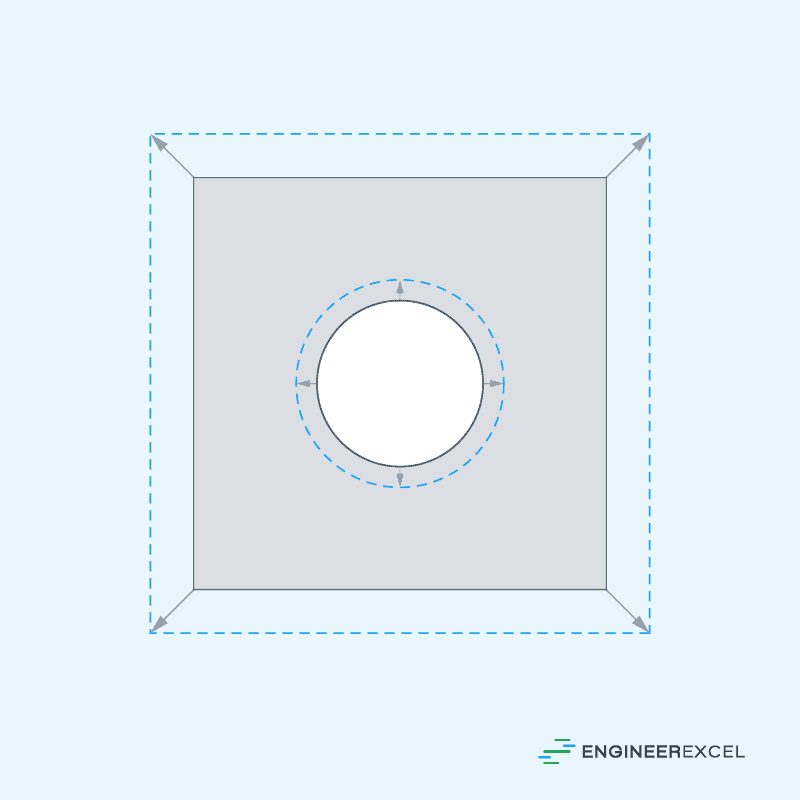
The change in area due to thermal expansion can be calculated using the formula:
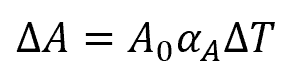
Where:
- ΔA = change in area of steel [m2 or in2]
- A0 = initial area of steel [m2 or in2]
- αA = area coefficient of thermal expansion [K-1 or °F-1]
For steels with isotropic thermal expansion, the area coefficient is approximately twice the value of the linear coefficient.
Volumetric Thermal Expansion of Steel Formula
In general, steel expands in all directions as temperature increases. Therefore, it is more conservative to consider the change in the volume of a steel specimen with respect to temperature.
This illustrated in the diagram below:
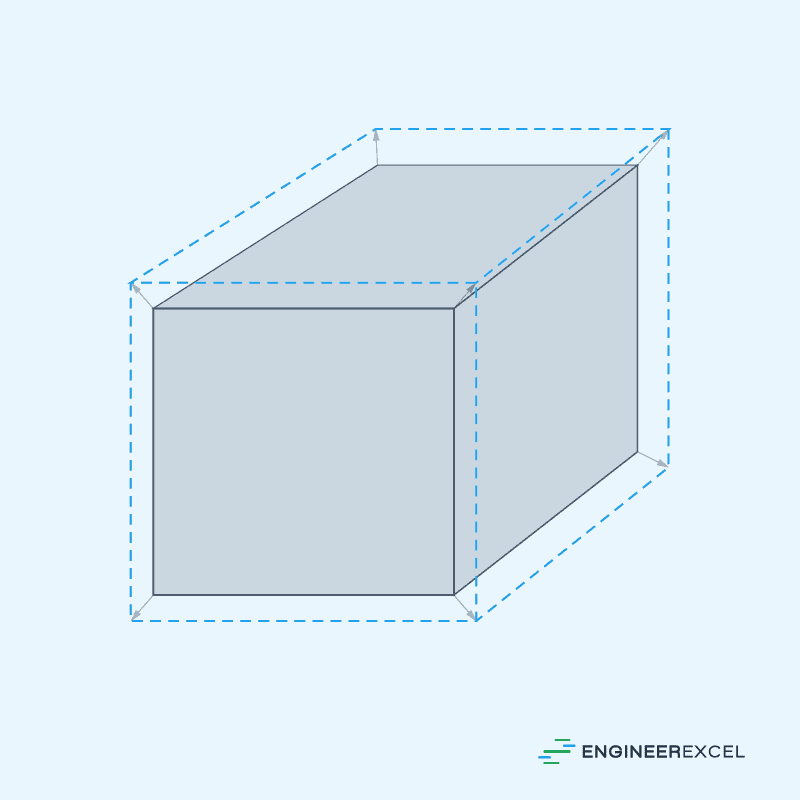
The change in volume due to thermal expansion can be calculated using the formula:
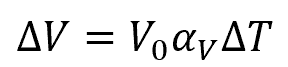
Where:
- ΔV = change in volume of steel [m3 or in3]
- V0 = initial volume of steel [m3 or in3]
- αV = volume coefficient of thermal expansion [K-1 or °F-1]
For steels with isotropic thermal expansion, the volume coefficient is approximately thrice the value of the linear coefficient.
Coefficient of Thermal Expansion of Different Types of Steel
The coefficient of thermal expansion is typically defined as the fractional increase in length per unit rise in temperature. While the value of this coefficient technically varies with temperature, in practice, most steels have coefficients of thermal expansion that remain relatively stable across the temperature ranges for which they are designed to be used. As such, for practical purposes where extremely high accuracy is not required, it is often sufficient to use an average, constant value for the coefficient of expansion in calculations.
The linear coefficients of thermal expansion for some of the most common plain carbon, low alloy, and stainless steels are shown below:
Coefficients of Thermal Expansion for Steel and Stainless Steel Alloys
Note that the values above are taken at room temperature. Typically, these values would slightly increase at higher temperatures.
For steels in which the thermal expansion is isotropic, the area coefficient and the volumetric coefficient are approximately twice and thrice the linear coefficient, respectively. These generally include unprocessed carbon and stainless steels.
However, in some types of steel, like cold-rolled, textured, and welded steel, the value of the coefficient is anisotropic; that is, it depends on the crystallographic direction along which it is measured. In addition, adding different alloying elements affect the coefficient of expansion. For example, several low-expansion iron alloys have been developed for applications requiring dimensional stability with temperature change, such as Invar and Kovar.
Importance and Applications of Thermal Expansion of Steel
Understanding thermal expansion is crucial when dealing with steel in applications that experience temperature changes. For example, in designing steel structures, it is important to consider the expansion and contraction of the steel components in order to ensure safety across the extreme operating conditions.

Even though there may not be any moving component, structural components may experience fluctuating thermal stresses and fatigue induced by temperature variations. This is the reason why large structures, including buildings, bridges, and pipelines, typically incorporate expansion joints in the design to give room for expansion and prevent stress, thereby extending the lifespan of the structure.
Aside from safety reasons, the thermal expansion of steel also has practical applications in various industries. For instance, the principle of thermal expansion is utilized in temperature sensors that measure temperature changes through a small piece of steel that acts as a temperature-sensing element. As the temperature fluctuates, the steel expands or contracts, resulting in a change in its electrical resistance that can be quantified and used to determine the temperature.
Bimetallic strips are another practical application of thermal expansion used in thermostats. These strips contain two different metals with unique coefficients of thermal expansion. When heated or cooled, one metal expands or contracts more than the other, causing the strip to bend, which can be measured in relation to temperature.
