The area moment of inertia is a fundamental concept in solid mechanics that measures a shape’s resistance to bending or deformation. It is particularly important in structural engineering when analyzing beams subjected to bending moments.

In this article, we will discuss the definition of the area moment of inertia, how to calculate it for different geometries, and how to apply the Parallel Axis Theorem to find the moment of inertia around a different axis.
What is the Area Moment of Inertia?
The area moment of inertia, also known as the second moment of area, is a property of a shape that measures its resistance to bending or deformation. It plays a significant role in structural engineering, especially in analyzing beams subjected to bending moments.
The area moment of inertia depends on the shape and distribution of material about an axis—usually the centroidal axis of the shape. Hence, it is calculated with respect to a given axis and is defined as the integral of the square of the distance from each infinitesimal element of area to the axis of rotation.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
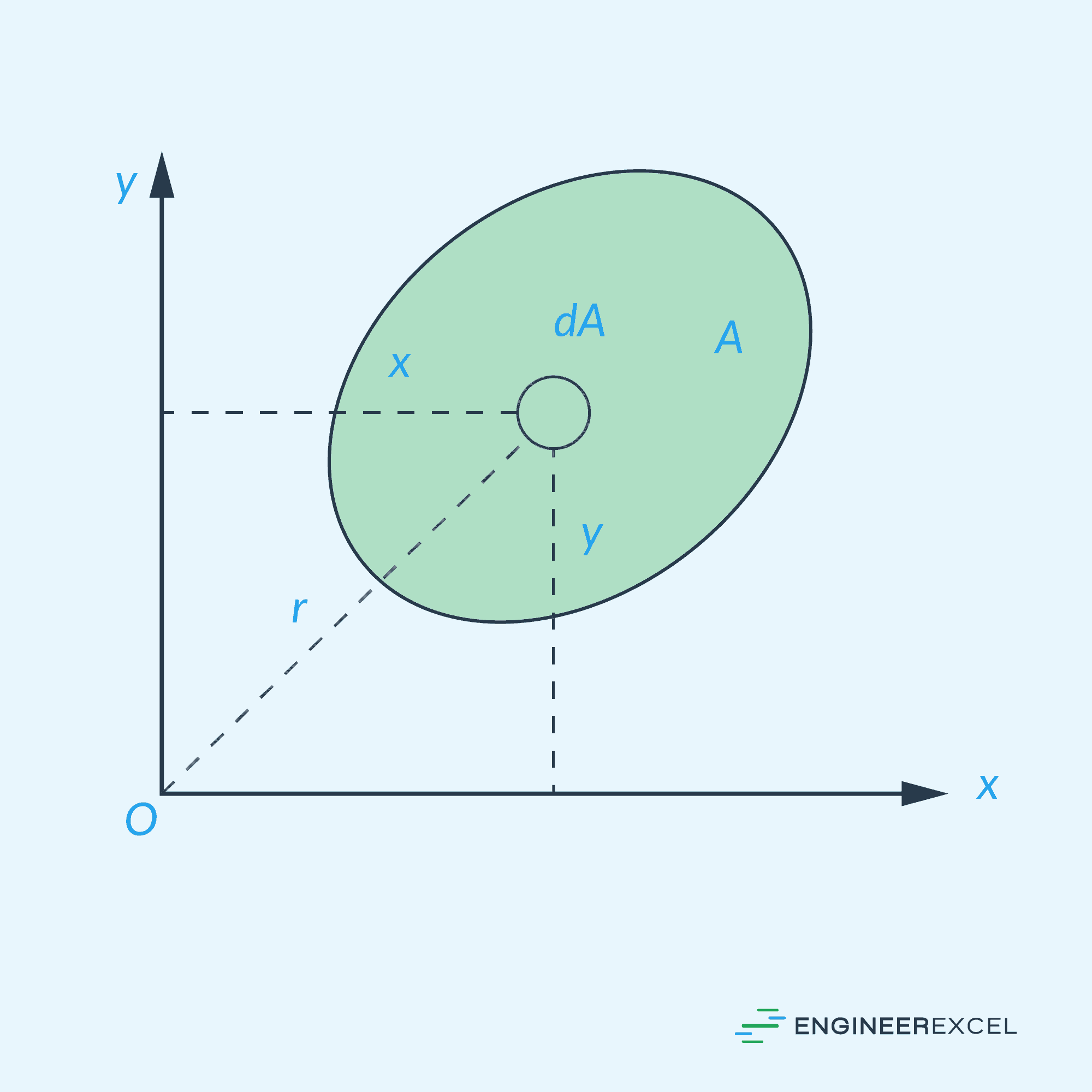
To give an example, consider the oval shape below:

The oval’s area moment of inertia about the axis O-O can be calculated using the following formula:
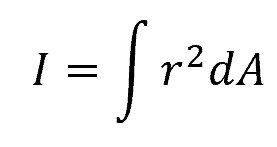
Where:
- I = area moment of inertia with respect to the axis [m4]
- r = distance from the axis of rotation to an infinitesimal area element dA [m]
- dA = an infinitesimal area element [m2]
Alternatively, in a rectangular coordinate system, the area moment of inertia about the x and y axes can be calculated using the following formulas:
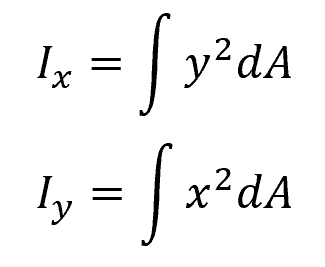
Where:
- Ix, Iy = area moment of inertia with respect to the x and y axes, respectively [m4]
- x, y = distance of an infinitesimal area element dA from the y and x axes, respectively [m]
We can also calculate the area moment of inertia about the pole. This is known as the polar moment of inertia:
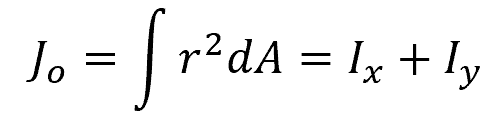
Where:
- Jo = polar moment of inertia [m4]
- r = distance of an infinitesimal area element dA from the pole [m]
Notice that the polar moment of inertia is simply the sum of the area moments of inertia in rectangular coordinates.
In structural engineering, high values for the area moment of inertia are desirable for structural members, as this property determines the stiffness and resistance to bending. A greater moment of inertia enables the beam or structural member to withstand higher bending forces without significant deformation. Careful consideration of the area moment of inertia in design helps in enhancing structural integrity and overall performance.
Calculating the Area Moment of Inertia of Common Shapes
For homogeneous materials and standard shapes, such as rectangles, circles, and I-beams, the area moment of inertia about the centroid can be found using standard formulas. These are listed in the table below.

Parallel Axis Theorem
Calculating the area moment of inertia around the centroidal axis of common shapes is easy with readily available formulas. However, sometimes it’s necessary to find the area moment of inertia around a different axis. This is where the Parallel Axis Theorem comes in handy.
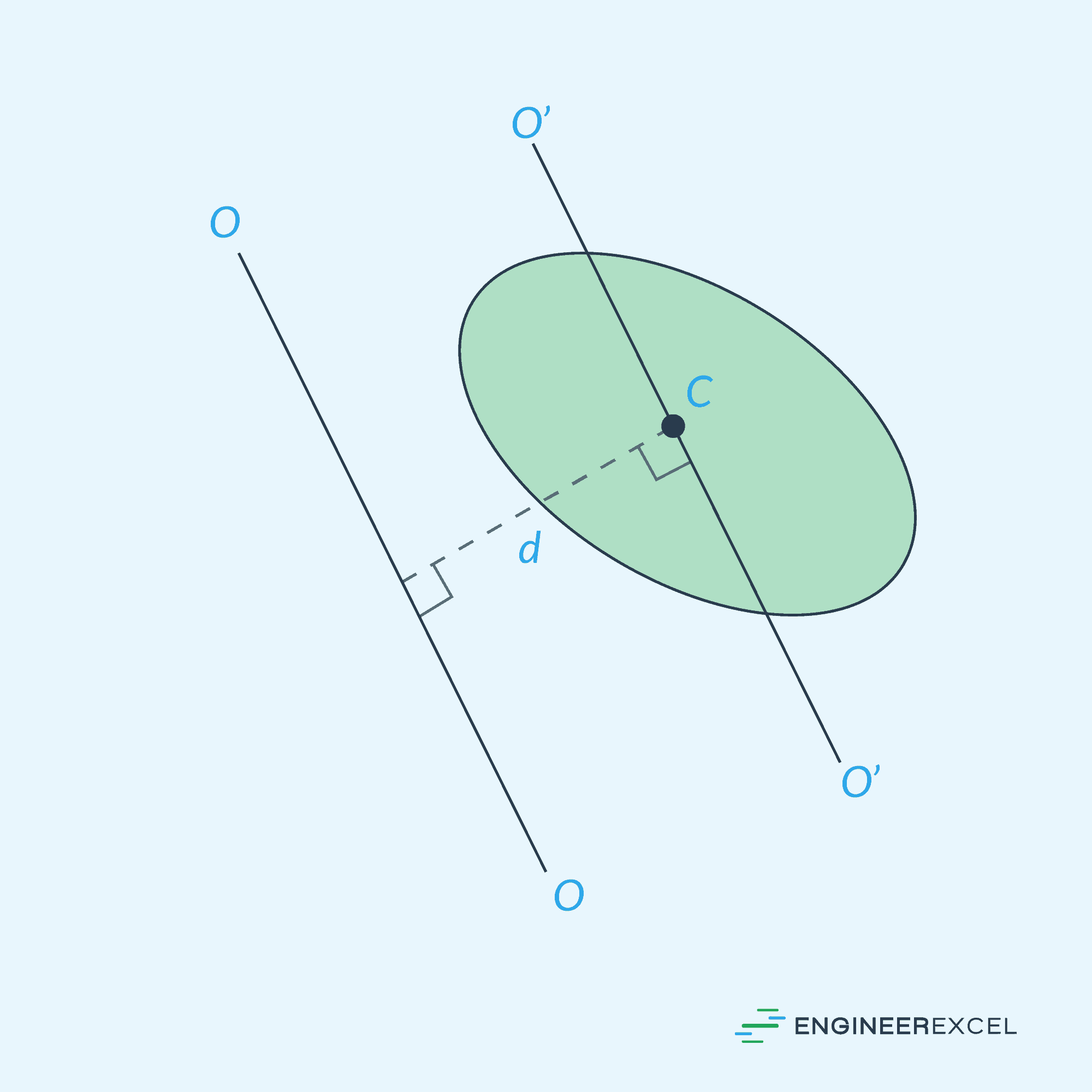
The Parallel Axis Theorem enables us to determine the moment of inertia of an object relative to an axis parallel to the centroidal axis but not coincident with it. The formula for the area moment of inertia using the Parallel Axis Theorem is:
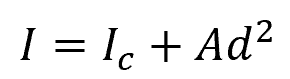
Where:
- I = moment of inertia around the parallel axis [m4]
- Ic = moment of inertia around the centroidal axis [m4]
- A = area of the shape [m2]
- d = distance between the two axes [m]
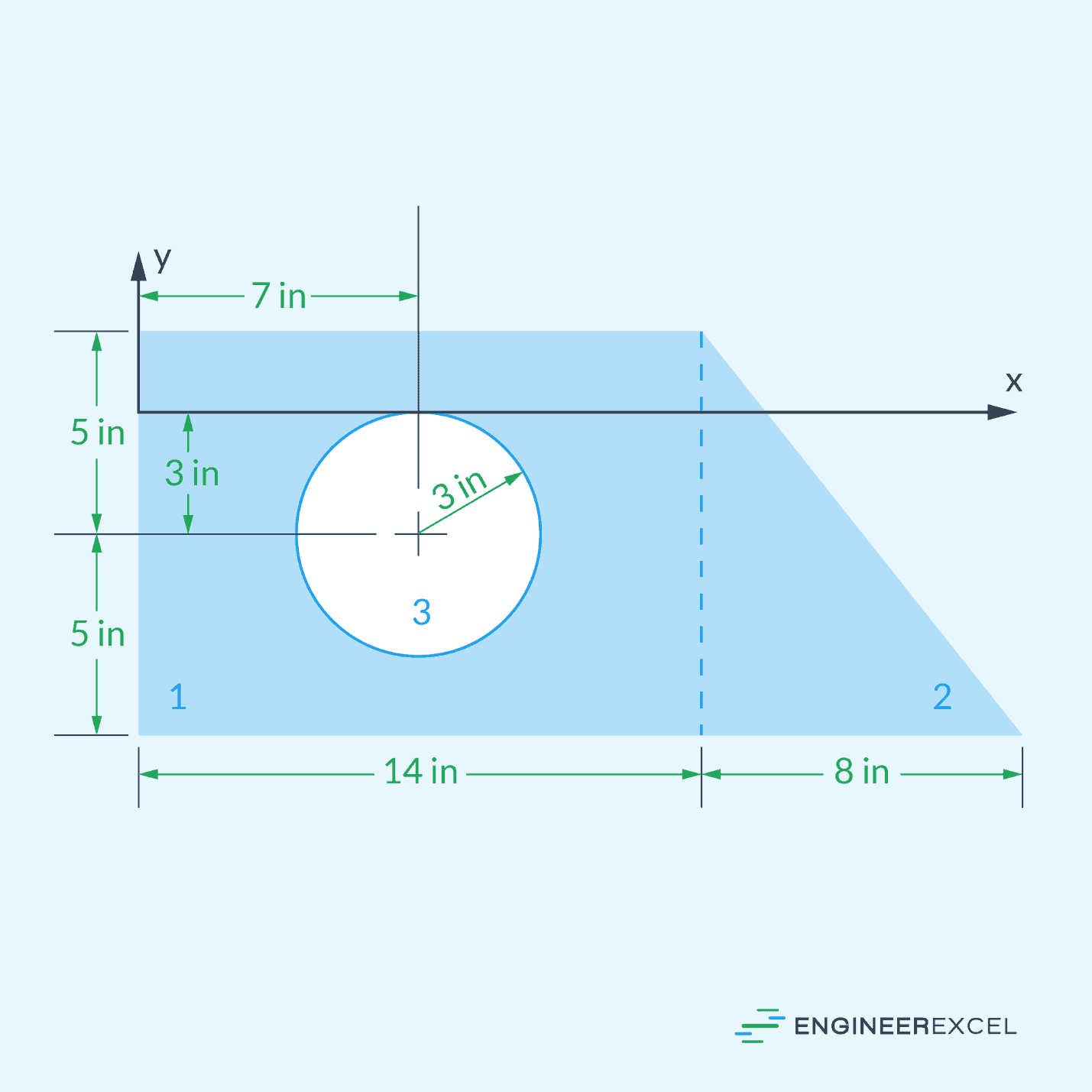
Calculating the Area Moment of Inertia of Composite Bodies
Calculating the area moment of inertia for composite bodies is more complex due to the combination of multiple shapes. To simplify the process, break down the geometry into smaller shapes and sum up their respective moments of inertia about the same axis. This is normally done by applying the Parallel Axis Theorem to shift each moment of inertia to a common reference axis.
For a composite shape made up of subparts, the moment of inertia of the whole shape is the sum of the moments of inertia of the individual parts, with the moment of inertia of any holes subtracted from the total of the positive areas. For example, for the composite body shown below, the area moment of inertia of the circular section is subtracted from the sum of the area moments of inertia of the rectangular and triangular sections.