The moment of inertia (or area moment of inertia) of an object is an expression of that object’s tendency to resist bending. The moment of inertia is extensively employed in engineering as a structural parameter. When designing a structure, an engineer will apply the moment of inertia to optimize the design with respect to expected loads.
An I beam is a common structural member, and calculating its moment of inertia can be broken down into three specific steps, as follows.
I-Beam Moment of Inertia
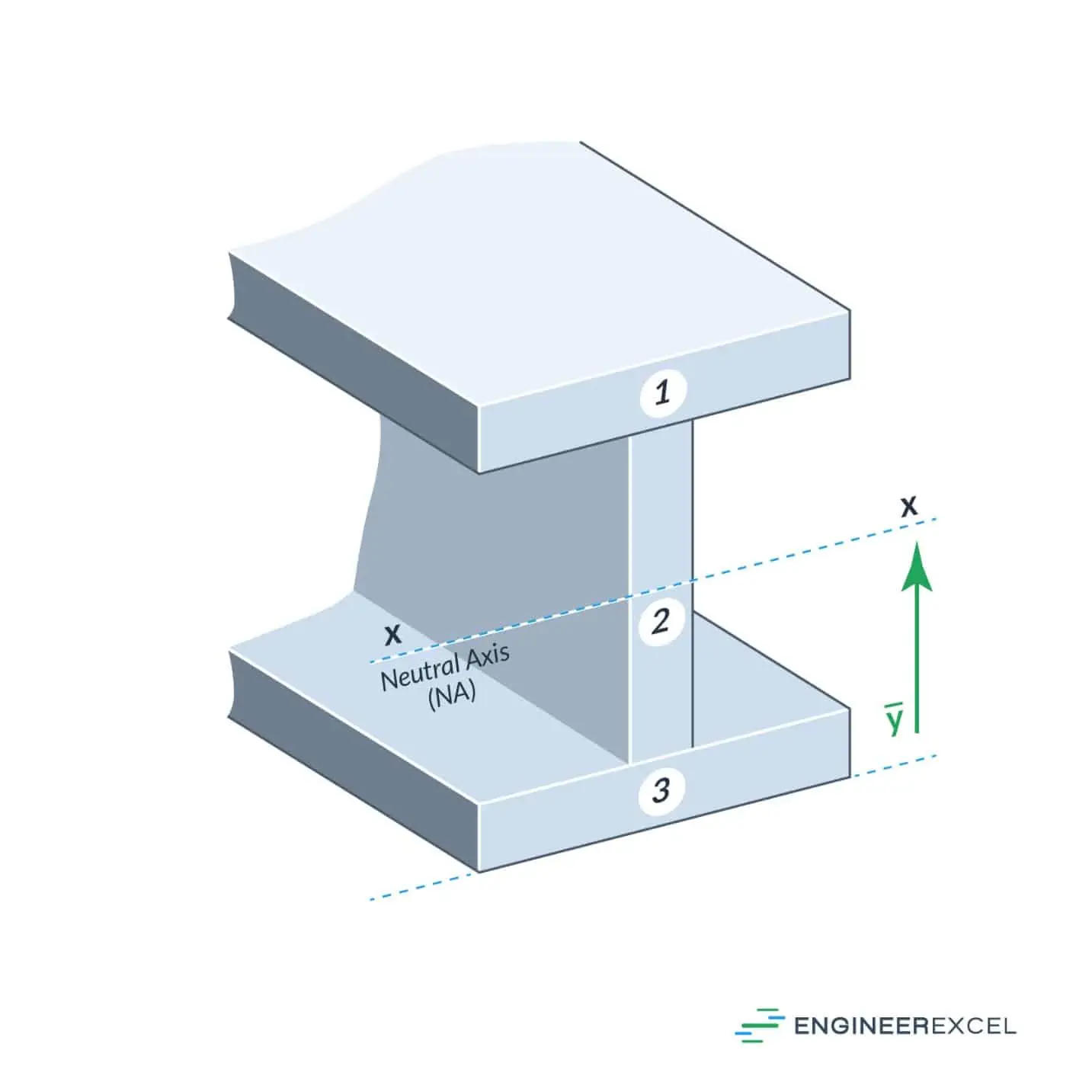
The first step for calculating the moment of inertia of an I beam is to segment the beam into smaller parts. In this case, the beam is divided into three sections, as shown in the figure below:

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
The moment of inertia of the beam can be calculated by determining the individual moments of inertia of the three segments.
Find The Neutral Axis
The moment of inertia will be about the neutral axis, which passes through the center of mass. The neutral axis is marked in the above figure, and the location of the center of mass can be calculated as follows:
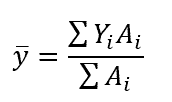
where Yi is the center of mass of an individual rectangle, with SI units of m, and Ai is the area of an individual rectangle, with SI units of m2. In the case of the I beam, i is from 1 to 3.
Calculating The Moment Of Inertia
The parallel axis theorem is used to determine the total moment of inertia of the I beam as follows:
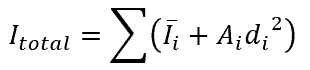
where is the moment of inertia of an individual rectangle, with SI units of m4, and di is the distance from the centroid of an individual rectangle to the centroid of the I beam, with SI units of m.
The individual moments of inertia are calculated for the rectangles using the following formula:

where b is the base of the rectangle and h is the height of the rectangle, both with SI units of m.
Moment Of Inertia About The Y-Axis
Generally, I beams are designed to be symmetric about the y-axis. That is, the moment of inertia of an I beam about the y-axis is about the center of beam.
I-Beam Moment of Inertia Example
The following I beam is used as an example for calculating the moment of inertia:
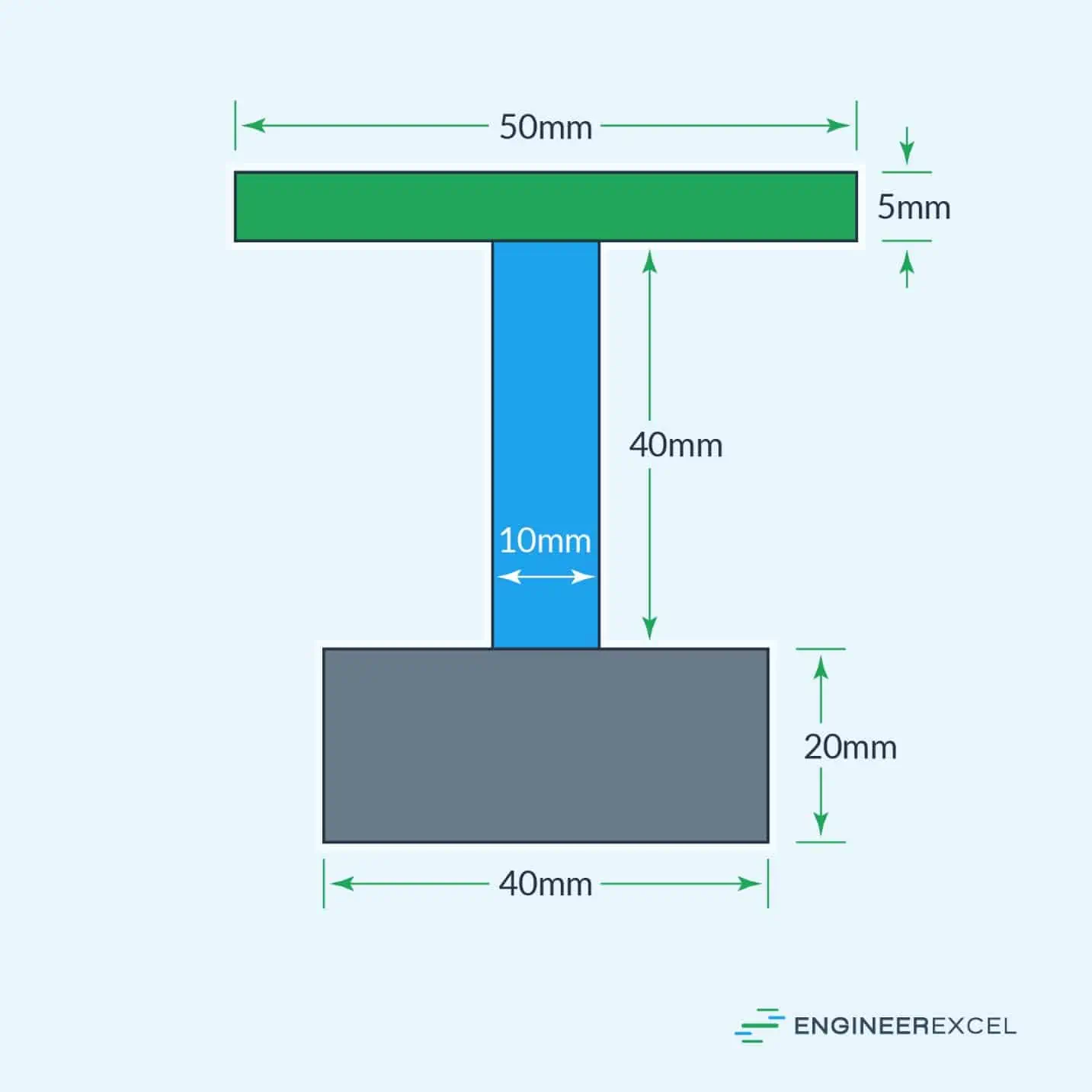
Segment The Beam
The above beam has been segmented into three sections, green, yellow, and blue, which are designated sections 1, 2, and 3, respectively.
Find The Neutral Axis
The neutral axis passes through the center of mass, which is calculated as follows:
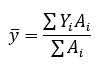
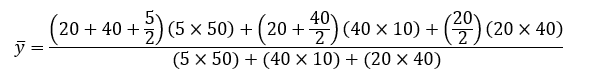
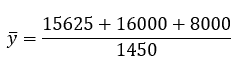
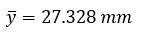

Calculate The Moments Of Inertia
The individual moments of inertia of the three segments are calculated using the moment of inertia formula for a rectangle:
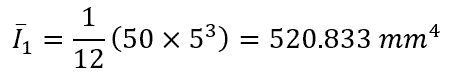
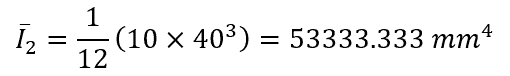
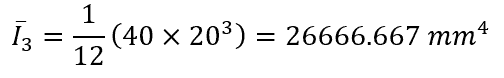
Apply The Parallel Axis Theorem
For each segment, the parallel axis theorem is applied:
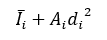
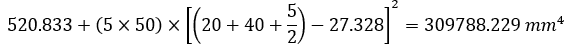
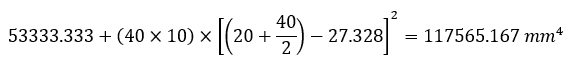
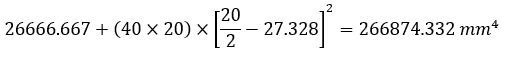
Sum Individual Moments Of Inertia
Summing the individual moments of inertia of the three sections:
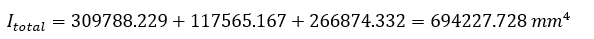
Applying The Moment Of Inertia Of I Beams

I beams are common engineering structural elements. Not only are they used as components of engineering designs, but may also be used as simulative elements for preliminary design of things like aircraft wings. Although most I beams have a symmetrical layout, it is possible for a beam to be asymmetric about the x-axis, as in the previous example. For an I beam that is symmetrical, the moment of inertia about the x-axis will be located at the physical center of the beam, similar to the moment of inertia about the y-axis, as previously discussed.
