Water displacement refers to the phenomenon where an object immersed in water pushes the fluid aside to make space for itself. This concept is central to various fields, especially naval architecture, and relies on fundamental principles such as Archimedes’ Principle and the concept of buoyancy. In this article, we will discuss the concept of water displacement, how it is measured, and its applications in engineering.
Water Displacement Explained
According to Archimedes’ Principle, when an object is submerged in water, the water displaced by the object causes the object to experience an upward buoyant force equal to the weight of the water displaced. This is illustrated in the diagram below.
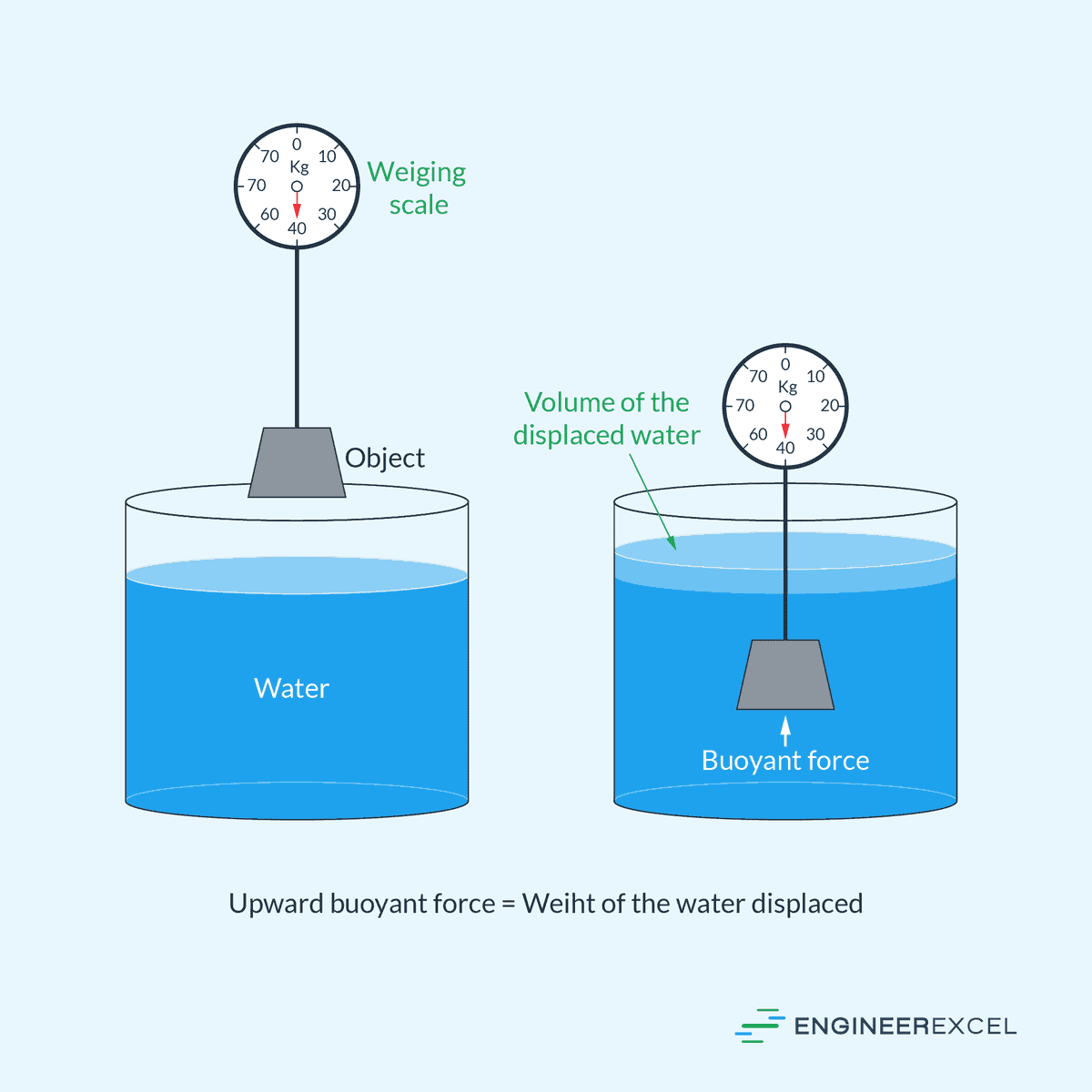
This can be formulated mathematically as:
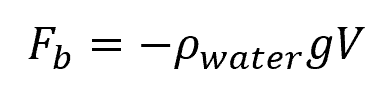

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
Where:
- Fb = buoyant force [N]
- Ρwater = density of the water displaced [kg/m3]
- g = acceleration due to gravity [9.81 m/s2]
- V = volume of the water displaced [m3]
The negative sign indicates that the buoyant force acts opposite of the weight of the object.
Archimedes’ principle plays an important role in determining whether an object will float or sink when placed in a fluid. If the buoyant force is greater than the object’s weight, it will float. On the other hand, if the buoyant force is less than the object’s weight, the object will sink.
If the buoyant force matches the object’s weight, it will remain suspended at its current depth. However, the extent to which a floating object is suspended depends on the relative densities between the object and the fluid, as shown by the following equation:
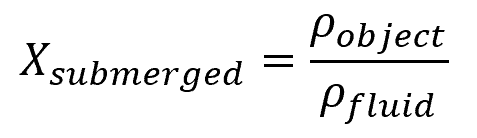
Where:
- Xsubmerged = fraction of the object submerged in the fluid [unitless]
- ρobject = density of the object [kg/m3]
Therefore, buoyancy itself is contingent upon the object’s density relative to the fluid. An object less dense than the fluid will float, while a denser object will sink.
It is important to note that the buoyant force is consistently present, regardless of whether the object floats, sinks, or remains suspended in a fluid. Engineers exploit this principle when designing ships and submarines, ensuring the structures displace enough water to create a buoyant force counteracting their weight.
Measuring Water Displacement
There are many ways to measure water displacement. The two most common ways are the Volumetric Method and the Weigh-In Method.
Volumetric Method
The Volumetric Method involves submerging an object in water within a graduated container and observing the water level rise. This method rests on the principle that the submerged object will displace a volume of water precisely equal to the object’s volume.
To do this, fill a container with a known volume of water, marking the initial water level. Then, gently submerge the object without splashing to avoid measurement errors. Record the new water level; the difference between initial and final water levels indicates the volume of water displaced, hence the volume of the object.
Weigh-In Method
The Weigh-In Method, alternatively, utilizes the object’s mass difference before and after submersion. To do this, place the object on a scale to determine its initial mass in air. Then, submerge the object fully in water and measure the apparent mass in water.
The water displacement volume can be calculated using the following relationship:
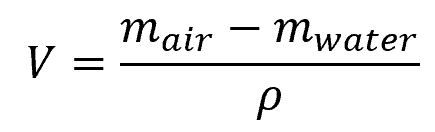
Where:
- mair = mass of the object in air [kg]
- mwater = apparent mass of the object in water [kg]
Applications in Engineering
Water displacement is an essential consideration in various engineering disciplines, most notably in marine engineering where it governs the buoyancy and stability of structures like ships and submarines. This section explores how engineers account for and utilize the principles of water displacement in ship and submarine design, as well as in analyzing fluid flow.
Ship Design
In ship design, water displacement is directly tied to a vessel’s buoyancy, which is the force that allows it to float. Engineers must carefully calculate the displacement of water to design a ship’s hull shape, ensuring it can displace enough water to support the weight of the ship and its cargo. They must also consider the distribution of weight within the ship to maintain stability and prevent capsize.
Submarine Design
Unlike surface ships, submarines must operate underwater and control their buoyancy to ascend and descend as needed. This is achieved by adjusting the water volume within ballast tanks. Filling the tanks with water increases displacement and causes the submarine to sink, while expelling water from the tanks reduces displacement, allowing it to rise.
Fluid Flow Analysis
Engineers employ computational fluid dynamics (CFD) tools to simulate how water flows around objects, such as bridge piers or offshore platforms. These simulations help engineers to predict and minimize potential problems caused by water displacement, such as scour, which can erode the foundations of such structures. Fluid flow analysis also aids in optimizing the shape and materials of engineering projects to reduce drag and improve stability when interacting with water.
Example Problem
Problem: A cylindrical object with a radius (r) of 0.5 m and a height (h) of 2 m is fully submerged in a container of water. What is the buoyant force acting on the object?
Solution: To find the buoyant force acting on the cylindrical object, we must first find the volume of water displaced by the object. Knowing that the object is fully submerged, we can find this using the formula:
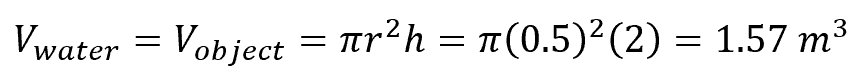
Now we can find the buoyant force, which is equal to the weight of the water displaced. Assuming the density of water is 1000 kg/m3, the formula becomes:
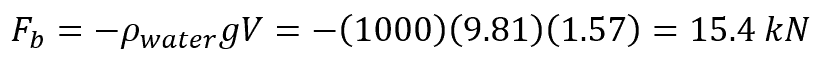
Therefore, the buoyant force acting on the object is 15.4 kN.
