The center of buoyancy is the centroid of the displaced volume of fluid by a submerged or floating object. It represents the point at which the upward buoyant force acts on the object, counteracting the force of gravity.

In this article, we will discuss the concept of the center of buoyancy, its significance in various practical applications, and how factors like load distribution and water density affect its movement.
What Is The Center Of Buoyancy?
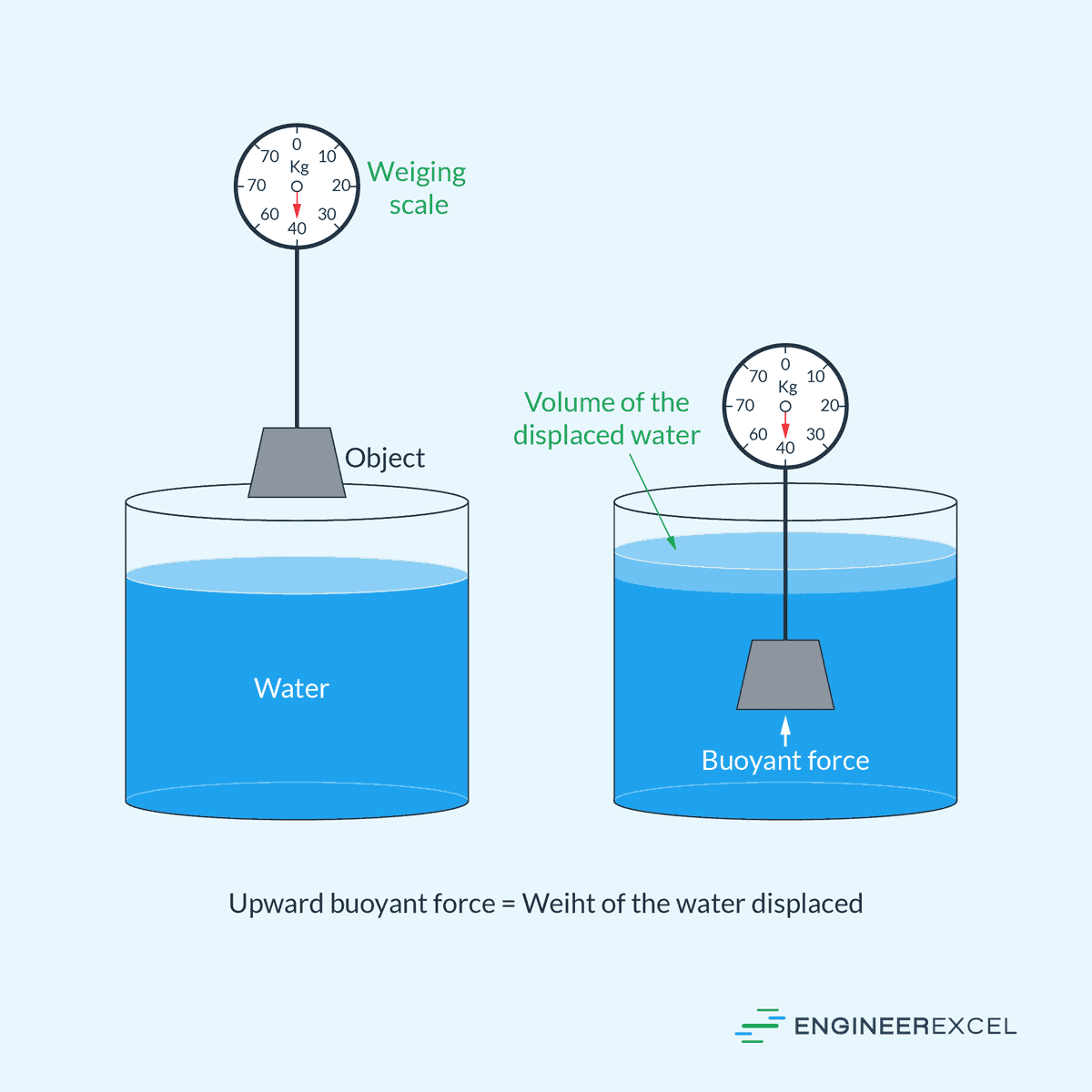
Archimedes’ principle states that a body submerged in a fluid experiences an upward buoyant force equal to the weight of the fluid displaced by the body, as illustrated in the diagram below.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
The magnitude of this buoyant force can be calculated as follows:
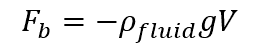
Where:
- Fb = buoyant force [N]
- ρfluid = density of the fluid displaced [kg/m3]
- g = acceleration due to gravity [9.81 m/s2]
- V = volume of the fluid displaced [m3]
The equation above shows that the buoyant force increases with the volume and density of the displaced fluid. Furthermore, the negative sign indicates that the buoyant force opposes the weight of the body.

The point where this buoyant force acts is called the center of buoyancy, as shown in the diagram above. This point is typically located at the center of volume of the displaced liquid.
It is important to note that the center of buoyancy may not always align with the actual center of gravity of the body’s material, especially if the material has varying density or is not fully submerged. However, for homogeneous materials that are fully submerged, the center of gravity and the center of buoyancy coincide.
The stability of a submerged object is affected by the relative positions of the center of buoyancy and the center of gravity. When an object is stable and at rest in a fluid, the center of gravity and the center of buoyancy are vertically aligned. However, if the object tilts or shifts, the center of buoyancy moves in relation to the object’s geometry.
In general, stability increases when the center of buoyancy is located above the center of gravity.
Center of Buoyancy in Non-Homogeneous Fluids
In non-homogeneous, layered fluids, the buoyant force can be obtained by summing the weights of each layer of density displaced by the immersed body, as shown in the following equation:
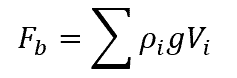
Where:
- ρi = density of each layer of fluid displaced [kg/m3]
- Vi = volume of each layer of fluid displaced [m3]
In this case, each displaced layer would have its own center of volume. To determine the center of buoyancy of the immersed body, we need to sum the moments of the incremental buoyant forces.
Practical Applications
Ship Design
In ship design, the center of buoyancy is the geometric center of the underwater volume of the ship’s hull and is pivotal in maintaining the vessel’s equilibrium. As a ship is heeled over by external forces, the body is tilted a small angle and the center of buoyancy shifts laterally. A vertical line drawn from the new center of buoyancy intersects the line of symmetry at a point called the metacenter.
The relationship between the center of gravity and the metacenter determines the ship’s stability. If the metacenter is above the center of gravity, a restoring moment is present and the original position is stable. Otherwise, the body is unstable and will overturn if disturbed.
The higher the distance between the metacenter and the center of gravity, the greater the ship’s ability to right itself. However, excessive height can lead to a more rapid and pronounced recovery, which can be uncomfortable for passengers and crew. Therefore, a balance must be maintained for optimal stability.
Submarine Ballast Systems
The center of buoyancy is also essential in the design and operation of submarine ballast systems. Submarines achieve buoyancy control through the use of ballast tanks, which can be filled with water to increase weight or with air to decrease it. The careful management of these tanks allows a submarine to maintain, lose, or gain buoyancy, which in turn affects its depth in water.
When submerged, the center of buoyancy must be carefully aligned with the center of gravity to ensure that the submarine remains stable under different operational conditions. An imbalance may cause the submarine to pitch or roll uncontrollably.
Floating Structures
For floating structures like oil platforms and floating docks, the center of buoyancy ensures that these large and often immobile constructions remain stable on the water surface. These structures are typically engineered to have a low center of gravity and a broad base to maximize the buoyant force received from the displaced water. Their design must also account for various environmental factors, such as tides and waves, which could alter the center of buoyancy and threaten the stability of the structure.
Movement Of Center Of Buoyancy
The center of buoyancy is the focal point where the upward force of buoyancy, which counteracts gravity, acts on a submerged body. It shifts depending on changes in the body’s geometry or position and is affected by load distribution and water density.
Effect Of Load Distribution
When a vessel’s load is altered, either by addition or redistribution of weight, the center of buoyancy moves in response. Uniform loading tends to keep the center of buoyancy relatively stationary, whereas non-uniform or asymmetric loading can cause it to shift towards the heavier side. For example, if weight is added to the starboard side of a ship, the center of buoyancy will move starboard.
Impact Of Water Density Changes
The center of buoyancy can also be influenced by changes in the density of the water in which the body is immersed. A body’s buoyancy is proportionate to the volume of water it displaces, which correlates to water density.
In denser water, a vessel floats higher, causing the center of buoyancy to move upward in the vessel. Conversely, in less dense water, the vessel sinks lower, shifting the center of buoyancy downward. This effect is important to consider for vessels transitioning from freshwater to saltwater or vice versa, as salinity levels affect water density significantly.
