In physics and engineering, work is defined as the transfer of energy associated with the action of a force. When evaluated on a per unit mass basis, work done on or by the substance is called specific work.

In this article, the concept of specific work is discussed in detail, including its definition and formula across a range of applications.
Specific Work Explained
Specific work is defined as the amount of work done per unit mass of substance. Hence, it can be defined and analyzed the same way as work, but on a per unit mass basis. This approach is especially helpful in thermodynamics and fluid mechanics, where the energy terms involving fluid flow are usually written as energy per unit mass.
Just like work, the specific work can be positive, negative, or zero, depending on the direction of the work done. There are differing sign conventions for this, depending on how the conservation of energy equation is written. In physics and engineering applications, the conservation of energy equation is written as:

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
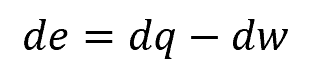
Where:
- de = change in energy of the system per unit mass [J/kg]
- dq = net heat added per unit mass [J/kg]
- dw = net work done by the system per unit mass [J/kg]
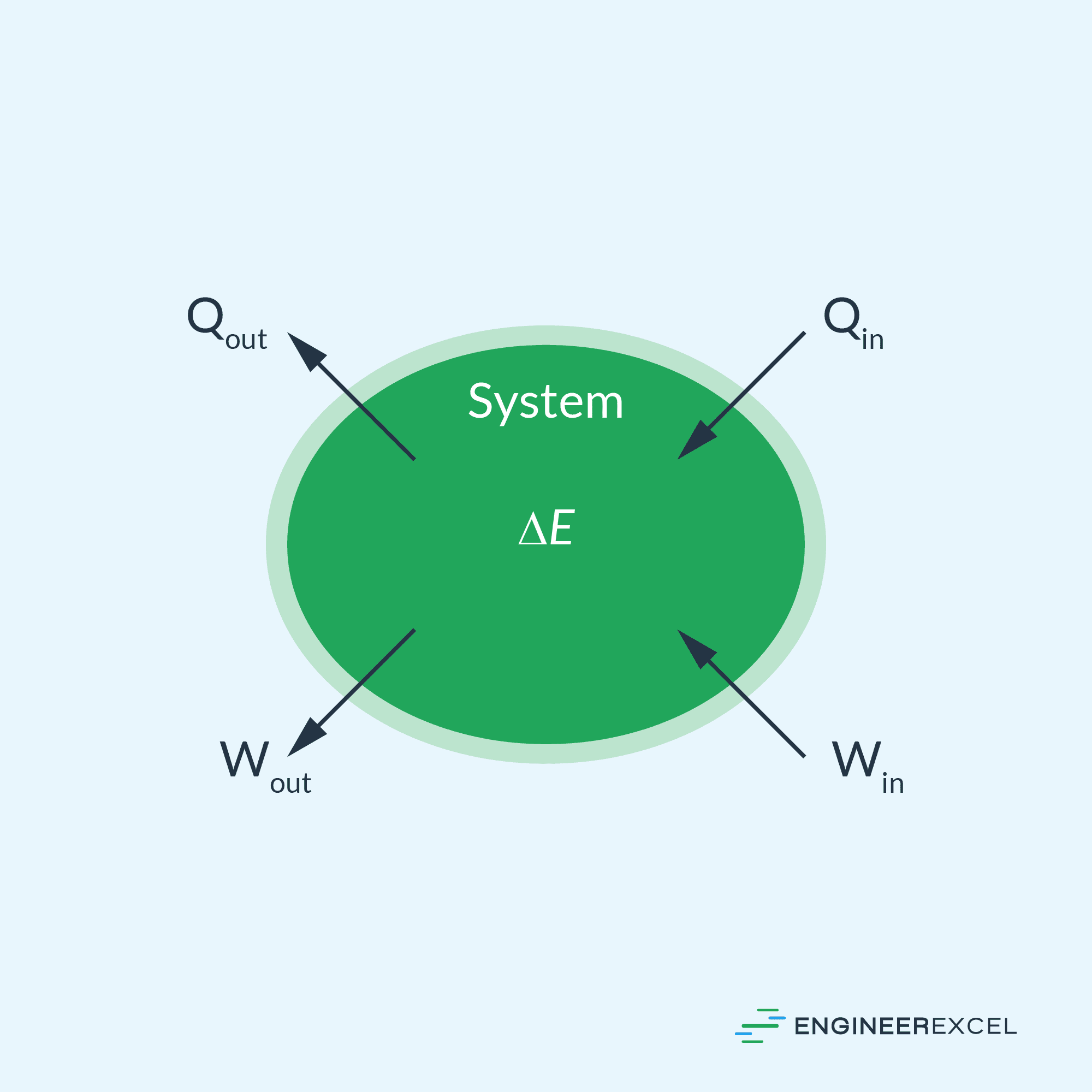
Following this form of energy equation, specific work done by the system on the surroundings is regarded as positive, while specific work done on the system by the surroundings is negative.
On the other hand, heat added to the system is positive, while heat removed from the system is negative.
Formula for Specific Work
Work can result from various forces such as pressure and body forces acting alone or in combination. The formula for calculating the specific work depends on the type of forces present in the system.
Specific Work Resulting from Body Force
In its simplest form, specific work resulting from the action of a force can be written as:
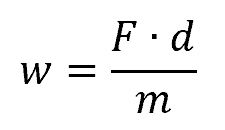
Where:
- w = specific work [J/kg]
- F = constant force acting on the substance [N]
- d = displacement of the substance [m]
- m = mass of the substance [kg]
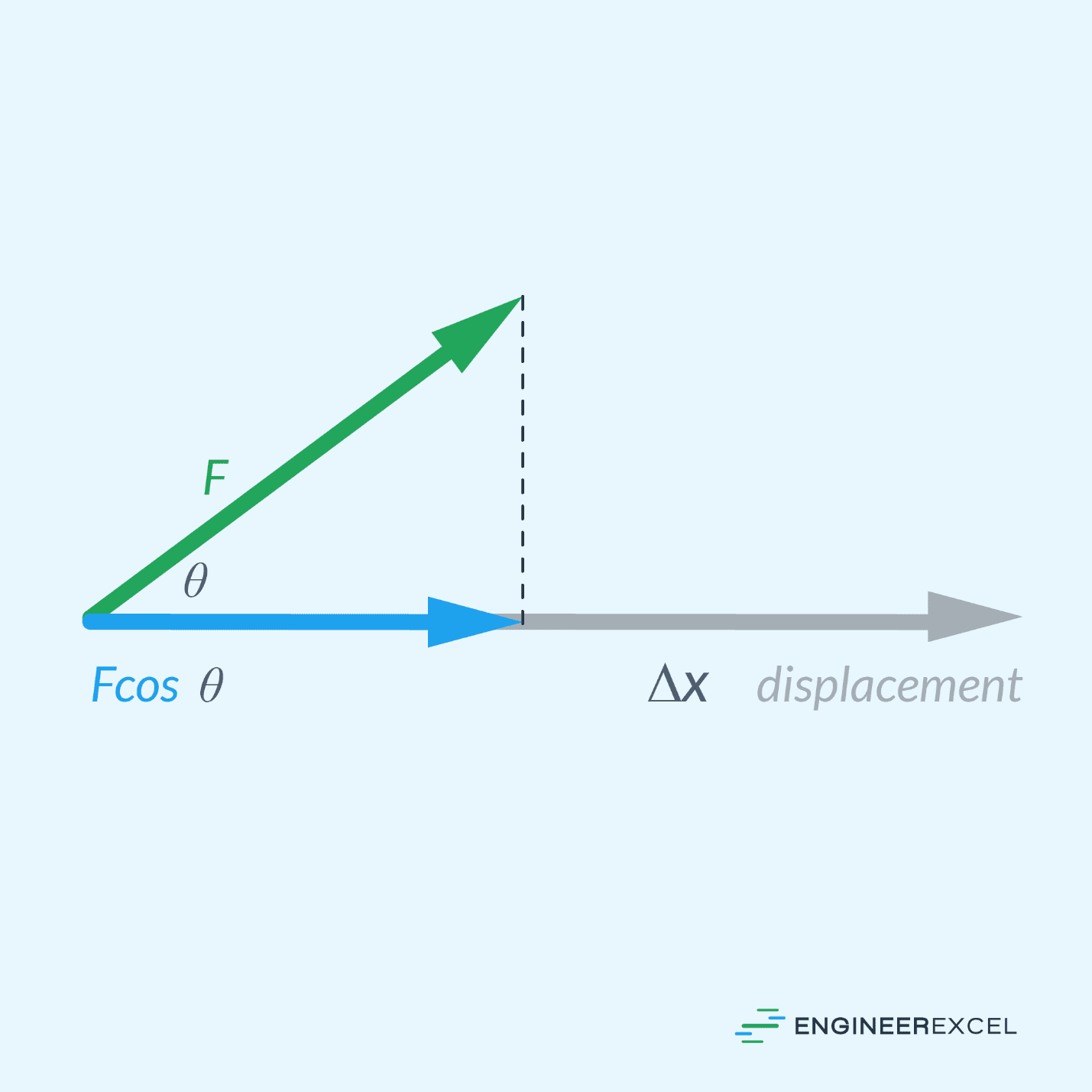
Note that force and displacement are vector entities and work is a scalar quantity equal to the dot product of the two. Hence, for a pair of non-parallel force and displacement vectors, the formula for specific work becomes:
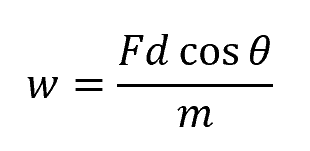
Where:
- θ = angle between the force and displacement vectors [degrees or radians]
A more general form for calculating specific work can be obtained by assuming a variable force acting on an object, whose magnitude is a function of the object’s position. In this case, the formula for specific work becomes:
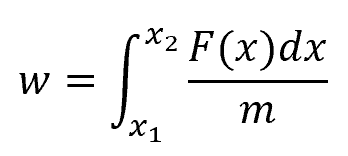
Where:
- F(x) = force as a function of x [N]
- x1 and x2 = initial and final position of the object [m]
Specific Work Resulting from Torque
For a torque acting on a body, the formula for specific work becomes:
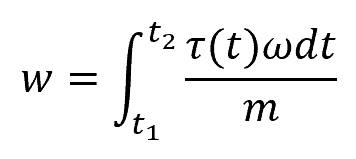
Where:
- τ(t) = torque as a function of time [N-m]
- ω = angular velocity [rad/s]
- t1 and t2 = initial and final time [s]
Specific Work Resulting from Pressure
In most fluid systems, work is done by pressure. In this case, a pressure force arises from the pressure acting over an area. To illustrate, consider a piston-cylinder system, shown below.
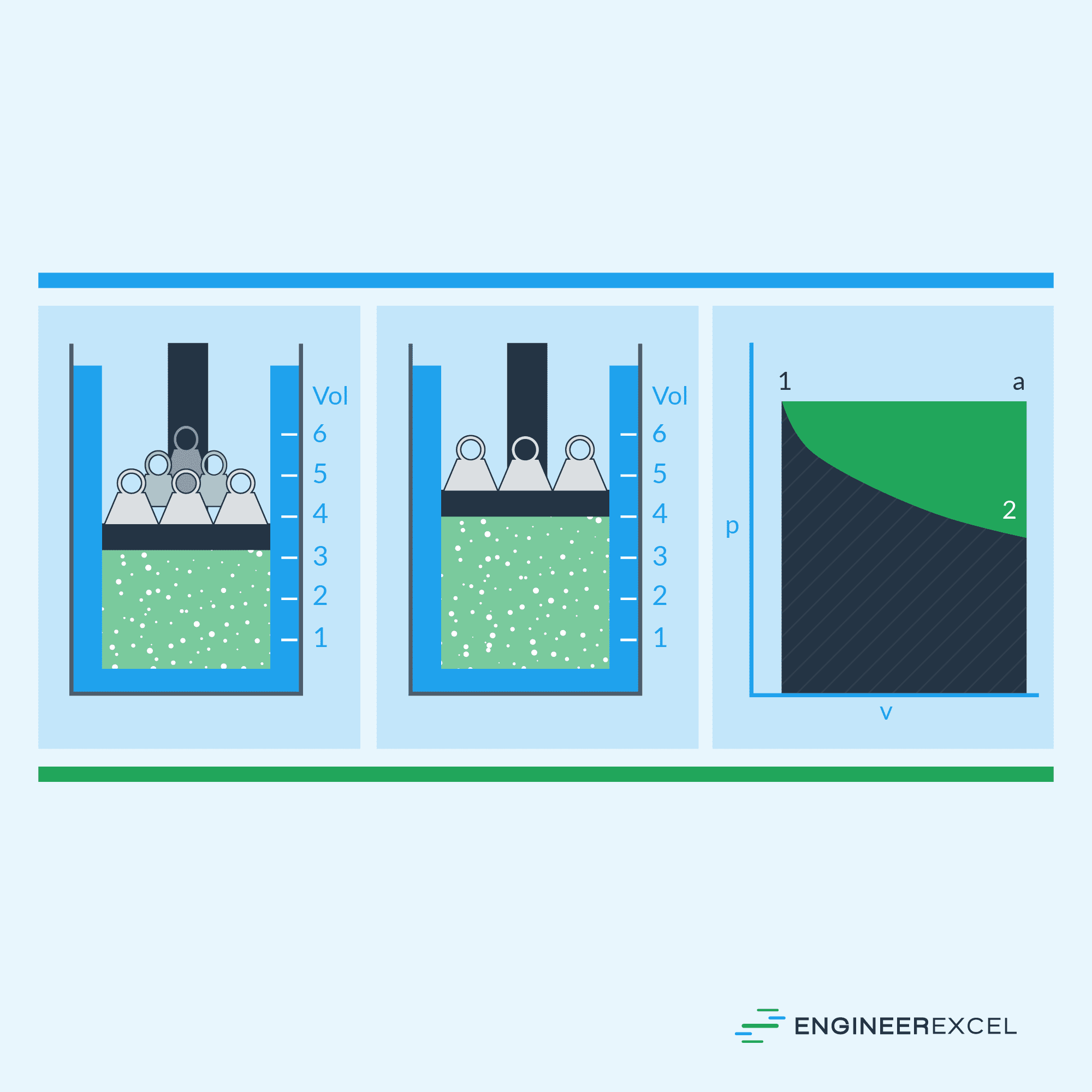
As shown in the diagram, the fluid expands from State 1 to State 2, resulting in an increase in volume and a decrease in pressure. This can be done either by physically moving the piston to change the volume, or by adding or removing weights from the piston to change the pressure. Either way, work is done to change the state of the system.
In cases like this where there is a change in either the pressure or volume of the system, specific work can be calculated using the formula:

Where:
- p = pressure of the fluid [Pa]
- v = specific volume of the fluid [m3/kg]
Notice that specific work is equal to the area under the curve of the pressure-volume diagram of the system. Hence, it is important to note that its value does not only depend on the initial and final states of the fluid, but also on the path used to change its state. For example, if the fluid took a linear path from State 1 to State 2, instead of a curved path, the amount of work done would be different.
Determining Specific Work for Different Types of Machines
Specific work can also be expressed in terms of mechanical work. The formula for work varies depending on the type of machine being used.
Specific Work of a Pump, Fan, or Turbine
For a pump, fan, or turbine working with an incompressible fluid, the formula for specific work can be written as:
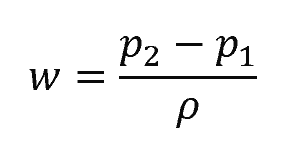
Where:
- p1 and p2 = initial and final pressure of the fluid [Pa]
- ρ = density of the fluid [kg/m3]
Compressor Specific Work
For a compressor working with a compressible fluid, such as air, specific work is normally derived from the initial and final specific enthalpies, assuming an adiabatic process:
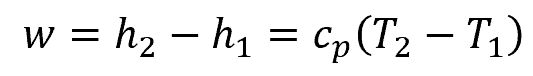
Where:
- h1 and h2 = initial and final specific enthalpies [J/kg]
- cp = specific heat of the fluid [J/kg-K]
- T1 and T2 = initial and final temperature [K]
In addition, the specific work of the compressor can also be expressed in terms of the compressor pressure ratio and efficiency:
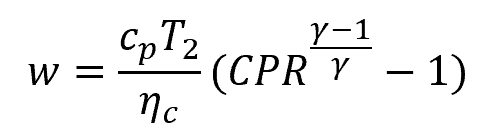
Where:
- ƞc = compressor efficiency [unitless]
- CPR = compressor pressure ratio [unitless]
- γ = specific heat ratio [unitless]
