The unique thermal properties of metals make them a valuable material in applications and industrial processes that require the use and manipulation of heat such as in manufacturing, construction, transportation, and energy production, among others. One of the crucial properties that affect their thermal behavior is specific heat.

Specific Heat Of Metals
The specific heat of a metal is the amount of heat required to raise the temperature of its unit mass by one degree. At the molecular level, it is a measure of the metal molecules’ ability to hold thermal energy.
This value is affected by various factors including the metal’s atomic structure, atomic weight, temperature, phase, and impurities, among others. Hence, different types of metal have different specific heat capacities.
Knowing this value is important in calculating the total amount of thermal energy needed to raise the temperature of a given mass of metal, as shown in the following equation:

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
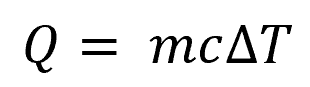
Where:
- Q = total amount of heat required [kJ or Btu]
- m = mass of metal [kg or lb]
- c = specific heat capacity [kJ/kg-K or Btu/lb-°F]
- ΔT = change in temperature [K or °F]
This is useful in applications that require the metal to be at a certain processing temperature, for example, in metal casting, welding, and heat treatment, where it is necessary to control temperature during the process in order to obtain the desired results.
Factors Affecting Specific Heat Of Metals
The specific heat differs from one metal to another. Even metals of the same elemental structure can have different values. In general, the specific heat value is affected by several factors including the metal’s atomic structure, mass, temperature, and the presence of impurities, among others.

Atomic Structure
The number and arrangement of atoms in the metal’s crystal lattice structure affect its ability to hold heat. The larger the number of atoms, the more tightly packed the atoms and the more closely they interact with each other. In general, metals with a more complex and compact structure tend to have a higher specific heat.
In addition, the metallic bonds between the metal atoms allow their outer electrons to be delocalized— that is, they can move freely throughout the crystal lattice. This allows the electrons to absorb energy in the form of heat. Hence, the greater the number of delocalized electrons, the higher the heat capacity.
Atomic Weight
According to the Dulong-Petit Law, due to the lattice vibrations in the solid, the specific heat of one mole of any solid element is constant and is estimated to be equal to 3R or approximately 25 J/mol-K, where R is the universal gas constant. Therefore, it follows that the specific heat of solid metals is directly proportional to the atomic weight.
Hence, metals with higher atomic weights would tend to have higher specific heat. This is because they have more particles that require more energy to be set in motion.

However, it is important to note that the Dulong–Petit Law is only an approximation and it has limitations. For example, it is not applicable for light atoms bonded strongly to each other, such as in metallic beryllium, even at room temperatures. It is also not applicable at very low (cryogenic) temperatures, where the quantum mechanical nature of energy predominates.
Temperature
Contrary to popular belief that the specific heat is constant, its value actually changes with respect to temperature. At higher temperatures, the particles are more likely to move and interact with each other as kinetic energy increases and bond vibration and rotation activate. This makes it more difficult to raise the temperature of the metal, resulting in higher specific heat.
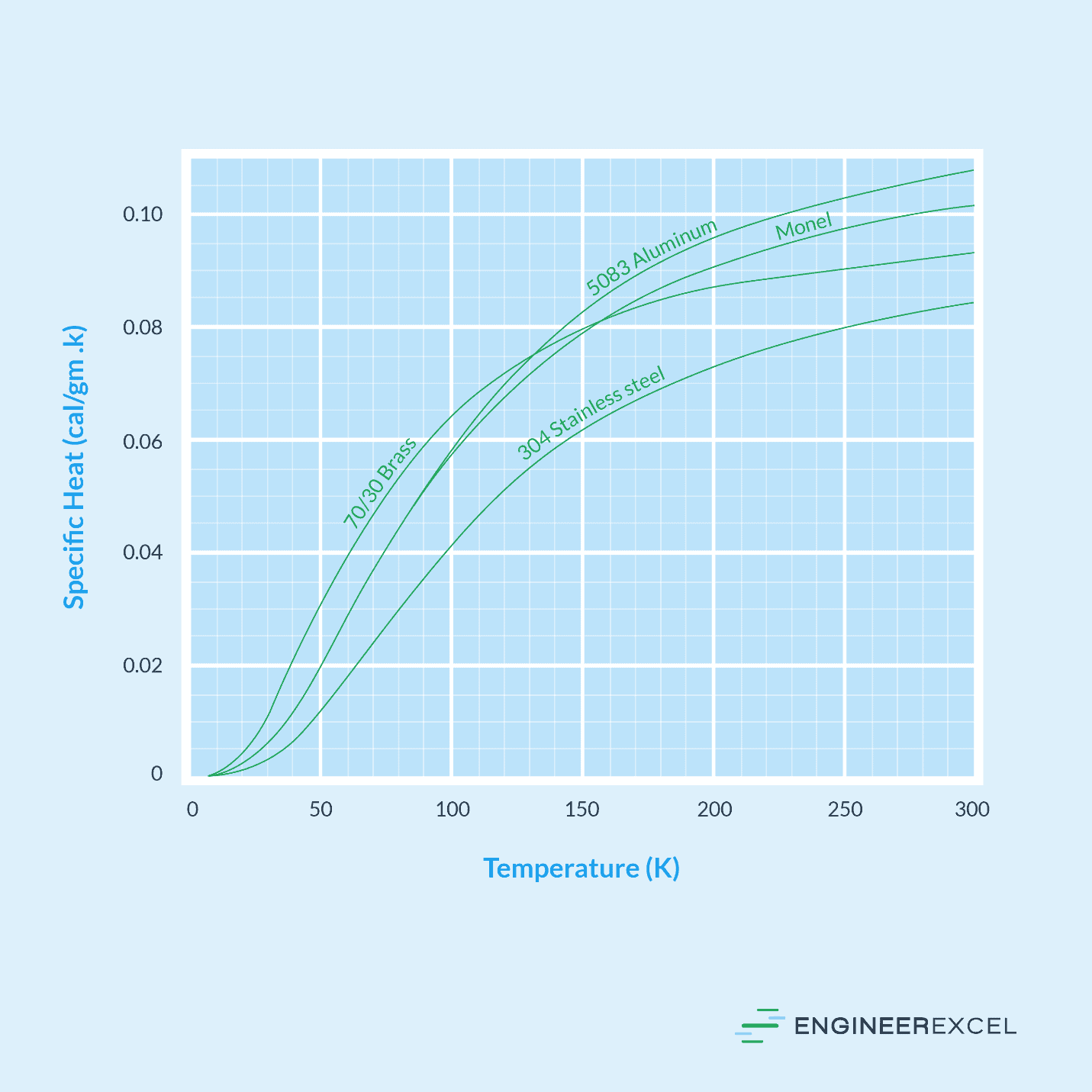
The graph below shows the behavior of the specific heat of brass, stainless steel, aluminum, and monel with respect to temperature.
Phase
When a metal undergoes a phase change, such as melting, its specific heat changes. Although the heat capacity of liquids has not been extensively studied due to the intricate nature of the liquid state, it is known that metals in their liquid state have a lower specific heat than in the solid state.
Impurities
The presence of impurities can interfere with the arrangement of the metal atoms in the crystal lattice. This can either increase or reduce its specific heat by a degree depending on the type and amount of impurities present. Ultimately, it makes it more difficult to predict the thermal behavior of the metal.
Specific Heat Of Common Metals
Metals generally have lower specific heat than other common substances like water, dry air, and concrete. Out of all the pure metals, lithium has the highest specific heat, which is equal to 3.559 kJ/kg-K or 0.850 Btu/lb-°F. On the other hand, there are a lot of pure metals that have very low specific heat values close to 0.126 kJ/kg-K or 0.030 Btu/lb-°F, such as bismuth, mercury, thorium, and thallium.
The specific heat values of some of the most common metals are listed in the table below.
Note that these values are assumed at room temperature. It is important to keep in mind that the specific heat changes with temperature and phase change.
Measuring Specific Heat Of Metals
Although there are published specific heat values for select metals, it may be necessary to measure the specific heat of a metal sample experimentally to get a more accurate result, especially since its value is affected by several other factors like impurities and temperature. There are several methods to do this, depending on the required accuracy and experimental conditions. The most common and simple methods are via calorimetry and electrical heating method.
Metal Calorimetry
Calorimetry involves heating a metal sample to a specific temperature and then quickly placing it into a well-insulated container of water or a calorimeter. The heat given off by the metal is absorbed by the water, causing the water temperature to rise and the metal temperature to drop to the same final temperature.
By equating the heat given off by the metal and the heat taken in by the water, the specific heat of the metal can be calculated using the formula:
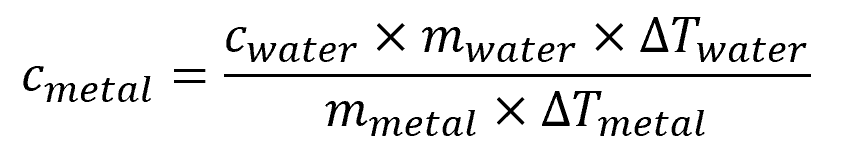
Where:
- cmetal = specific heat capacity of the metal [kJ/kg-K or Btu/lb-°F]
- mmetal = mass of the metal [kg or lb]
- ΔTmetal = change in temperature of the metal [K or °F]
- Cwater = specific heat capacity of water [kJ/kg-K or Btu/lb-°F]
- Mwater = mass of water [kg or lb]
- ΔTwater = change in temperature of water [K or °F]
Electrical Heating Method
The Electrical Heating Method uses a known amount of electrical energy to heat a metal sample. The specific heat of the metal can then be calculated using the equation:
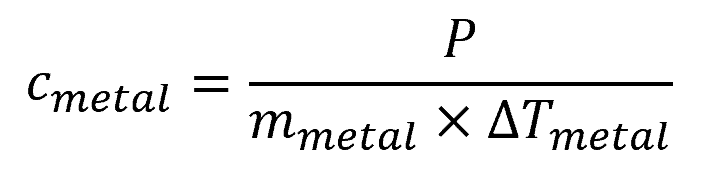
Where:
- P = electrical energy input [kJ or Btu]
These methods only apply to temperatures close to room conditions. At very high temperatures, more advanced techniques, such as Laser Flash Analysis, may be used.
