Point loads refer to external concentrated loads that act on a specific point within a body. It is typically represented as a single force vector with a specific magnitude and direction. In this article, we will delve into the mechanics of point loads, including some real-life examples, determining point load equivalents, and stress concentration due to point loads.
What is a Point Load
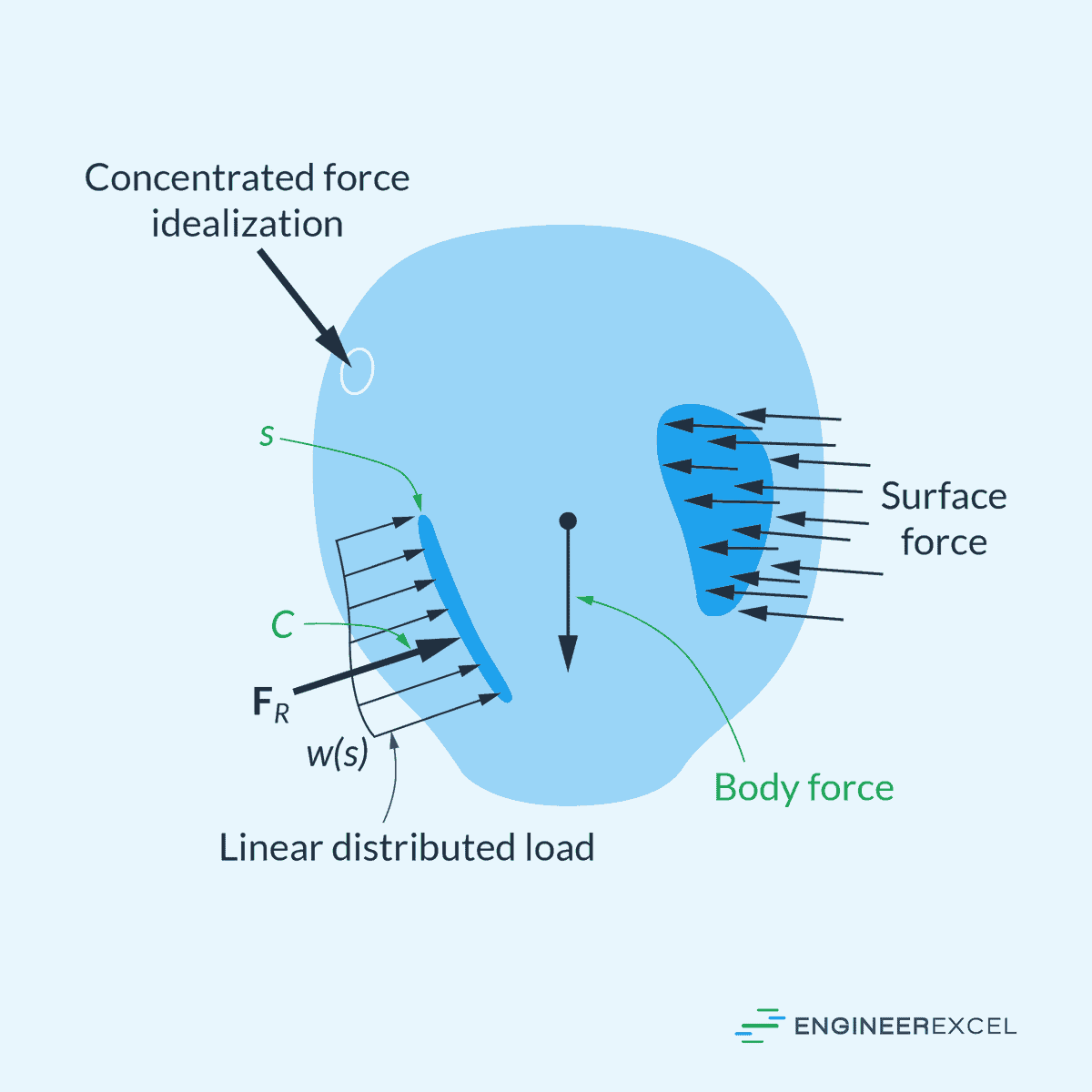
A point load refers to an external concentrated load that acts on a specific point within a body. It primarily occurs in two different forms, either as a body force or a surface force.

A body force develops when one body exerts force on another without any direct physical contact. For instance, the earth’s gravitational force and electromagnetic field create such effects.
While body forces affect each particle constituting the body, they can usually be represented by a single concentrated force, or a point load, acting on the body. In the case of gravitation, this force is referred to as the body’s weight and acts through its center of gravity.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
On the other hand, a surface force develops when there is direct contact between the surfaces of two bodies. In this case, the force is distributed over the contact area. When the contact area is small in comparison to the total surface area of the main body, the surface force can be idealized as a point load.
These are illustrated in the diagram below.
Point loads are the most basic type of loads in structural analysis and mechanics. This type of load is often represented as a vector with a specific magnitude and direction.
Real-Life Examples of Point Loads
In real-world applications, point loads can represent various scenarios. One common example is the pressure exerted on the support beams of a bridge when a vehicle passes over it. Since the vehicle is much smaller than the beam, its weight can be considered as a point load acting on the bridge structure.
Another example is a heavy piece of machinery or equipment placed on a floor. The weight of the machinery is concentrated at its base, leading to a point load on the floor beneath.
In mechanical engineering, the use of bearings can also be considered as a point load, where the weight or force acting on a rotating shaft is concentrated at specific points. Bearings are designed to handle point loads efficiently, allowing smooth rotation while supporting the weight and forces associated with the machinery.
Point Load Equivalent of a Distributed Loading
In many engineering applications, it is necessary to determine the point load equivalent of a distributed loading. This method simplifies the analysis of a structure subjected to distributed load by replacing the load with an equivalent single load, placed at a specific location.
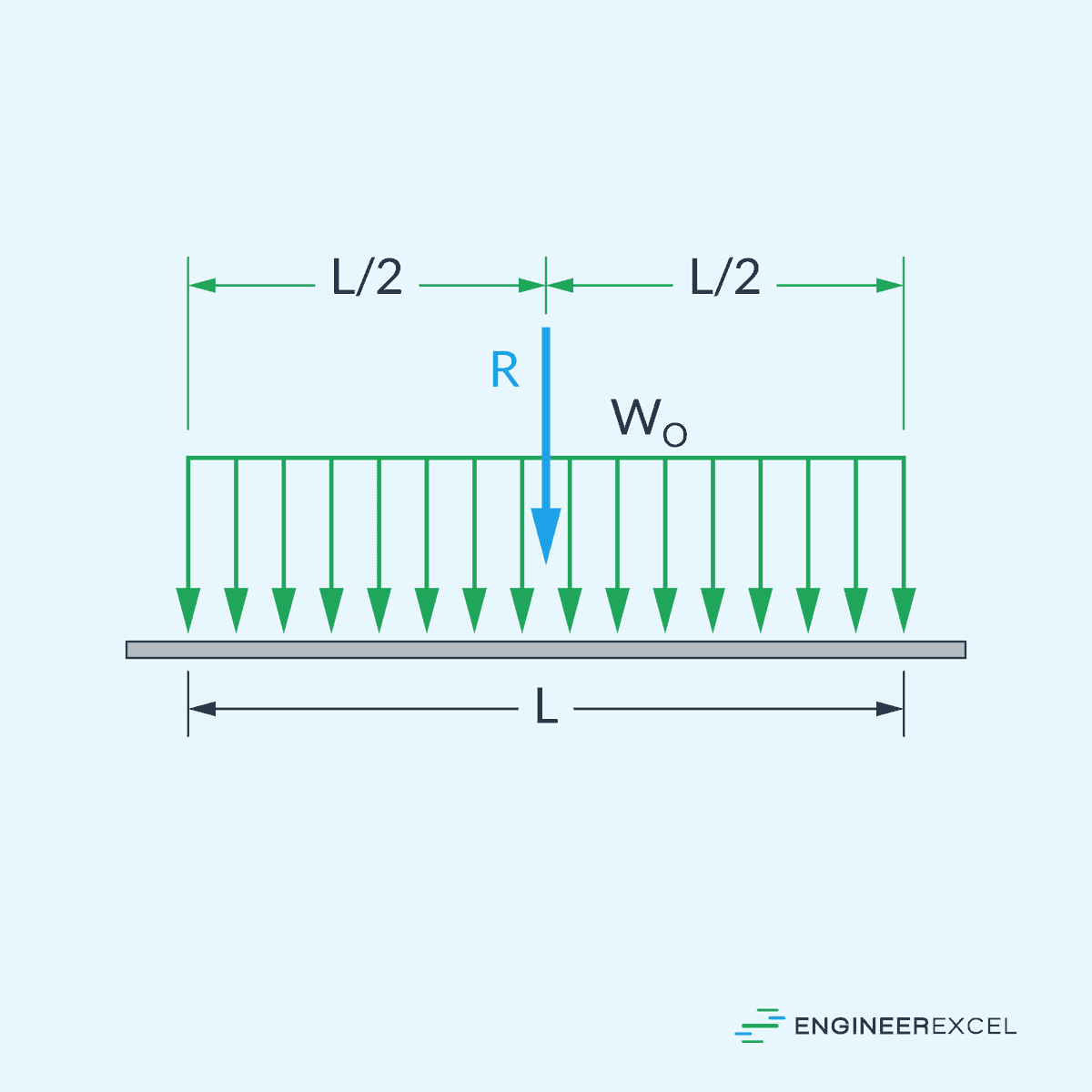
For instance, consider a beam subjected to a uniformly distributed load across its length. To calculate the point load equivalent, one must first determine the total load acting on the beam by integrating the distributed load’s intensity over the length. This total load can then be treated as a point load and applied at the centroid of the distributed load, which in the case of a uniform load, is at the middle of the span.
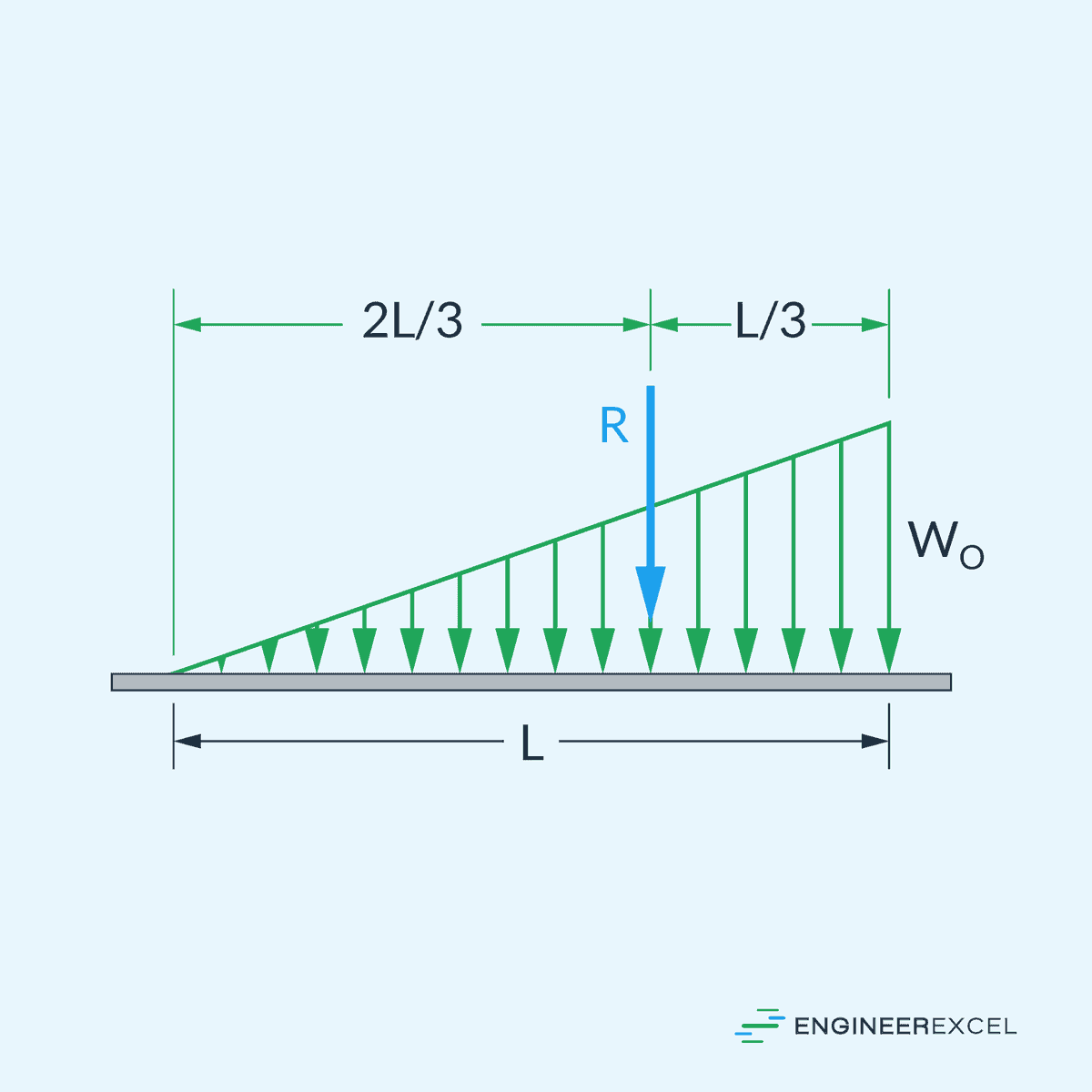
When dealing with a non-uniform or varying distributed load, the point load equivalent can still be found by integrating the load intensity over the length. However, the location of the equivalent point load will not necessarily be at the middle of the beam but at the centroid of the load’s area.
For instance, the point load equivalent of a triangular distributed loading is located at a distance equal to one-third of the length from the location of the maximum load, as shown in the diagram below.
It is important to use this method with caution, as it might not accurately reflect the actual stress distribution in some cases, especially when the contact area is not negligible compared to the body’s size.
Stress Concentration Due to Point Load
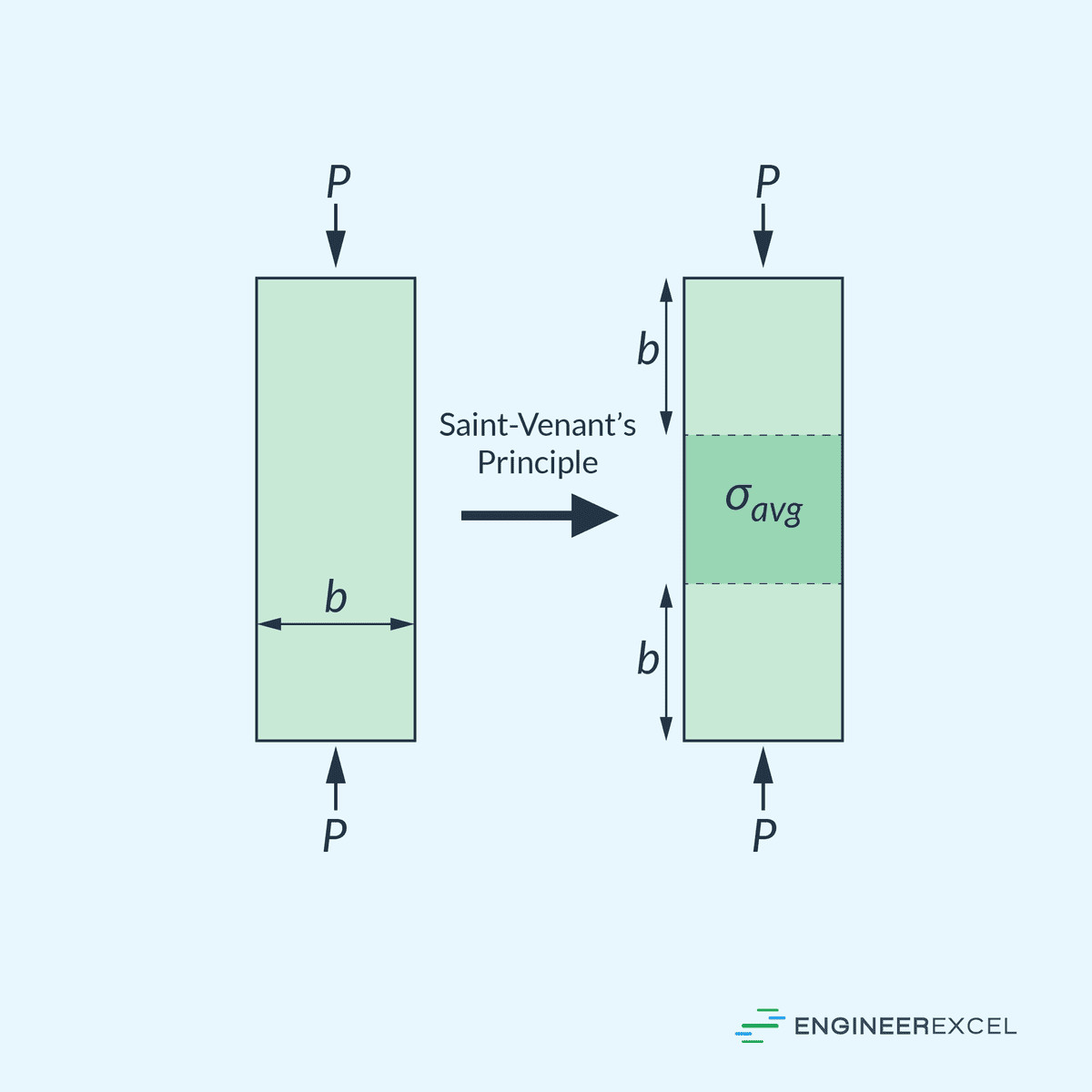
When a point load is applied to a structure, it creates localized stress at the point of application, as illustrated in the diagram below. This stress concentration can be significantly higher than the average stress experienced by the structure, resulting in complex deformations in the localized area.
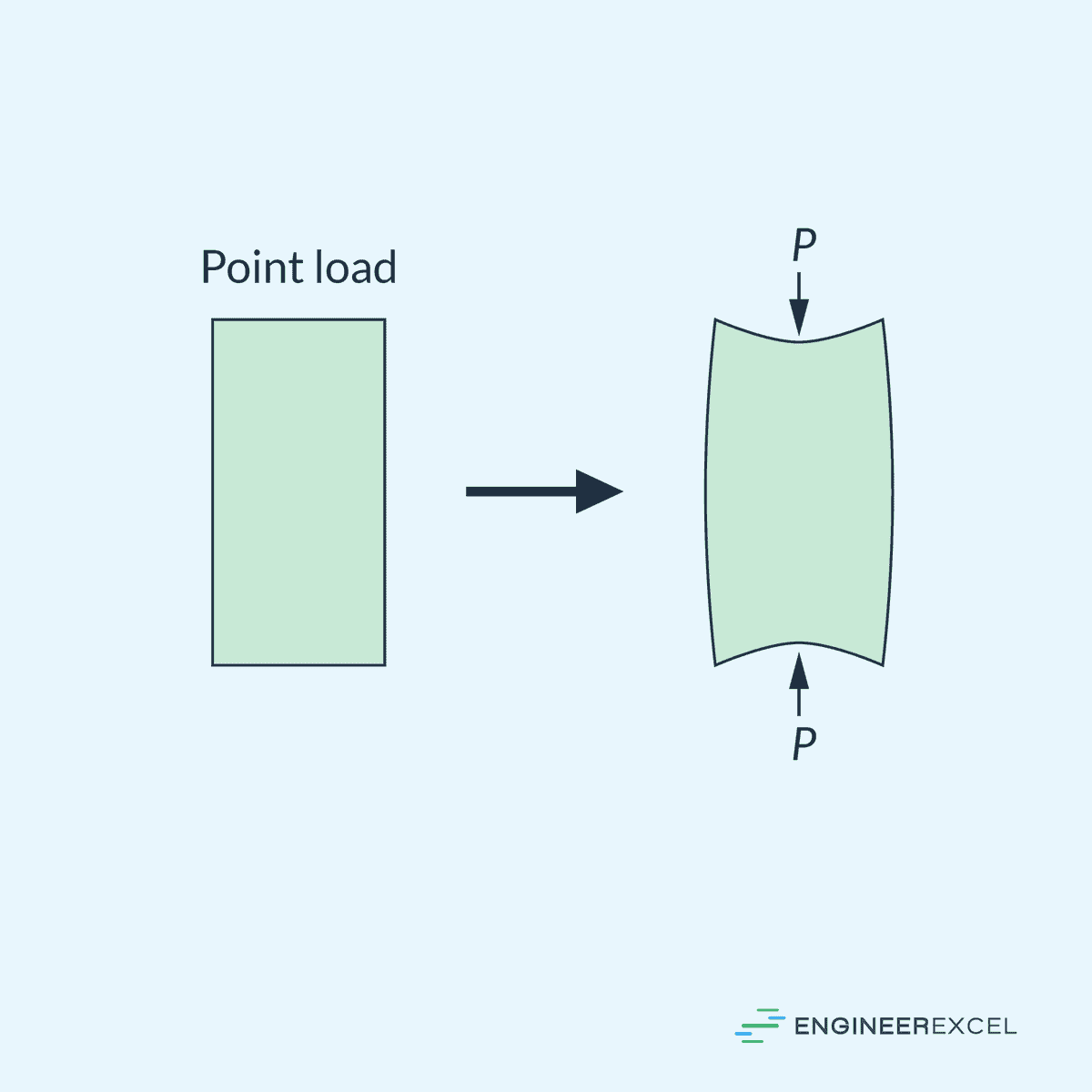
However, as you move farther away from the point load, the deformations start to become uniform. At a specific distance from the point load, the stress becomes evenly distributed, and the average stress approximation can be reliably used.
This distance is determined by the Saint-Venant Principle, which states that the average stress approximation is valid at a distance from the point load equal to the width of the structure. This is illustrated in the diagram below.