Modulus of elasticity is a measure of a material’s stiffness or resistance to deformation when subjected to stress. It quantifies how much a material will stretch or compress under a given force.

In this article, we will discuss the modulus of elasticity in detail, including its calculation, methods of measurement, factors affecting it, and the different types of elastic moduli.
What is Modulus of Elasticity
The modulus of elasticity, also known as Young’s modulus, is a fundamental property that quantifies the stiffness or rigidity of materials. Named after Thomas Young, who published an account of it in 1807, this property measures how much strain (deformation) a material undergoes in response to an applied stress. It is a key parameter in engineering and materials science, providing insight into the elastic behavior of a material under load.
This concept was first observed by Robert Hooke in 1676, who found that within the elastic region of a material, there is a proportionate increase in strain with an increase in stress. This relationship is famously known as Hooke’s law.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
When we represent this relationship graphically, the stress–strain diagrams for most engineering materials show a linear relationship within the elastic region, as shown below. The slope of this line, or the constant of proportionality up to the proportional limit, is what we refer to as the modulus of elasticity.
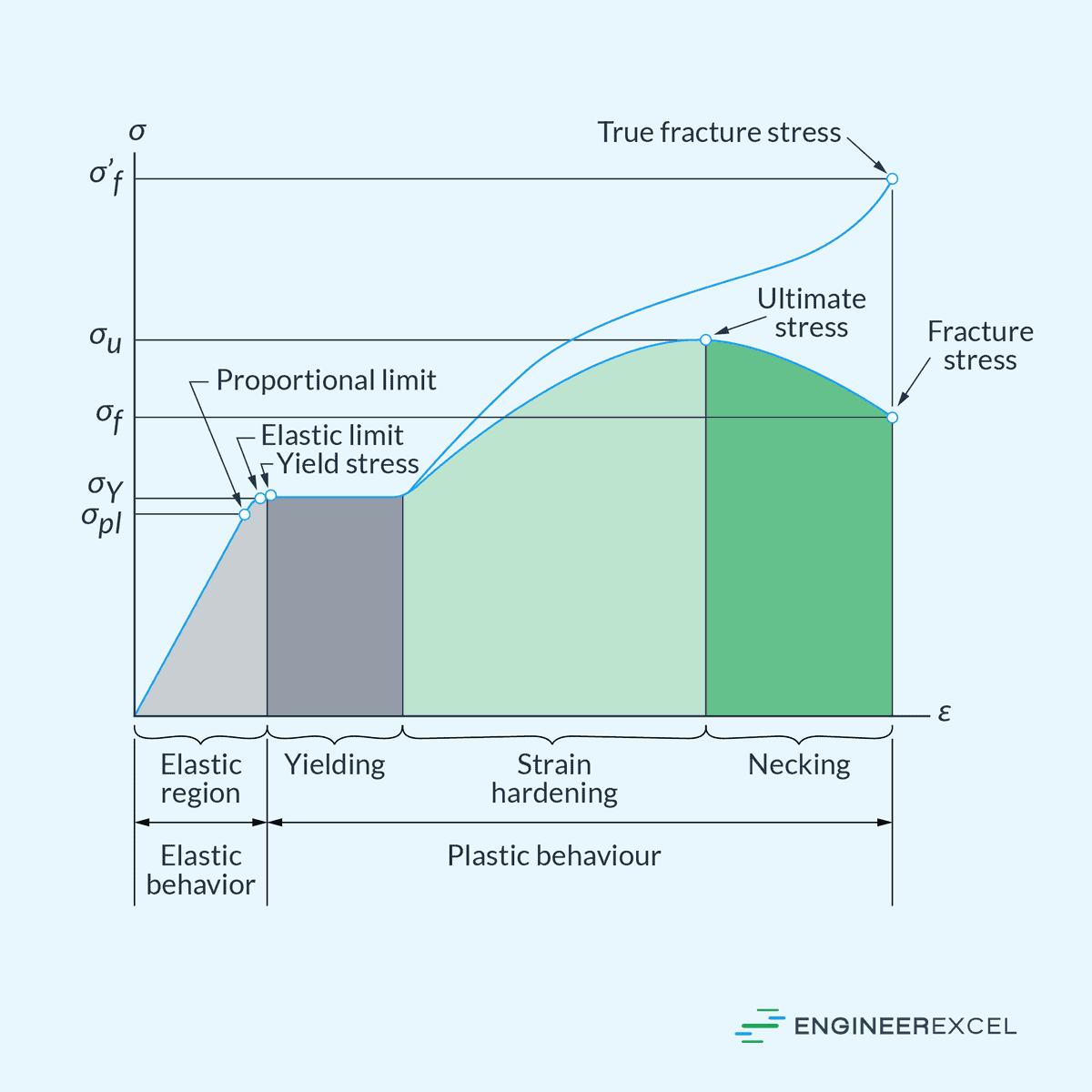
To understand the modulus of elasticity, it is important to know the concepts of stress and strain. Stress is the internal force per unit area that develops within a material as a result of an externally applied force. This is typically measured in units of pascals (Pa) or pounds per square inch (psi).
Strain, in contrast, is a dimensionless measure of deformation. It represents the relative displacement between particles within the material and is calculated by dividing the change in length by the original length of the material.
Elasticity denotes a material’s ability to resist a distorting influence and return to its original size and shape once that influence or force is removed. Materials with a high degree of elasticity are described as ‘elastic.’ The modulus of elasticity is an essential factor for predicting how much a material will deform under a given stress, which is vital for the design and analysis of structures and components.
Mathematically, the modulus of elasticity is defined as the ratio of stress to strain in the range where they are proportional to each other, in accordance with Hooke’s law:

Where:
- E = modulus of elasticity [Pa]
- σ = stress [Pa]
- ε = strain [unitless]
This linear relationship holds only up to the material’s elastic limit, beyond which permanent deformation occurs.
The modulus of elasticity is not uniform across all materials. For instance, steel has a high modulus of elasticity, indicating it is very stiff and does not deform much under load. Conversely, rubber has a much lower modulus of elasticity, which means it is more flexible and will experience greater deformation when subjected to the same stress level.
Measuring Modulus of Elasticity
Static Methods
One standard approach to measure the modulus of elasticity is through the construction of stress-strain curves from tensile or compressive tests. These experiments involve applying a slowly increasing load to a material sample and measuring the resulting deformations. The slope of the initial linear portion of the stress-strain curve is the modulus of elasticity for small strains, signifying the material’s elastic region where deformation is reversible.
Laboratories commonly use tensile test machines to apply known forces to a specimen, measuring the elongation with extensometers or strain gauges affixed to the sample.
Dynamic Methods
In dynamic testing, the modulus of elasticity can also be evaluated by observing the natural resonant frequencies of the material. When a material is vibrated, it oscillates at specific frequencies that are related to its stiffness. Analyzing these frequencies provides a means to calculate Young’s modulus without destroying the sample.
Vibration Testing Equipment is often used to excite the material and record its response. The equipment typically includes sensors that detect minute vibrations in the sample induced by an external actuator or impulse hammer.
Factors Affecting Modulus of Elasticity
The modulus of elasticity is influenced by a range of factors. These include the material’s composition, temperature conditions, and microstructural characteristics.
Material Composition
Materials are composed of atoms and molecules that interact through chemical bonds. The type and strength of these bonds directly influence the material’s modulus of elasticity.
Metals, for example, typically have a high modulus due to the strong metallic bonds between atoms. In contrast, polymers have a lower modulus because of their covalent bonding and the presence of van der Waals forces, which are weaker than metallic bonds.
Temperature Dependence
The modulus of elasticity is not a constant value; it varies with temperature. As the temperature increases, the amplitude of atomic vibrations grows, causing a decrease in the material’s modulus. This is due to the reduction in the stiffness of interatomic bonds at higher temperatures.
For instance, the performance of metals and ceramics at high temperatures is characteristically different from that at room temperature, often leading to a significant reduction in their modulus of elasticity.
Microstructural Factors
Microstructural elements such as grain size, presence of defects, and phase boundaries also affect the modulus of elasticity.
Finer grains can lead to higher modulus values as a result of the grain boundaries impeding dislocation motion. Defects such as vacancies, dislocations, and impurities can alter local atomic interactions and thus affect the material’s stiffness. Additionally, the distribution and type of phases within a material, influenced by the heat treatment history, can modify the overall elastic behavior of the material.
Types of Elastic Moduli
While Young’s modulus is the most commonly cited type of elastic modulus, there are actually several types, including Young’s modulus, Shear modulus, and Bulk modulus, each measuring the material’s response to different types of stress.
Young’s Modulus
Young’s modulus measures the stiffness of a material by describing its tensile elasticity. It is the ratio of tensile stress to tensile strain in the range of stress where Hooke’s Law applies. This modulus is important in predicting the extension of a material when exposed to a stretching force.
Shear Modulus
The Shear modulus, also known as the modulus of rigidity and denoted by G, defines how a material deforms under shear stress. It is the ratio of shear stress to the shear strain.
This modulus is essential for understanding the deformation that occurs when a force is applied parallel to one surface of a material while the opposite surface remains fixed. For instance, materials like aluminum exhibit a relatively high shear modulus, indicating greater resistance to shearing forces.
Bulk Modulus
Bulk modulus, symbolized as K, relates to the volumetric elasticity of a material. It quantifies the material’s compressibility when subjected to uniform pressure from all directions.
The reciprocal of the bulk modulus is compressibility. Essentially, it measures the material’s resistance to changes in volume. A high bulk modulus implies that the material is incompressible, like most metals, while a low modulus indicates higher compressibility, as seen in gases.
