The center of pressure is the point at which the total pressure force on a body immersed in a fluid can be considered to act. It varies with the shape and orientation of the body and can affect stability and control in aerodynamics and hydrodynamics.

In this article, we will explore the concept of the center of pressure, its calculation, and its practical applications in various engineering disciplines such as aircraft design, marine architecture, and automotive engineering.
What Is The Center Of Pressure
When an object is submerged in a fluid, it is subjected to fluid pressure distributed over its surface. If we neglect density changes in the fluid, then the pressure on the surface of the object varies linearly with depth, as shown in the diagram below.


Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
Assuming that the plane surface intersects the horizontal free surface at an angle θ and taking the line of intersection to be the x-axis, the pressure distribution can be mathematically expressed as:
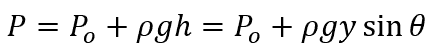
Where:
- P = absolute pressure at any point of the surface [Pa]
- Po = atmospheric pressure [Pa]
- ρ = density of the fluid [kg/m3]
- g = acceleration due to gravity [9.81 m/s2]
- h = vertical distance of the point from the free surface [m]
- y = distance of the point from the x-axis [m]
- θ = angle between the plane surface and the horizontal free surface [rad]
This pressure distribution can be transformed into a resultant hydrostatic force by integrating the pressure distribution over the entire surface area as follows:
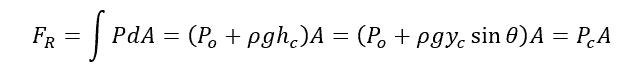
Where:
- FR = resultant force due to fluid pressure [N]
- A = total surface area [m2]
- hc = vertical distance between the centroid of the surface and the free surface [m]
- yc = distance between the centroid of the surface and the x-axis [m]
- Pc = pressure at the centroid of the surface [Pa]
The center of pressure is the point where this resultant force can be considered to act. In other words, it is the point on the surface where, if you could sum up all the pressure forces acting on it, the resultant force would act through that point. It is essentially the equivalent point for the pressure forces as the center of mass is for the gravitational forces.
As shown in the diagram above, the center of pressure does not necessarily pass through the centroid of the surface. Instead, it acts below it toward the high-pressure side. This phenomenon can be explained by considering the distribution of pressure within a fluid.
Pressure increases with depth in a fluid due to the weight of the overlying fluid. As a result, the pressure acting on the submerged surface is higher at greater depths. This non-uniform pressure distribution results in a net force that is not necessarily aligned with the centroid of the surface but rather acts in a direction that counteracts the pressure distribution.
Calculation Of Center Of Pressure
Suppose the center of pressure is located at coordinates (xp, yp). The x and y locations of the center of pressure can be determined by equating the moment of the resultant force to the moment of the distributed pressure force about the y-axis and the x-axis, respectively. This results to the following set of formulas:
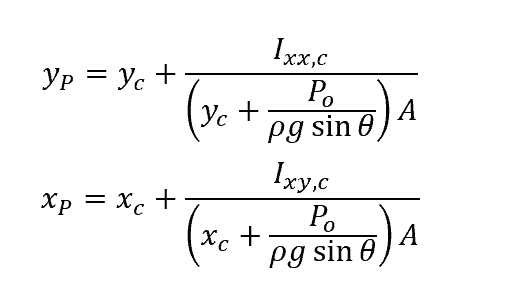
Where:
- yp = distance of the center of pressure from the x-axis [m]
- xp = distance of the center of pressure from the y-axis [m]
- Ixx,c = second moment of area about the x-axis passing through the centroid of the area [m4]
- Ixy,c = second moment of area about the y-axis passing through the centroid of the area [m4]
If we ignore the atmospheric pressure, the formulas above can be simplified as follows:
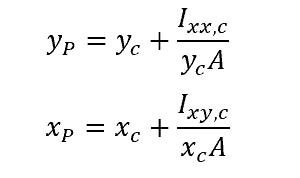
The formula for calculating the second moment of area for some common shapes are shown below. For symmetrical shapes, the second moment of inertia about the y-axis is zero, hence, xp=xc. In this case, the center of pressure lies directly below the centroid on the y-axis.

Once yp is known, the vertical distance of the center of pressure from the free surface can be calculated as follows:
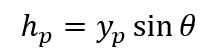
Where:
- hp = vertical distance of the center of pressure from the free surface [m]
Practical Applications
The center of pressure is a fundamental concept in fluid mechanics with significant applications across various engineering disciplines.
Aircraft Design
In aircraft design, the center of pressure plays a critical role in stability and control. Engineers calculate the center of pressure of a wing or airfoil to ensure that it is correctly positioned relative to the aircraft’s center of gravity.

This alignment is essential for maintaining the aircraft’s stability during flight, as imbalances can lead to pitch, roll, or yaw motions.
Marine Architecture
For marine architecture, the center of pressure is vital in the design of ship hulls and underwater vehicles. It impacts their hydrodynamic performance, influencing stability, rolling, and pitching motions.
Naval architects place great emphasis on the center of pressure to ensure that a vessel’s buoyancy effectively counteracts the weight distribution, which affects handling characteristics and seaworthiness.
Automotive Engineering
In automotive engineering, understanding the center of pressure influences vehicle aerodynamics. Specifically, it helps in the design of aerodynamic elements such as spoilers, diffusers, and body shape. These adjustments aim to minimize aerodynamic drag and maximize downforce, which improves tire traction and vehicle handling characteristics at high speeds.
