An object that is submerged in a fluid, either a liquid or gas, will be subject to a buoyant force. This force will act on the part of the object that is submerged, and can be used to determine how the object will respond. Calculating this buoyant force is the first step in evaluating the response of the object.
Understanding How To Calculate Buoyant Force
The buoyant force is the force that a fluid exerts on a floating object. According to Newton’s Third Law, when a system containing a fluid and a floating object, the fluid is exerting a force equal and opposite to the force of gravity that is pulling the object downward, as shown in the following figure:
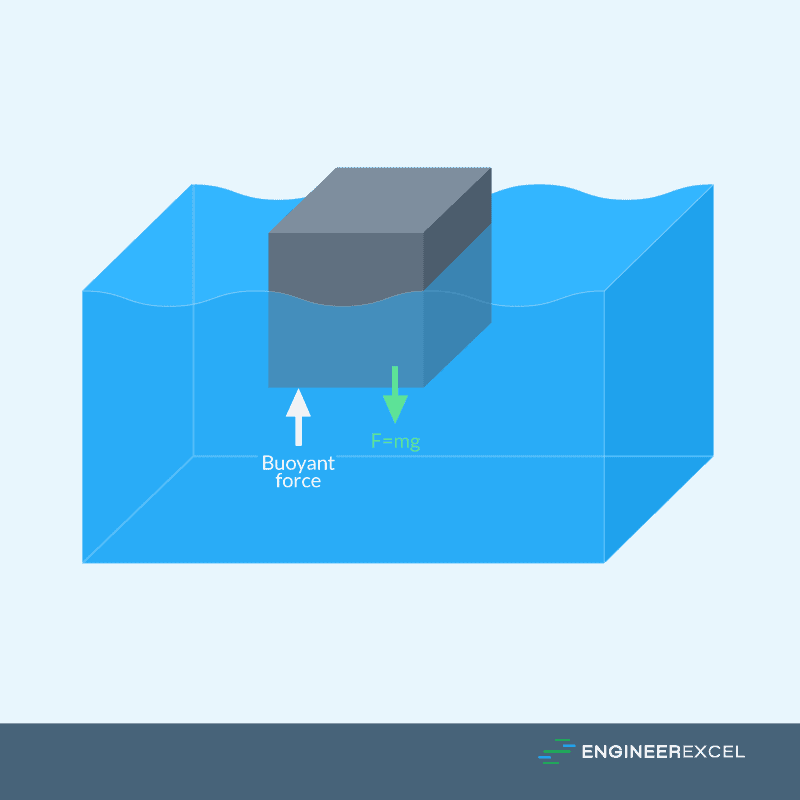
Determining Buoyant Force On An Object
To calculate the buoyant force acting on an object, the following equation is used:

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
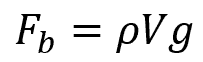
where:
- Fb is the buoyant force, with units of N
- ρ is the density of the fluid the object is floating in, with units of kg/m3
- V is the volume of the submerged part of the object, with units of m3
- g is the gravitational acceleration, with units of m/s2
To use the above equation and calculate the buoyant force on an object, there are a series of steps to be carried out, as introduced in the following.
Determine The Volume
The first step is to determine the volume of the submerged part of the object. This is because the buoyant force only acts on the part that is exposed to the fluid, as shown in the following figure:
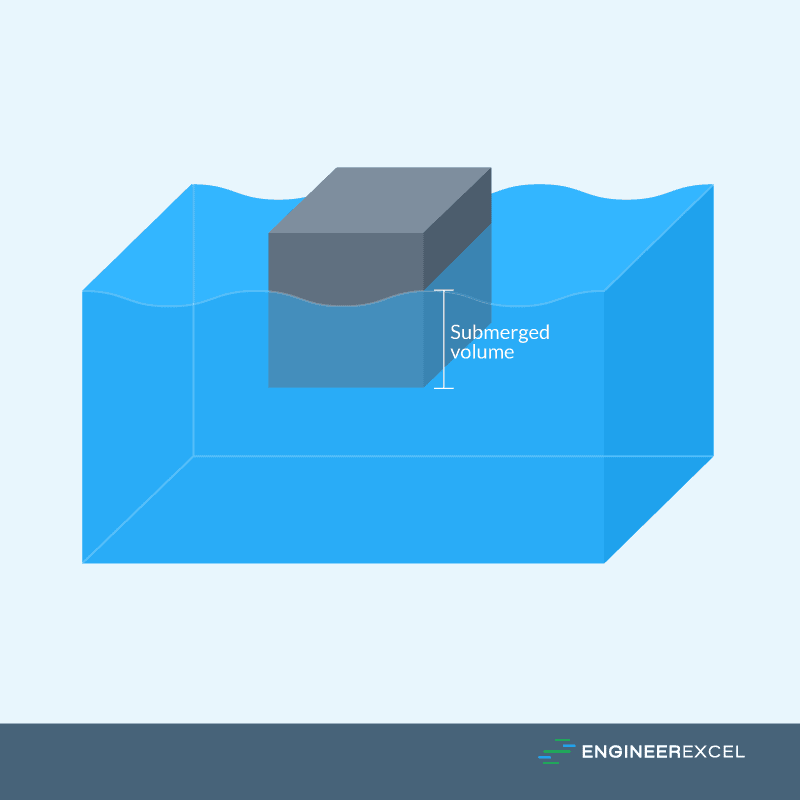
As more of an object is submerged in the fluid, the buoyant force will increase. An object may be completely submerged in a fluid but still float, a state called neutral buoyancy. An example of the use of neutral buoyancy is the Neutral Buoyancy Lab, where astronauts get as close to the microgravity environment of space as they can on Earth in what is essentially a giant swimming pool.
In some instances, it is possible to calculate the submerged volume by taking measurements of the length, width, and height of the submerged portion and multiplying them together. However, in most cases, such as that of irregular shaped objects, these three measurements are not available.
As an alternative, the volume of fluid that is displaced can be used. There exist various methods for determining the volume of fluid displaced by an object, any of which can be used, and the process will not be discussed here.
Determine The Fluid Density
The second step is to find the density ρ of the fluid in which the object is floating. If the fluid is known, such as water, the density may be found in a lookup table. For fluids for which the density is not known or readily available, the density may be calculated by taking a sample and using the following equation:
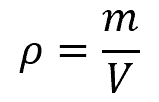
where m is the mass of a sample of the fluid, with units of kg. Then, the density will be the mass divided by the volume of a sample, giving units of kg/m3.
Apply The Equation
Using the submerged volume of the object and the density of the fluid, and using the gravitational constant at the Earth’s surface of 9.81 m/s2, the buoyant force can be calculated. If the system is not near the Earth’s surface or is not at Earth, the actual gravity will need to be calculated for use in the equation.
Example Calculation
As an example, assume that 10 m3 of an object is submerged in seawater, which has a density of 1026 kg/m3. The buoyant force exerted by the seawater on the object is calculated as follows:
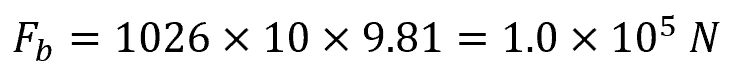
Applying The Buoyant Force
The most common practical application of the buoyant force is determining whether the force exerted by a fluid will be enough to offset the weight of an object, such as a boat. As discussed originally, for the system to be static, the buoyant force will be equal and opposite to the weight of an object. If the buoyant force is less than the object weight, the object will sink. If the buoyant force is more than the weight, the object will rise to the surface.
Buoyant Force Less Than Object Weight
For a case where the buoyant force is less than the weight of the object, the weight of the object will overcome the buoyant force and sink. An example of this scenario would be a rock dropped into a lake.
Example Calculation
As an example, assume that an object with a weight of 1177 N and volume of 0.05 m3 is dropped into fresh water, which has a density of 1000 kg/m3. Will this object sink or float? To answer this, calculate the buoyant force and compare it to the weight, as follows:

Since Fb < 1177 N, the weight of the object will overcome the buoyant force, and the object will sink.
Buoyant Force More Than Object Weight
If the buoyant force acting on a completely submerged object is more than the object weight, the object will rise to the surface of the fluid. An example of this would be a balloon held under water and then released, as shown in the following figure:

Example Calculation
As an example, assume an object with a weight of 50 N and a volume of 2.5 m3 is released under water. To determine whether the object will rise to the surface, the buoyant force is calculated and compared to the weight of the object:

Since Fb > 50 N, the buoyant force will overcome the weight of the object, and the object will rise to the surface.
Points To Consider
Remember that the buoyant force is applicable to an object that is submerged in a fluid. As a fluid can be either a liquid or a gas, there is a buoyant force caused by air. This is the force that causes a helium-filled balloon to rise. In that case, the weight of the balloon (and helium) is less than the force the air itself exerts. This is shown in the following:
The density of air is 1.225 kg/m3. The density of helium is 0.1785 kg/m3. Assume a balloon that weighs 0.1 N when empty is filled to a volume of 1.5 m3 with helium (the thickness of the balloon can be neglected). In this case, the total weight of the helium-filled balloon will be:
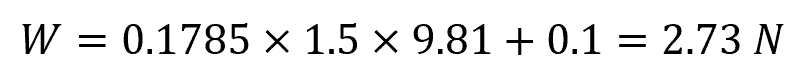
Then, the buoyant force acting on the balloon will be:
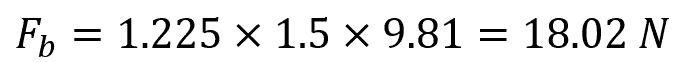
If the same balloon were filled with air, its weight would be 18.02 N, which is more than the buoyant force, so the balloon will fall.
