Hydrostatic pressure refers to the pressure exerted by a fluid at rest due to the force of gravity acting upon it. This pressure increases with depth in a fluid, as the weight of the fluid above adds to the pressure at any given point.

In this article, we will explore the principles of hydrostatic pressure and its applications in fluid mechanics.
Fundamentals of Hydrostatic Pressure
Hydrostatic pressure refers to the pressure at a given point within a static fluid. For a fluid at rest, the only stress present is the normal stress due to pressure; there are no shear stresses because there is no relative motion between fluid layers. Hence, pressure in a static fluid varies solely because of the fluid’s weight and the effects of gravitational acceleration.
In hydrostatics, the pressure exerted by a static fluid on a surface is perpendicular to that surface at all points. This pressure arises due to the weight of the fluid above the point of measurement and increases linearly with depth, as shown by the formula:

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
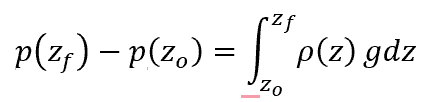
Where:
- p = hydrostatic pressure [Pa]
- zo = height of the zero-reference point of pressure [m]
- zf = height of the point of measurement [m]
- ρ = density of the fluid [kg/m3]
- g = acceleration due to gravity [9.81 m/s2]
Because many liquids can be considered incompressible, a reasonably good estimation can be made by assuming a constant density throughout the liquid. This simplifies the hydrostatic pressure equation to:
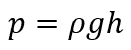
Where:
- h = height of the liquid column above the point of measurement [m]
To give an example, consider a point submerged in a liquid, as shown in the diagram below.
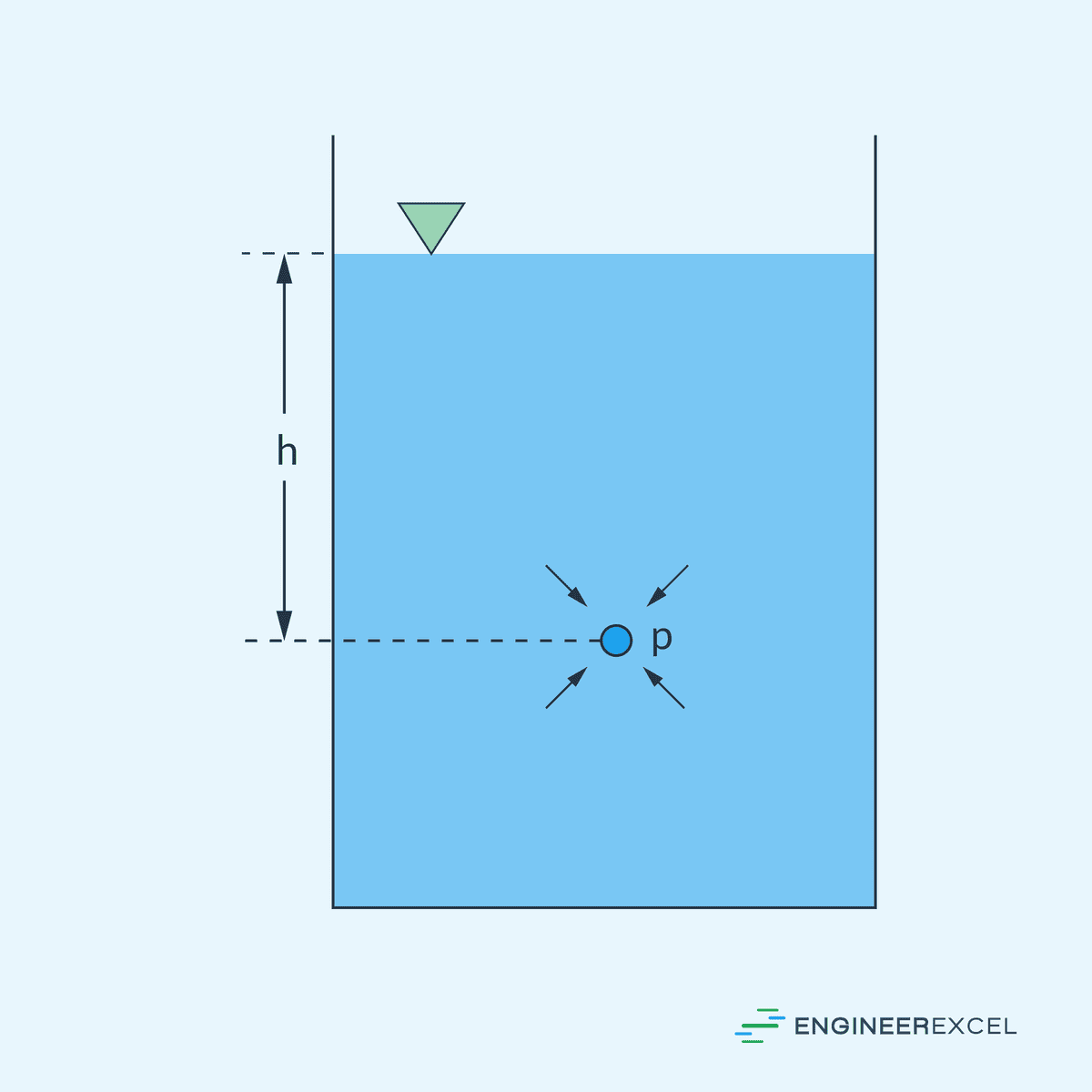
To calculate the absolute pressure at point p, we would have to obtain the sum of the atmospheric pressure at the surface and the hydrostatic pressure due to the weight of the liquid column above the point:
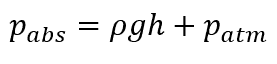
Where:
- pabs = absolute pressure [Pa]
- patm = atmospheric pressure [101,325 Pa]
The principles governing hydrostatic pressure dictate that it does not depend on the total volume of the fluid or the shape of the container. Unlike aerostatic pressure, which refers to the pressure within a static gas and can change with volume and temperature, hydrostatic pressure remains unaffected by these factors due to the incompressibility of liquids.
The relationship between hydrostatic pressure and depth is important when designing structures that must withstand fluid pressure, such as dams or submarine hulls.
Applications Of Hydrostatic Pressure
Hydrostatic pressure is an integral concept in fluid mechanics that plays an important role in calculating forces on submerged surfaces and has far-reaching impacts on modern infrastructure and technology.
Fluids In Tanks And Vessels
Hydraulic systems depend on the principles of hydrostatic pressure to function correctly. For instance, the pressure at any point within a fluid-containing vessel is essential for the design of tanks and vessels. Designers ensure that the walls can withstand the pressure exerted at various depths, especially in large storage tanks where the bottom experiences the highest pressure due to the weight of the fluid above.
Buoyancy And Floatation
The concept of buoyant force is a direct outcome of hydrostatic pressure. This force allows for calculating the floatation capabilities of ships and underwater vehicles. Engineers must consider the distribution of hydrostatic pressure around the hull to ensure stability and buoyancy, critical factors in the marine industry for safety and operability.
Water Pressure Distribution In Dams
The distribution of hydrostatic pressure against a dam is pivotal for its design and safety. As water pressure increases with depth, engineers must calculate the force exerted at different levels to construct safe and stable dam walls. The understanding of pressure distribution permits the assessment of necessary wall thickness and reinforcement to avoid structural failures.
Measuring Hydrostatic Pressure
Manometers
Manometers are devices that utilize a column of fluid to measure pressure difference. The basic principle is that the pressure exerted by the fluid column is directly proportional to the height of the fluid, which is affected by the pressure difference across the manometer. Types of manometers include the simple U-tube manometer, which is often filled with mercury, and the inclined-tube manometer, which provides increased accuracy for small pressure differences.
Piezometers
A piezometer is a type of manometer used for measuring liquefied pressure within a system. It consists of a tube inserted vertically into the fluid and the pressure is indicated by the height to which the fluid rises in the tube. The key limitation of piezometers is that they are only effective for measuring positive pressure in fluids at rest and cannot measure below atmospheric pressure.
Pressure Transducers
Pressure transducers convert pressure into an electrical signal and are used for more diverse and dynamic measurements. They can be designed to measure a wide range of pressures and provide quick and accurate data. Calibration against known pressures is necessary to ensure the accuracy of pressure transducers.
Hydrostatic Paradox
The Hydrostatic Paradox refers to the counterintuitive phenomenon in fluid mechanics where the force exerted by a fluid on the bottom of a container is independent of the container shape. Despite varying container geometries, the force at the base solely depends on the fluid height and the area of the container’s bottom.
Consider three containers of different shapes but with identical base areas. When these containers are filled to the same height with a liquid, they exert identical hydrostatic pressure on their bases. This outcome might appear paradoxical because the total volume, and consequently the weight of the fluid, differs among the containers. However, the explanation lies within the foundational principles of hydrostatic pressure, which state that pressure at a point in a fluid at rest is the same in all directions.
Hydrostatics In Multi-Layered Fluid Systems
In multi-layered fluid systems, hydrostatic pressure distribution is affected by the density and thickness of each layer. Assuming a system with n distinct, immiscible layers, the pressure at any given depth can be calculated using the principle of hydrostatic equilibrium. It maintains that the pressure at the bottom of a layer is the pressure at the top of the layer plus the weight of the fluid column above it.
The formula for the pressure at the interface between two successive layers is given by:
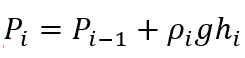
Where:
- Pi = pressure at the bottom of the ith layer [Pa]
- Pi-1 = pressure at the top of the ith layer [Pa]
- ρi = density of the ith layer [kg/m3]
- hi = height of the ith layer [m]
