Evaluating Derivatives of Equations in Excel with VBA

We can extend the concept of finite differences into VBA if we know the function and aren’t constrained to dealing with tabular data. For example, let’s assume that the equation below defines the position of an object:

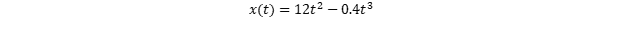
We can calculate the velocity using finite differences in VBA. Open the VBA editor with Alt-F11. Right-click the worksheet in the project window and choose Insert > Module. Create a function called Position with one argument, t:

Function Position(t)

Then define Position according to the equation above:

Position = 12 * t ^ 2 – 0.4 * t ^ 3

Elevate Your Engineering With Excel

Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.

Find Out More

That’s all there is to the position function. Create the velocity function, also with one argument, t:

Function Velocity (t)

In this function, we’ll calculate the derivative of position using the central difference method. First, we’ll set the spacing, h, to a very small value:

h = 0.0001

Now, we can use the central difference equation to calculate the velocity:

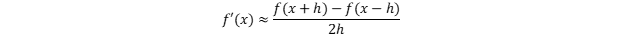
In VBA form this will be:

Velocity = (Position(t + h) - Position(t - h)) / (2 * h)

With both functions complete, your code should be:

Function Position(t)
Position = 12 * t ^ 2 – 0.4 * t ^ 3
End Function

and

Function Velocity (t)
h = 0.0001
Velocity = (Position(t + h) - Position(t - h)) / (2 * h)
End Function

Return to the worksheet so you can use these functions. In the first cell of the Position column, enter the formula:

    =Position(B11)

Likewise, in the velocity column, enter:

=Velocity(B11)

Select both of these cells and double-click the fill handle to fill them down. Select all three columns of data and insert a scatter chart.

To make it easier to read, put the velocity on a secondary axis. Right-click the velocity data and choose Format Data Series, then click Plot Series on Secondary Axis in the task pane that opens. Click the y-axis, with the task pane still open, and change the Minimum bound to 0. This is the resulting chart:

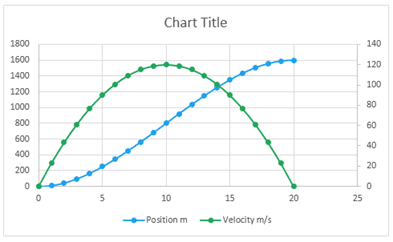
Of course, we always want to check if the result makes sense. When the velocity is zero, the position is zero. When the velocity reaches its peak, the position is increasing most rapidly. Finally, when velocity goes back to zero, the position also stops increasing. So yes, it appears to make sense.

This example demonstrates that finite differences are a simple way to calculate the derivative of a function in VBA with good accuracy provided the time step is sufficiently small.