As heat is applied to water (or any other liquid), the water will transition to steam. This vapor will exert pressure, and the point at which the pressure exerted by the water vapor is the same as the ambient pressure is called the boiling point. Therefore, with different ambient environments, the vapor pressure will be different, which will have an impact on the boiling of water.

Water Vapor Pressure
The vapor pressure of water is the pressure at which the water will transition from a liquid to a gas (vapor). Specifically, the vapor pressure is point at which the water is in a state of equilibrium, with the same number of water molecules transitioning from liquid to gas and from gas to liquid. The following image shows the two states of water in equilibrium:
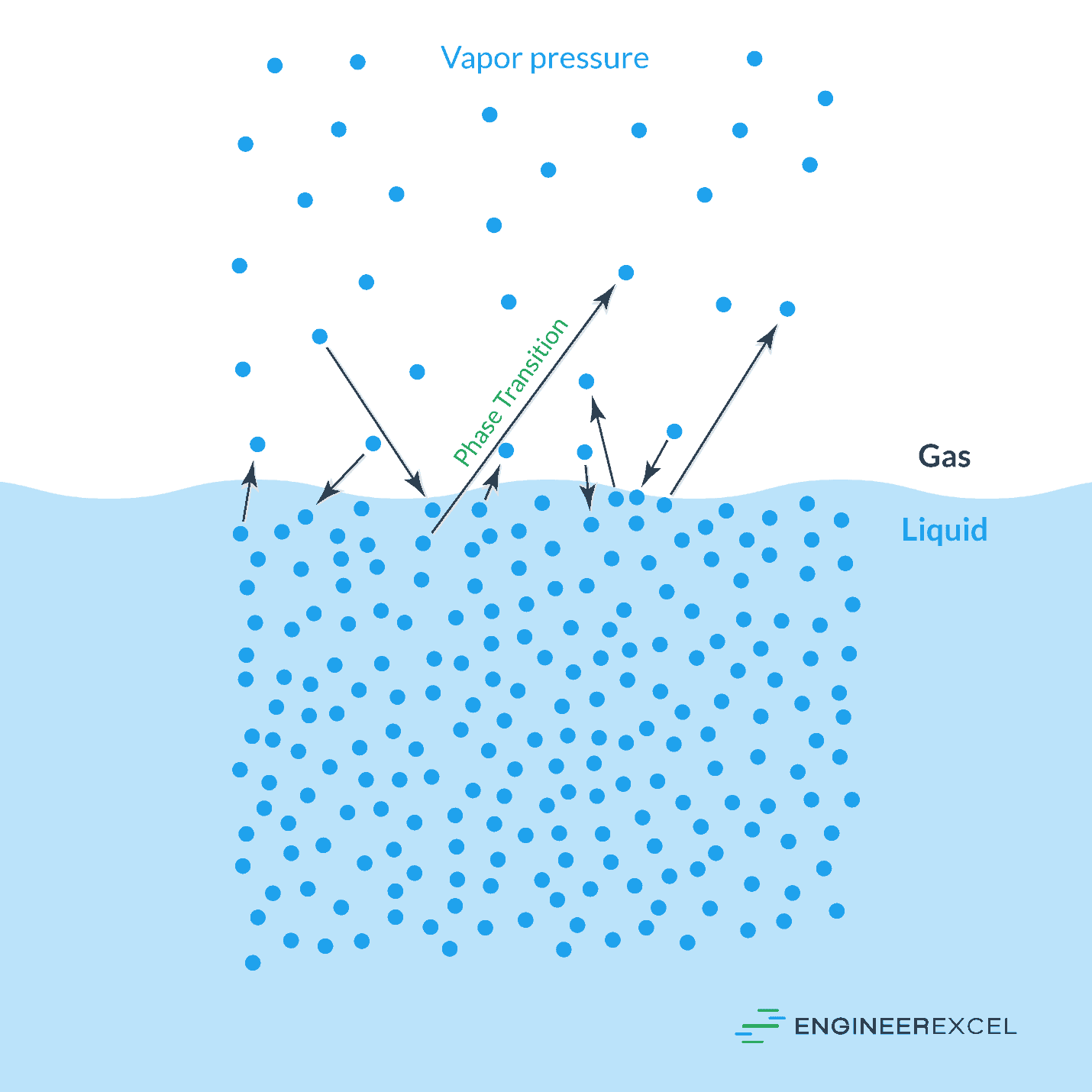
The Effect Of Temperature
Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
In general terms, as heat is applied to water (or any other liquid), the intermolecular bonds will break down and the liquid will transition into a vapor form (steam). As the temperature increases, the rate of this transition will speed up. However, once the water reaches its vapor pressure, additional heat will no longer increase the rate of transition from liquid to steam.
Determining Vapor Pressure
The vapor pressure of water may also be referred to as the saturation pressure. Often, a lookup table or a chart like the one below will be used to find the vapor pressure of a liquid.
Using the above chart, the relationship between the pressure and temperature can be seen. Therefore, for a given temperature, the associated vapor pressure can be found. However, to accurately calculate the vapor pressure at a given temperature, the Clausius-Clapeyron equation can be used.
Clausius-Clapeyron Equation
The Clausius-Clapeyron equation is as follows:
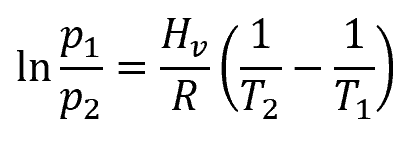
where:
- p1 is the vapor pressure at temperature T1, with SI units of atm
- p2 is the vapor pressure at temperature T2, with SI units of atm
- Hv is the enthalpy of vaporization, with SI units of kJ/mol and is equal to 40.7 kJ/mol
- T1 is the starting temperature, with SI units of K
- T2 is the final temperature, with SI units of K
- R is the ideal gas constant, with SI units of J/mol∙K and is equal to 8.314 J/mol∙K
The Clausius-Clapeyron equation will need to be rearranged appropriately to solve for the vapor pressure.
Example Calculation
For water, the vapor pressure at sea level (ambient pressure of 1 atm) is reached at a temperature of 212°F (373 K). In a scenario with a temperature of 175°F (353 K), determining the vapor pressure equal to the ambient pressure is as follows:
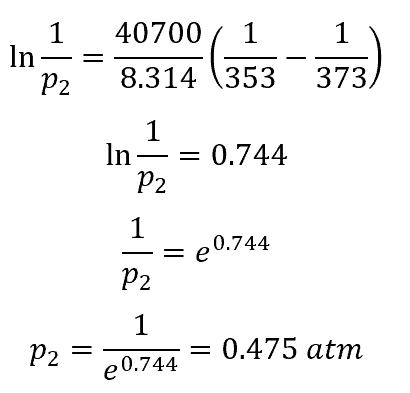
Increasing Temperature
Once the water being heated has reached the vapor pressure, additional heating will no longer be possible. At sea level, the vapor pressure (boiling point) of water is 212°F. This is the highest temperature that liquid water at sea level can reach. Even if the water were being heated by a heat source at 500°F, the liquid water would remain at 212°F.
To get the liquid water to a temperature higher than 212°F, it is necessary to increase the vapor pressure, i.e., increase the ambient pressure. This is the concept behind a pressure vessel, which can be used to maintain water in a liquid state at a high temperature.

Alternatively, at lower pressures, the boiling point of water will decrease. For example, the boiling point of water at an altitude of 10,000 ft is 193°F.
Applying The Vapor Pressure Of Water
To transport high-temperature water in a liquid state to power a turbine, the water will need to be at a pressure higher than ambient as it moves through the pipe. If that high-pressure pipe were to break, the liquid water at a high temperature would rapidly vaporize upon exposure to a lower ambient pressure.
Impurities
This discussion of water vapor pressure is only applicable to pure water. In most practical applications, water is not pure, and will often contain traces of other chemicals. These other chemicals, liquid or otherwise, will impact the vapor pressure of the water. Water with impurities will often times have a lower vapor pressure. To determine how impurities affect the water vapor pressure, Raoult’s Law can be applied:
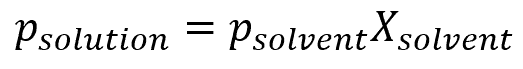
where:
- psolution is the vapor pressure of the solution, with units of lb/ft2
- psolvent is the vapor pressure of the solvent, in this case water, with units of lb/ft2
- Xsolvent is the molar fraction of the solvent, which is a dimensionless value
Determining the molar fraction of the solvent is a process that involves understanding the makeup of the overall solution, including the composition of the solute (impurities). For reference on this process, refer to this website.
