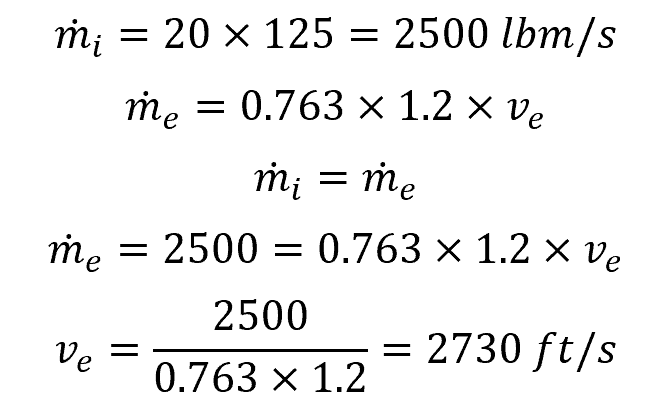The mass flow rate is an important engineering parameter in fluid dynamics, which includes the flow of liquids and gases. When calculating the mass flow rate, understanding the specific scenario and what needs to be determined will help in setting up the equations.

Calculating The Mass Flow Rate
In fluid mechanics, the mass flow rate is the amount of mass that passes a given point in a given amount of time. There are different ways to calculate the mass flow rate, depending on the overall situation and what information is known.
Typically, the mass flow rate is calculated as a function of the volumetric flow rate or a function of the system area and fluid velocity. In certain applications, pressure differences can be used in evaluating the mass flow rate.
Using The Volumetric Flow Rate

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
The volumetric flow rate is a measure of the volume of fluid passing a given point. Using the volumetric flow rate, the mass flow rate can be calculated as follows:
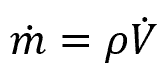
where:
- ṁ is the mass flow rate, with units of lbm/s
- ρ is the density of the fluid, with units of lbm/ft3
- V̇ is the volumetric flow rate, with units of ft3/s
Example Calculation
To demonstrate calculating the mass flow rate using the volumetric flow rate, assume a scenario where a fluid of density 0.035 lbm/ft3 flows through a pipe with a volumetric flow rate of 50 ft3/s. In this example, the mass flow rate is:
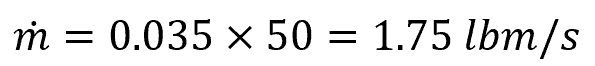
Using The Area And Velocity
The mass flow rate can also be calculated using the area through which the fluid flows and the velocity at which it flows, as follows:
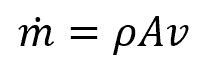
where:
- A is the area, with units of ft2
- v is the velocity, with units of ft/s
Example Calculation
To calculate the mass flow rate using the area and velocity, assume a scenario where a fluid of density 62.71 lbm/ft3 flows through a pipe with an area of 0.05 ft2 at a velocity of 21 ft/s. The mass flow rate is:

It should be noted that the volumetric flow rate is equal to the area times the velocity. This can be useful when applying the conservation of mass to a fluid flow calculation.
Using Pressure Differences
In some engineering scenarios where there is a pressure difference, such as flow through a pipe with a varying cross-sectional area, the mass flow rate can be calculated using that difference. Such a scenario is shown in the following figure:
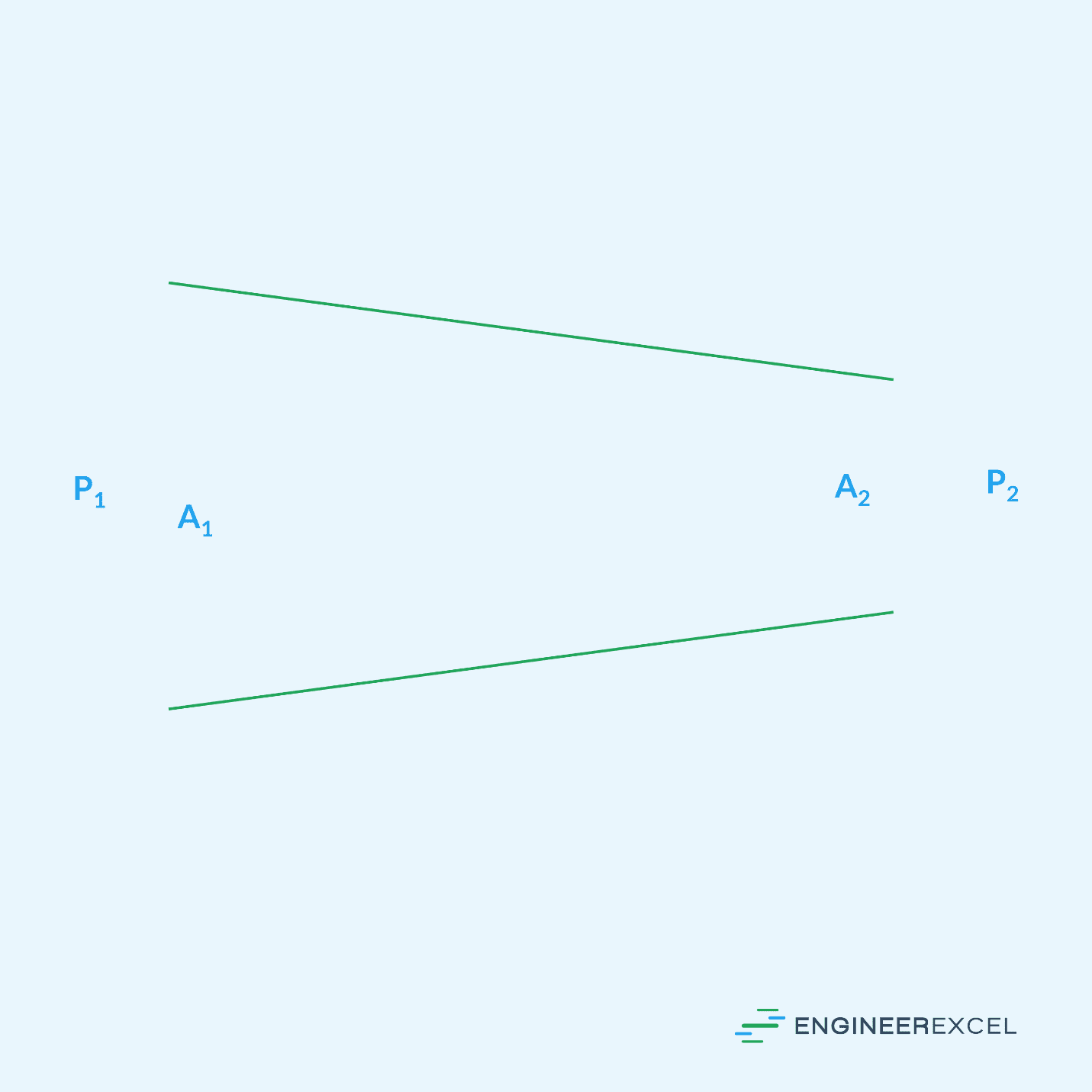
In such a scenario, Bernouli’s equation can be used to determine the flow rate from the pressure difference. To calculate the mass flow rate in a pipe with a changing cross-section using the pressure difference, the following equation is used:
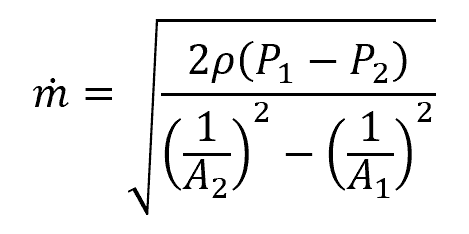
where:
- A1 is the inlet cross-sectional area, with units of ft2
- A2 is the outlet cross-sectional area, with units of ft2
- P1 is the inlet pressure, with units of lbf/ft2
- P2 is the outlet pressure, with units of lbf/ft2
- ρ is the density in kg/m3
Example Calculation
The mass flow rate of a fluid with density 800 kg/m3 through a pipe with an inlet area of 2 m2, an outlet area of 1 m2, an inlet pressure of 40 Pa, and an outlet pressure of 25 Pa can be calculated as follows:
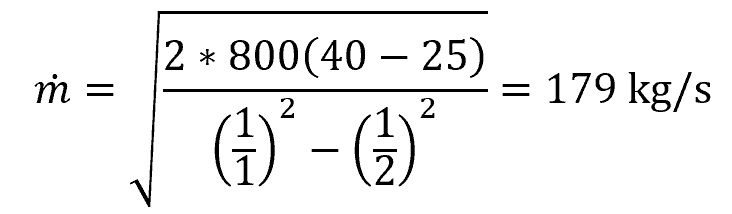
Mass Flow Rate And Conservation Of Mass
In most practical engineering applications, mass will be conserved. That is, the mass exiting a system will be equal to the mass entering the system. When evaluating the mass flow rate, this fundamental property of physics plays an important role.

When calculating the mass flow rate at a specific point in a fluid flow, the fact that the mass in the system will not change can be used for further calculations, such as in the Bernoulli equation to calculate the lift on an aircraft wing. Another example is the flow of gases through a rocket nozzle, which is then used in the calculation of the rocket’s thrust.
Example Calculation
An example of applying the conservation of mass to the mass flow rate involves the flow of exhaust gases from a rocket engine. At the nozzle entrance, the exhaust gases are flowing at a volumetric flow rate of 125 ft3/s at a density of 20 lbm/ft3. The gases exit the nozzle, which has an area of 1.2 ft2, into the atmosphere, which has a density of 0.763 lbm/ft3. Using the conservation of mass and the mass flow rate, the exhaust velocity can be calculated as follows: