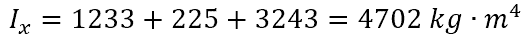The parallel axis theorem can be used to calculate the area moment of inertia about any axis. This theorem equates the moment of inertia about the central axis to an arbitrary axis.
Derivation of the Parallel Axis Theorem
In general, the moment of inertia of an arbitrary shape about the x-axis can be calculated as follows:
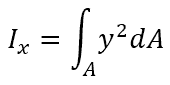
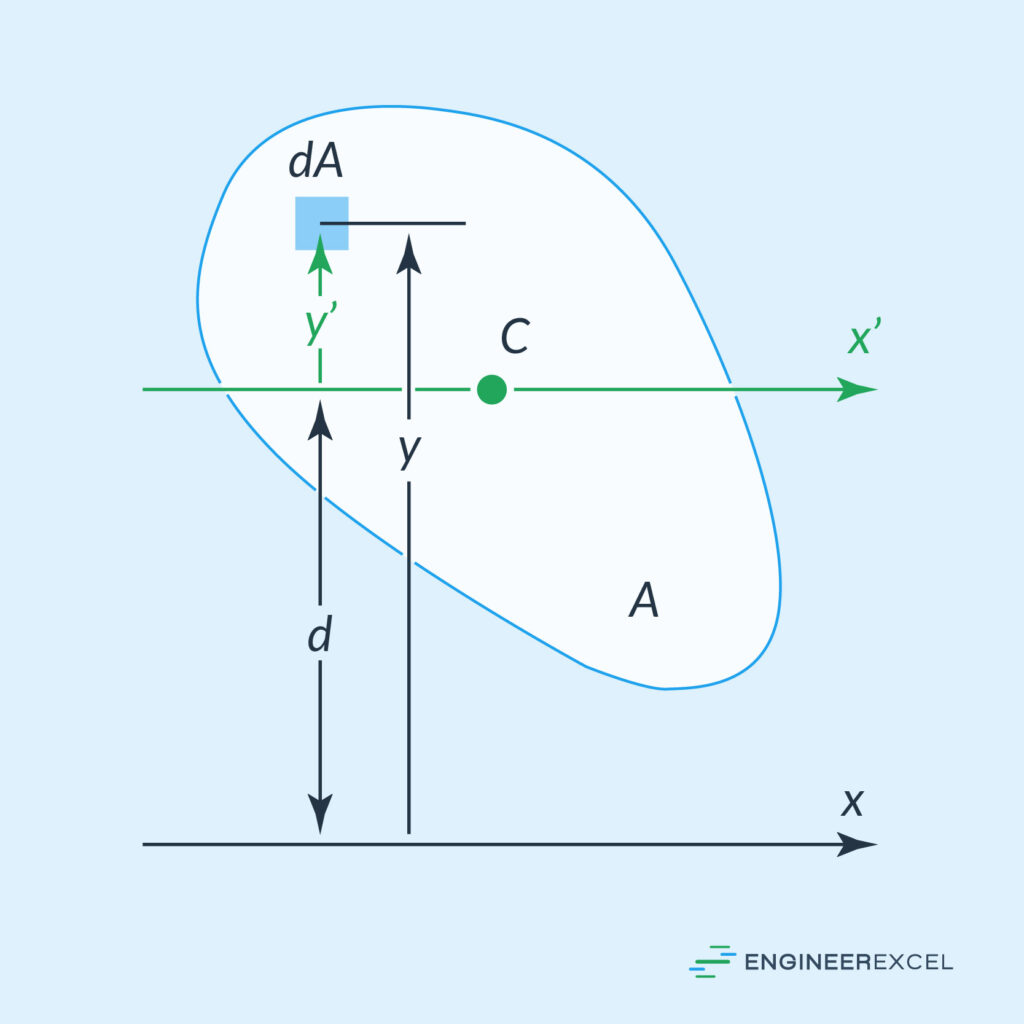
For the shape shown in the figure below, the x’-axis parallel to the x-axis passes through the centroid C of the shape. The distance between the two axes is d. Dividing the area of the shape A into differential elements dA, the distance from the x-axis to an element is y and the distance from the x’-axis is y’.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
Through the parallel axis theorem, the moment of inertia of the shape can be equated as follows:

The relationship between y and y’ is:

Substituting:

The first equation is the first centroidal moment of inertia of Ix’. The third equation is the total area of the shape A. The second equation is the first moment of area about the x’-axis:
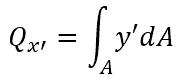
Therefore,
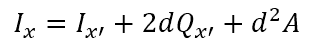
Because the x’-axis passes through the centroid of the body, Qx’ is equal to 0. Therefore,
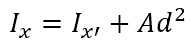
The above equation can be generalized to any axis. Therefore, the moment of inertia of an arbitrary shape about any axis can be determined by adding Ad2 to the parallel centroidal moment of inertia.
Applying the Parallel Axis Theorem
The parallel axis theorem is useful when an object’s cross-section is a composite of several common cross-sections.
Moment of Inertia of Common Shapes
The moment of inertia about any axis can be easily determined for common shapes using a look-up table or other reference. A body with a complex shape can be divided into multiple common shapes, and the moments of inertia of these shapes can be combined using the parallel axis theorem. Images of common shapes and their moments of inertia are shown below:
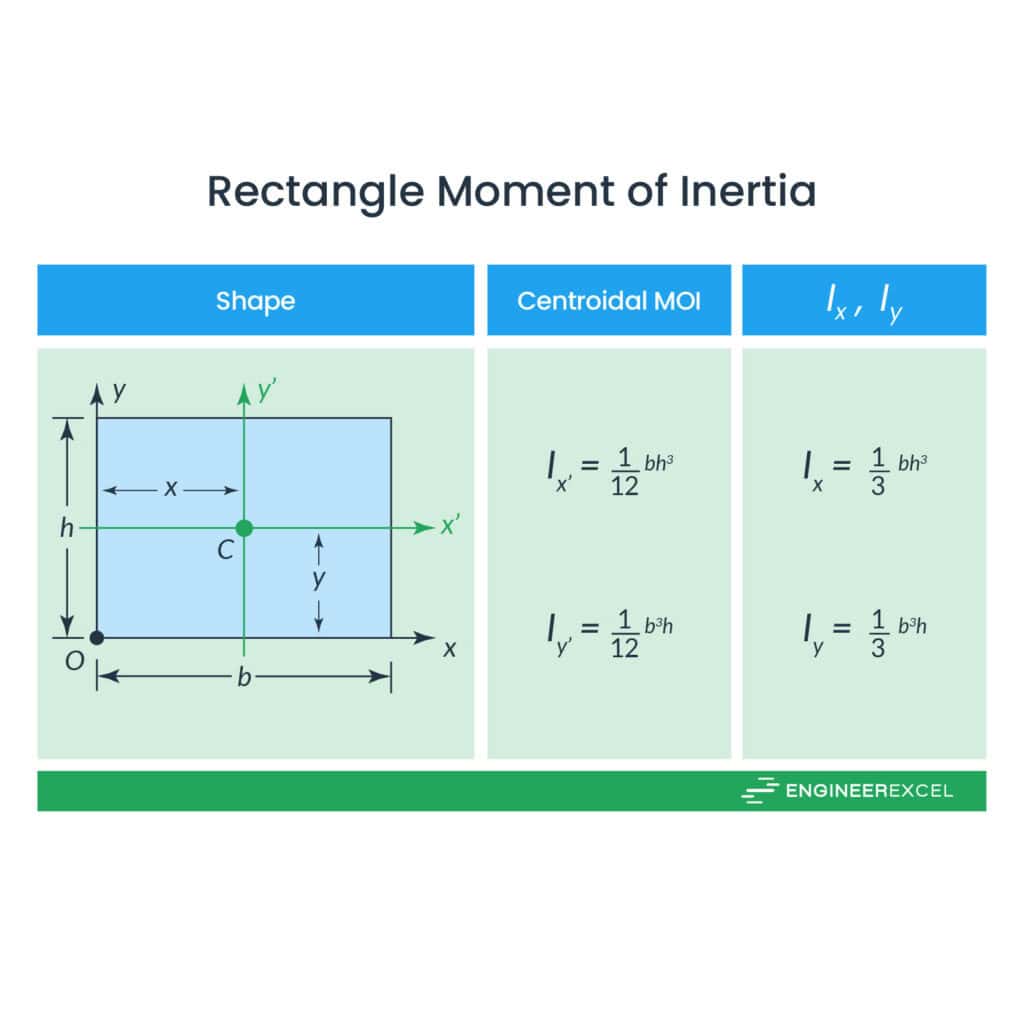
Rectangle Moment of Inertia
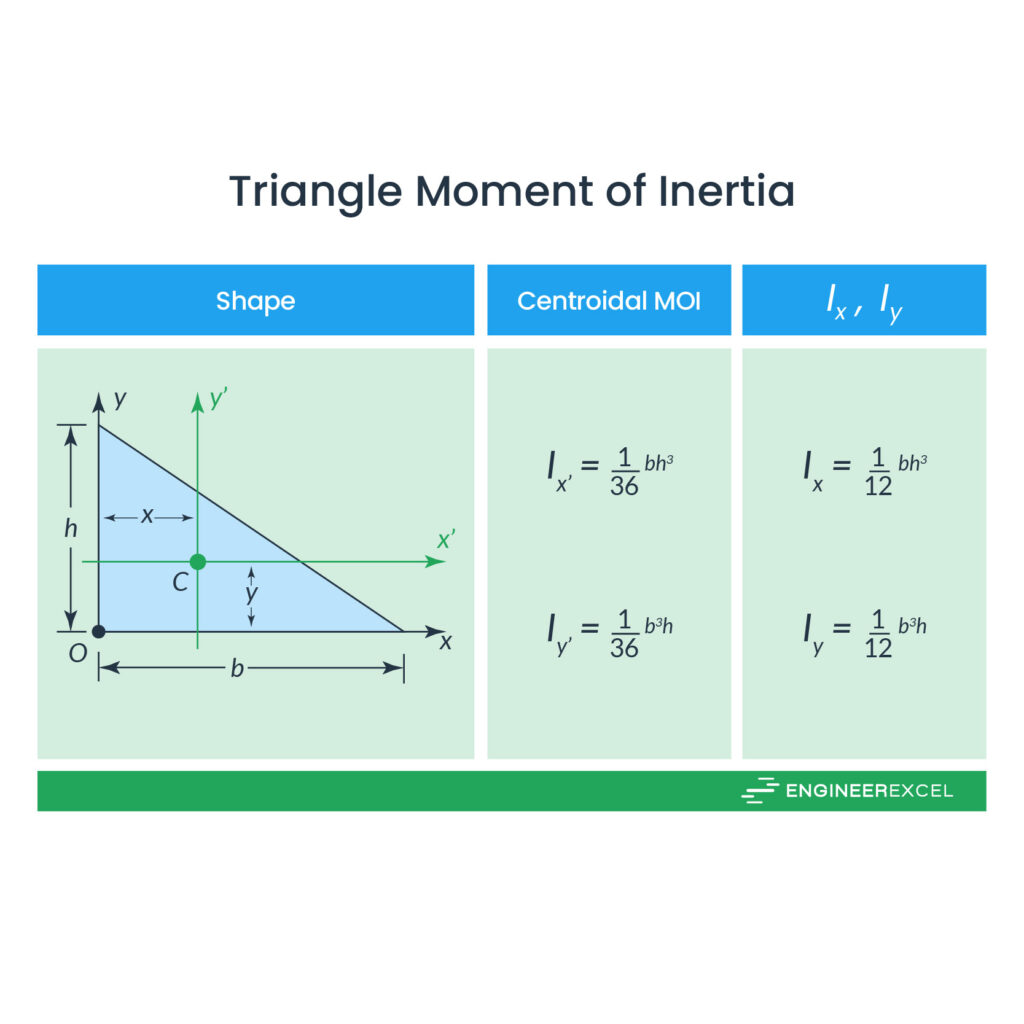
Triangle Moment of Inertia
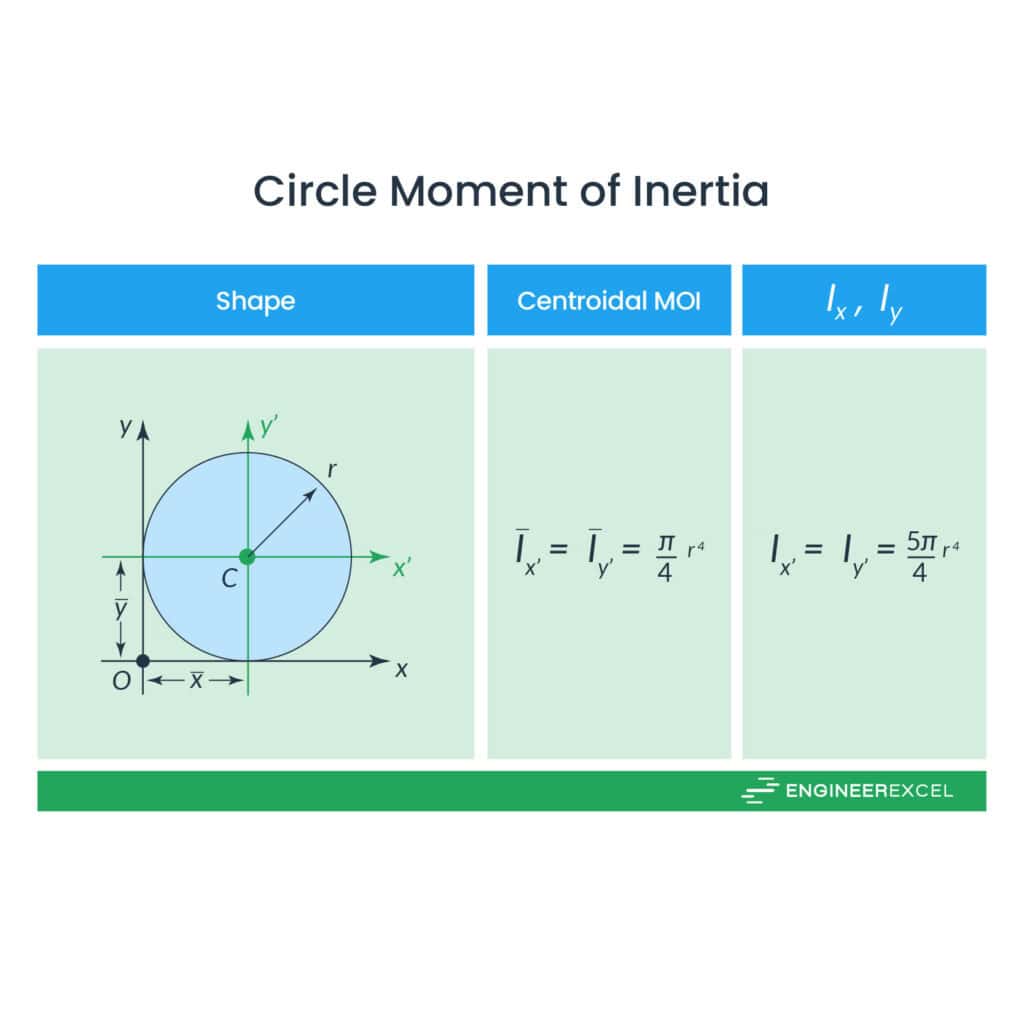
Circle Moment of Inertia
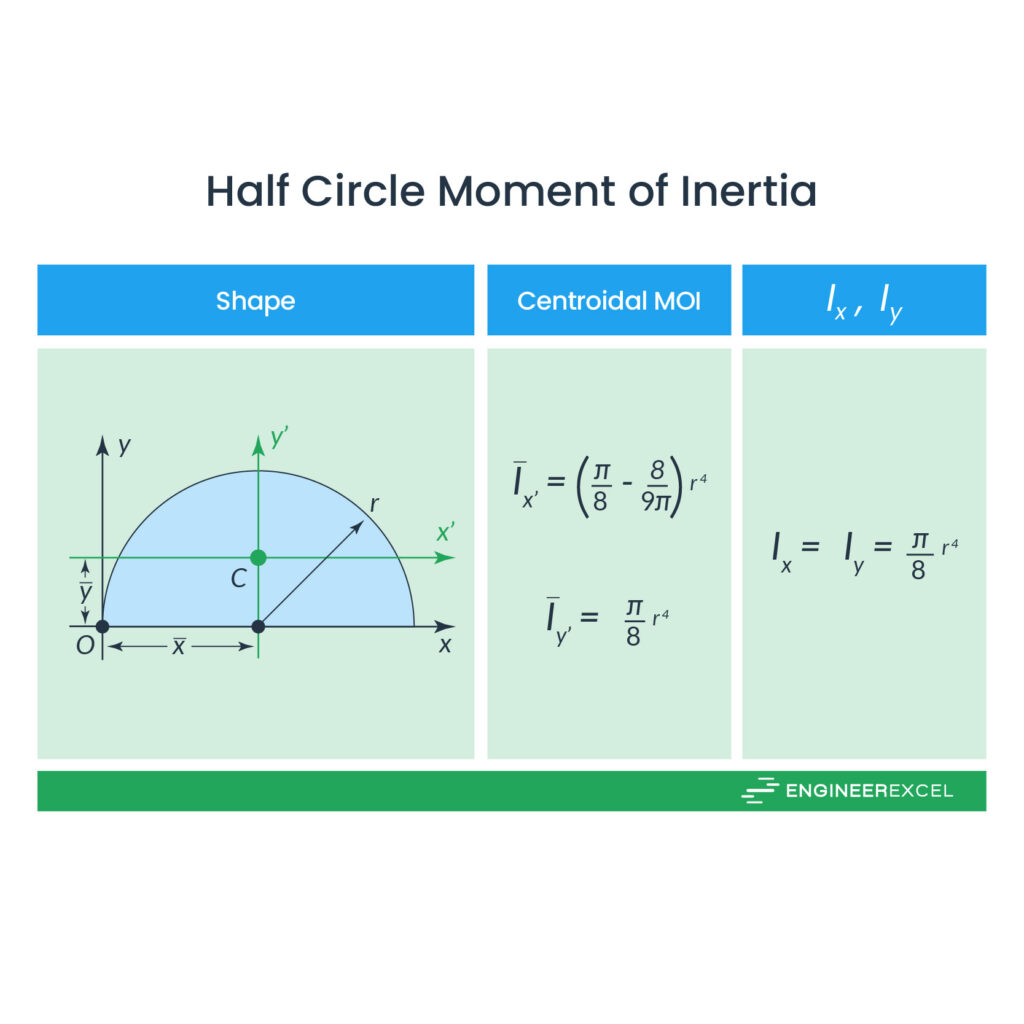
Half Circle Moment of Inertia
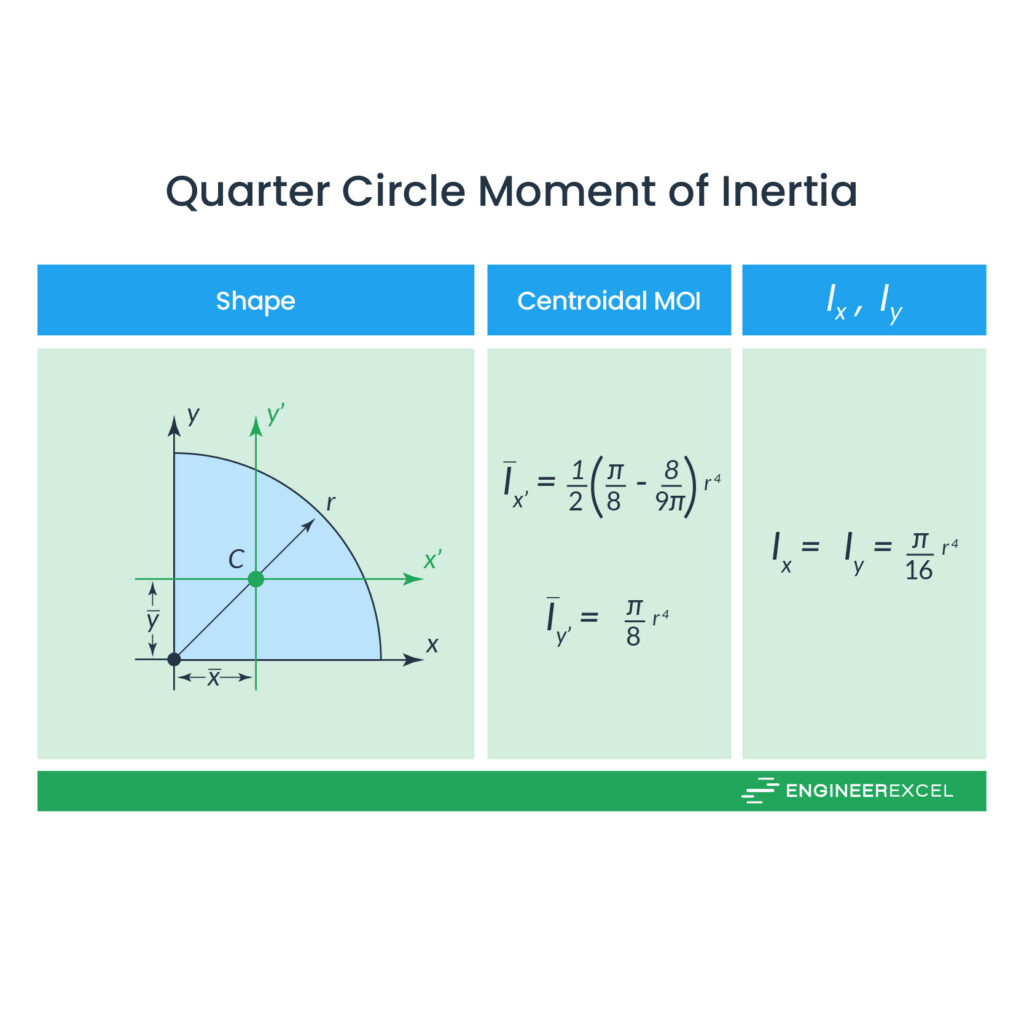
Quarter Circle Moment of Inertia
Combining Moments of Inertia
The total moment of inertia of a body can be determined by summing the individual moments of inertia of the mass elements of the body. Therefore, the individual moments of inertia for the common shapes that make up the complex shape of an asymmetric body can be summed to determine the moment of inertia of the body about a common axis.
After determining the moment of inertia about the central axis, the correction factor dA2 can be added to the result to find the moment of inertia about which the body rotates.
Parallel Axis Theorem Example
The following shape can be divided into individual common shapes:
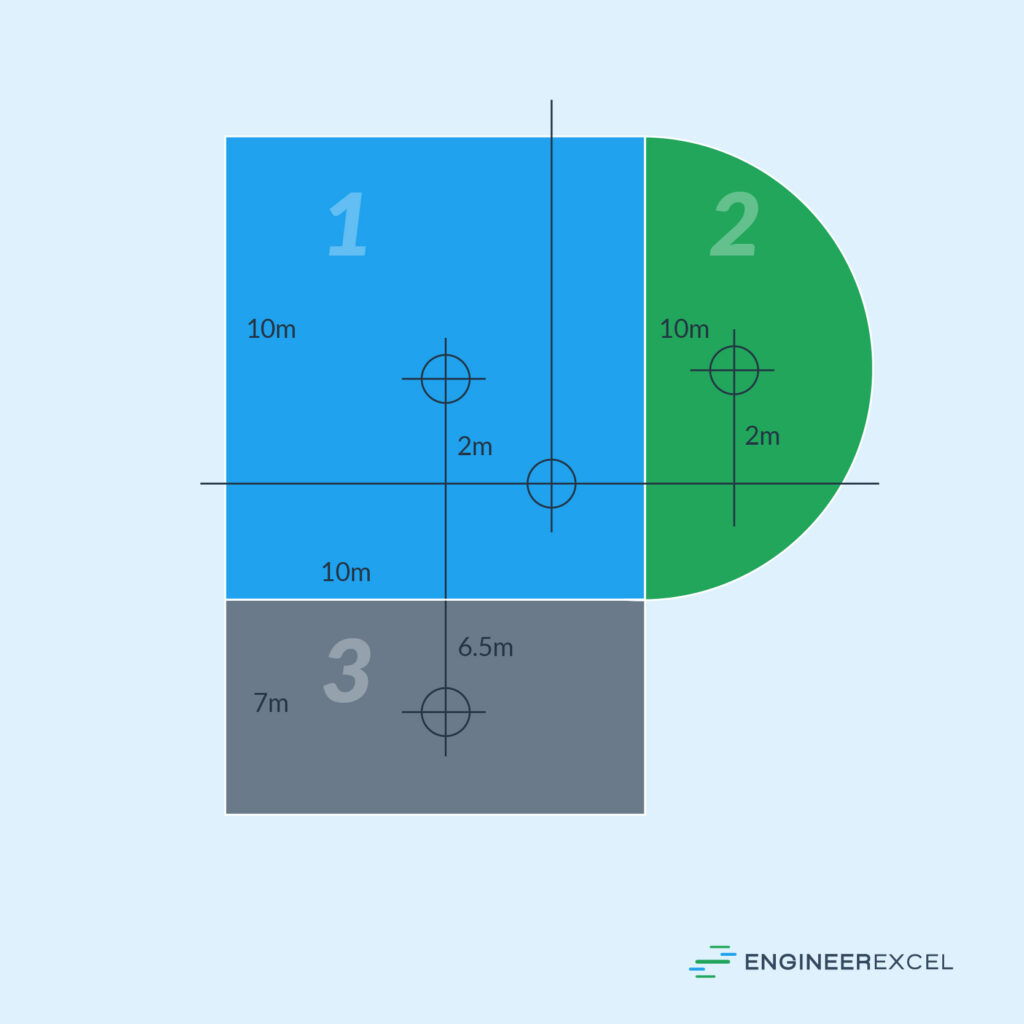
The moment of inertia of area 1 is calculated by:

The moment of inertia of area 2 is calculated by:
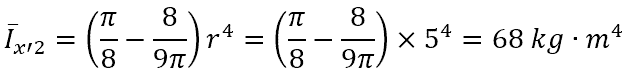
The moment of inertia of area 3 is calculated by:
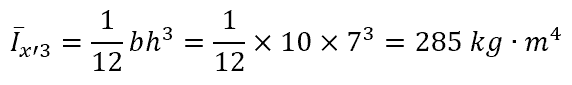
Using the parallel axis theorem, the three moments of inertia are:
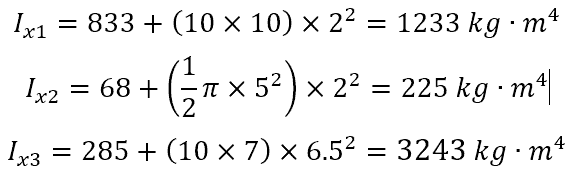
Summing the three: