Moment of Inertia of C Channel

A C channel is a common structural element that is often used in building things such as bridges, walls, or in metal frames. As part of the engineering design of these structures, understanding how a C channel will respond to various forces and loads is necessary. A key parameter of any structural member is its moment of inertia to understand how that member will bend or flex due to a load. Therefore, calculating the moment of inertia of a C channel is important.

Calculating The Moment Of Inertia Of A C Channel

To calculate the moment of inertia of a C channel, there are several steps that need to be carried out. First, the C channel needs to be split into separate pieces for analysis and the area of each of these pieces needs to be determined. Then, the center of gravity of the C channel needs to be found so that the moment of inertia about the centroid can be evaluated. Each of these steps is introduced in detail below.

Splitting the C channel

Often, when calculating the moment of inertia of a complex shape, dividing the shape into different pieces is the most effective means for evaluating the total moment of inertia. For a C channel, such as the one shown in the following figure, separating it into three individual rectangles is appropriate.

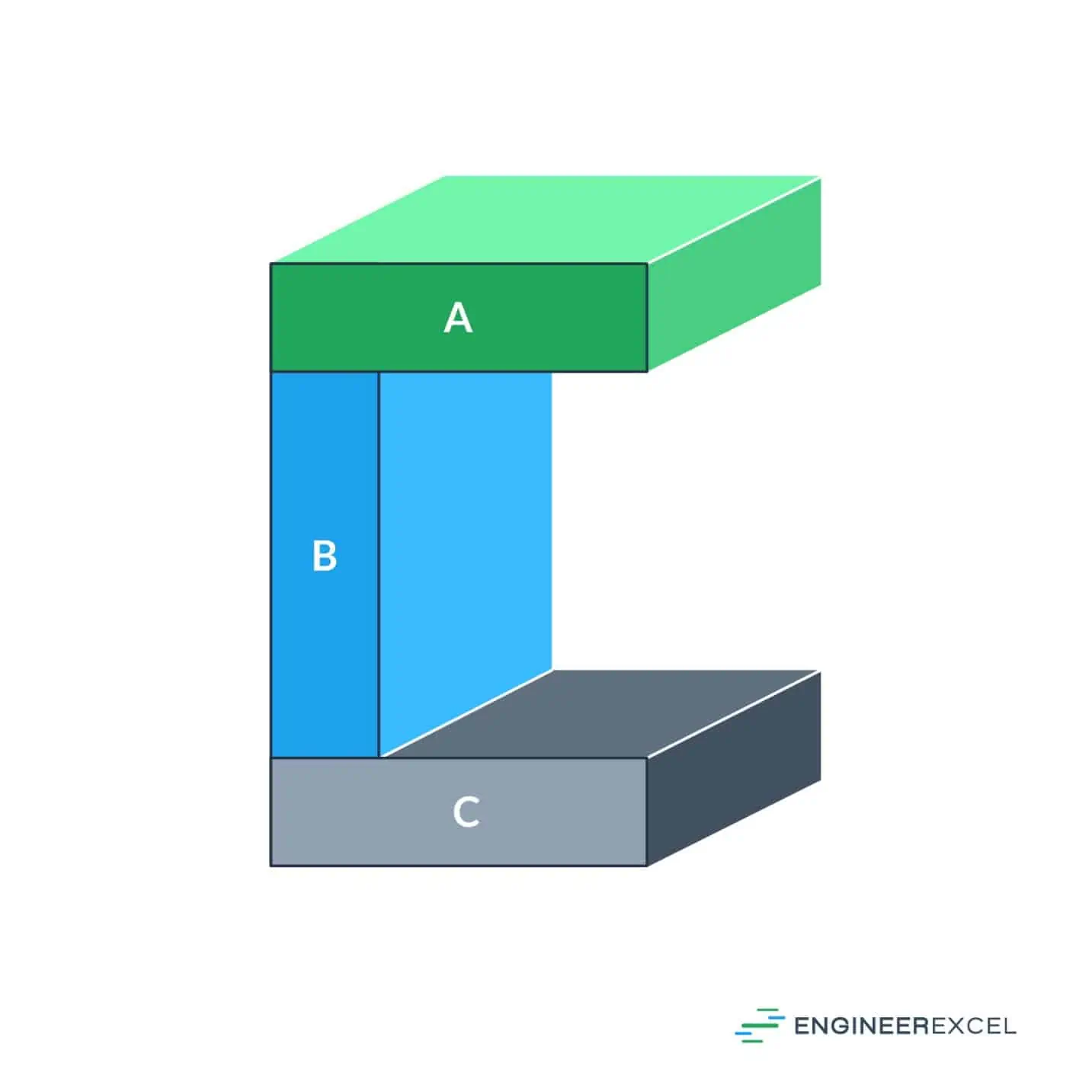
The area of each piece of the C channel, A, B, and C is calculated as its individual width times height. Using the area of each section, the center of gravity is found.

Calculating the center of gravity of a C channel

A C channel is symmetric about its x-axis, but not about its y-axis. However, using the following equation, the location of the y­-axis centroid can be determined:

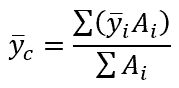
where:

• ȳ_c is the location of the y-axis centroid of the C channel, with SI units of mm
• ȳ_I is the location of the y­-axis centroid of one of the pieces, with SI units of mm
• A_i is the area of one of the pieces, with SI units of mm²

Example Calculation

As an example of locating the y-axis centroid, take a C channel that is dimensioned as follows:

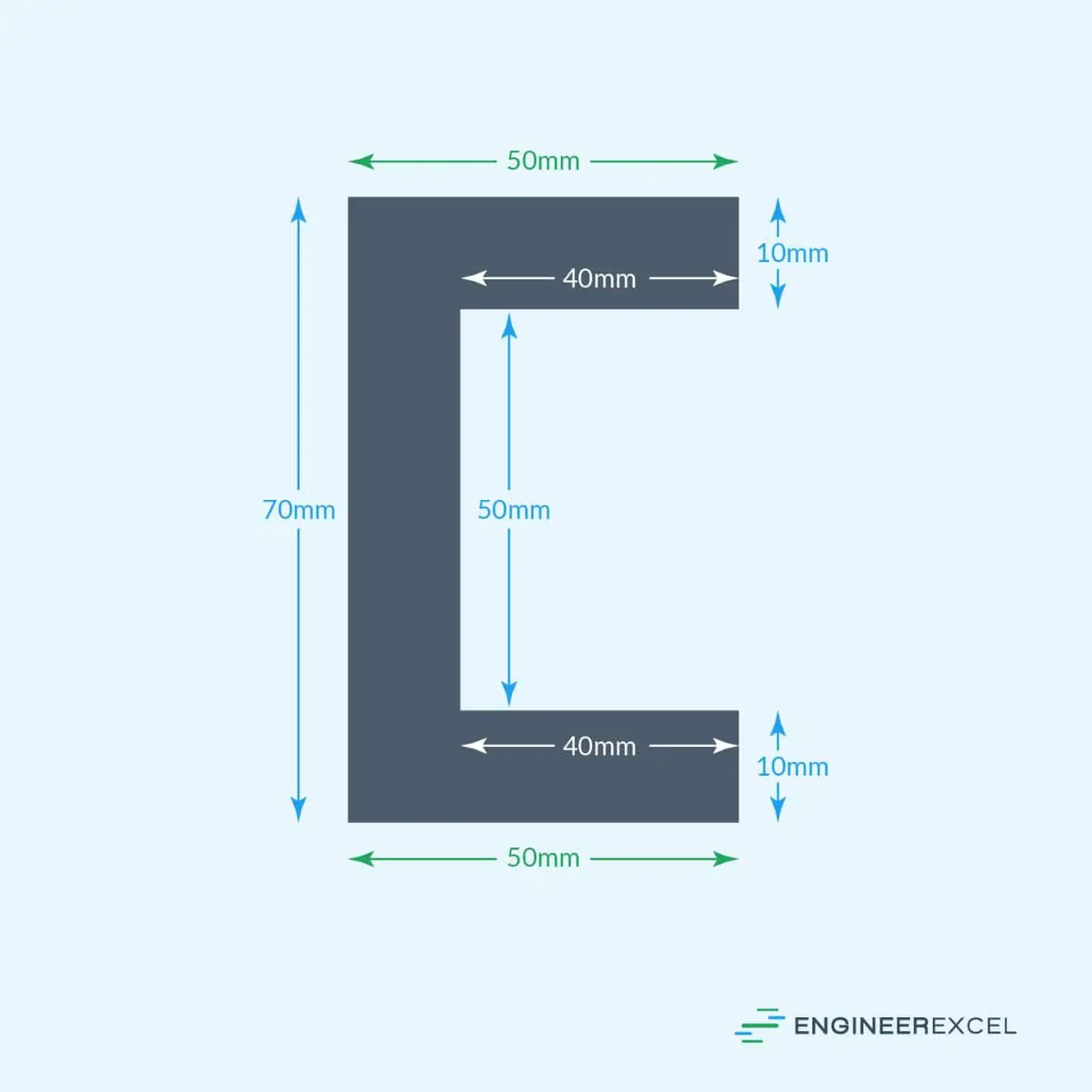
Splitting the C channel into three rectangles, A, B, and C, with the following dimensions:

• A = 10 mm × 50 mm
• B = 50 mm × 10 mm
• C = 10 mm × 50 mm

The location of the y-axis centroid for each piece is as follows:

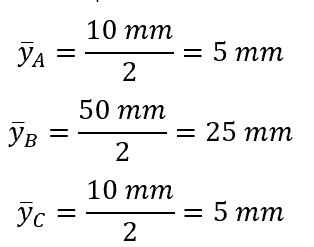
Then, using the equation for ȳ_c:

Now that the preliminary steps have been carried out, the moments of inertia about the x– and y­-axis can be calculated for the C channel.

Calculating The Moment Of Inertia About The X-Axis

The moment of inertia of a C channel about its x-axis can be calculated as follows:

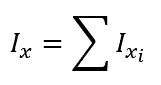
where:

• I_x is the moment of inertia for the entire C channel about its x-axis, with SI units of mm⁴
• I_xi is the moment of inertia of each section about its individual x-axis, with SI units of mm⁴

The moment of inertia of a rectangle about its x-axis is calculated using the following equation:

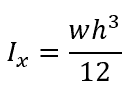
where:

• w is the width of the rectangle, with SI units of mm
• h is the height of the rectangle, with SI units of mm

Because each piece of the C channel is located at a different distance from the x-axis, it is necessary to use the parallel axis theorem to determine each piece’s moment of inertia about the x-axis of the complete channel. The parallel axis theorem is introduced as follows:

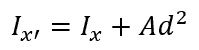
where:

• I_x’ is the moment of inertia of the section about the overall x-axis, with SI units of mm⁴
• I_x is the moment of inertia of the section about its own x-axis, with SI units of mm⁴
• A is the area of the section, with SI units of mm²
• d is the distance from the x-axis of the section to the overall x-axis, with SI units of mm

After the moment of inertia about the overall C channel x-axis is determined for each section, they can be added together to determine the total moment of inertia about the x-axis for the C channel.

Example Calculation

Continuing to use the above C channel, the moment of inertia about the x-axis can be calculated using the following steps:

1. Calculate the moment of inertia of each section about its own x-axis:

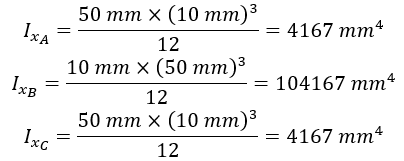
1. Locate the x-axis of each section:

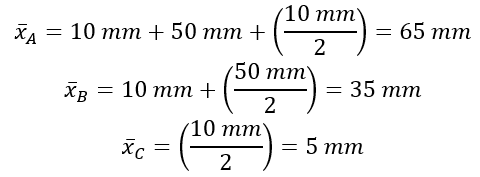
1. Calculate the distance d from the total x-axis for each section:

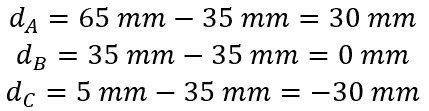
1. Use the parallel axis theorem to determine the moment of inertia for each section about the overall x-axis:

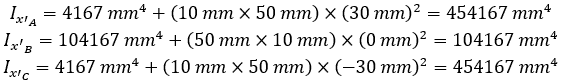
1. Sum all individual moments of inertia to determine the total moment of inertia for the C channel about its x-axis:

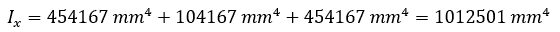
Calculating The Moment Of Inertia About The Y-Axis

Similar to calculating the moment of inertia about the x-axis, the moment of inertia of a C channel about its y-axis can be determined by summing the individual section moments of inertia:

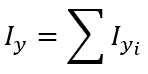
The equation for the moment of inertia of a rectangle about its y-axis is calculated as follows:

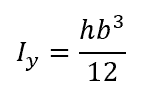
Again, the parallel axis theorem is used to find the moment of inertia of each section about the overall y-axis of the C channel, substituting the distance from the y-axis calculated previously for the distance from the x-axis.

Example Calculation

Continuing to use the above C channel, the moment of inertia about the y-axis can be calculated using the following steps:

1. Calculate the moment of inertia of each section about its own y-axis:

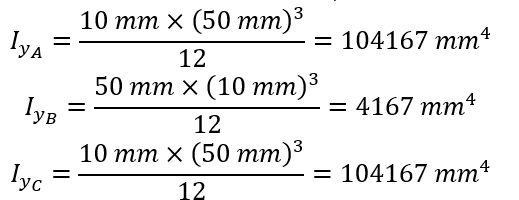
1. Locate the y-axis of each section:

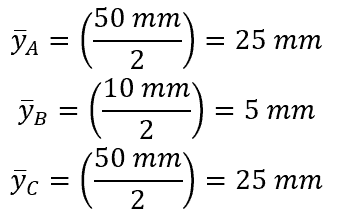
1. Calculate the distance d from the total y-axis for each section:

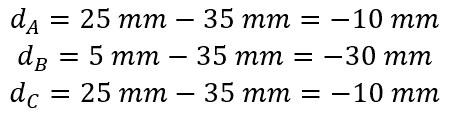
1. Use the parallel axis theorem to determine the moment of inertia for each section about the overall y-axis:

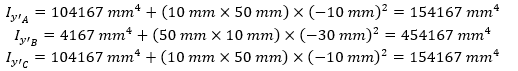
1. Sum all individual moments of inertia to determine the total moment of inertia for the C channel about its y-axis: