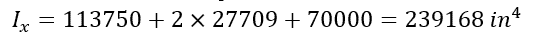Moment of Inertia of Tubes

In engineering design, tubes are often used as structural members. Understanding how those members will respond to forces and moments is important for optimizing the overall design. The moment of inertia of a tube is used to express how well it will withstand those forces and moments.

Circular tubes and rectangular tubes are used, depending on the situation, and the calculation of the moments of inertia of these types of tubes is different.

Moment Of Inertia Of Tubes

Regardless of the shape of the tube, the moment of inertia is used in engineering design to determine how the tube will respond to forces and moments that cause bending. A tube with a higher moment of inertia will resist those forces and moments better than a tube with a lower moment of inertia, which means that there will be less bending stress in the tube.

In optimizing an engineering design, choosing the dimensions of the tube to withstand expected loads can help minimize the overall weight of the tube, which can reduce costs.

Circular Tube Moment Of Inertia

The moment of inertia of a circular tube is a function of the outer radius, r_o, and the inner radius, r_i, as shown in the following figure:

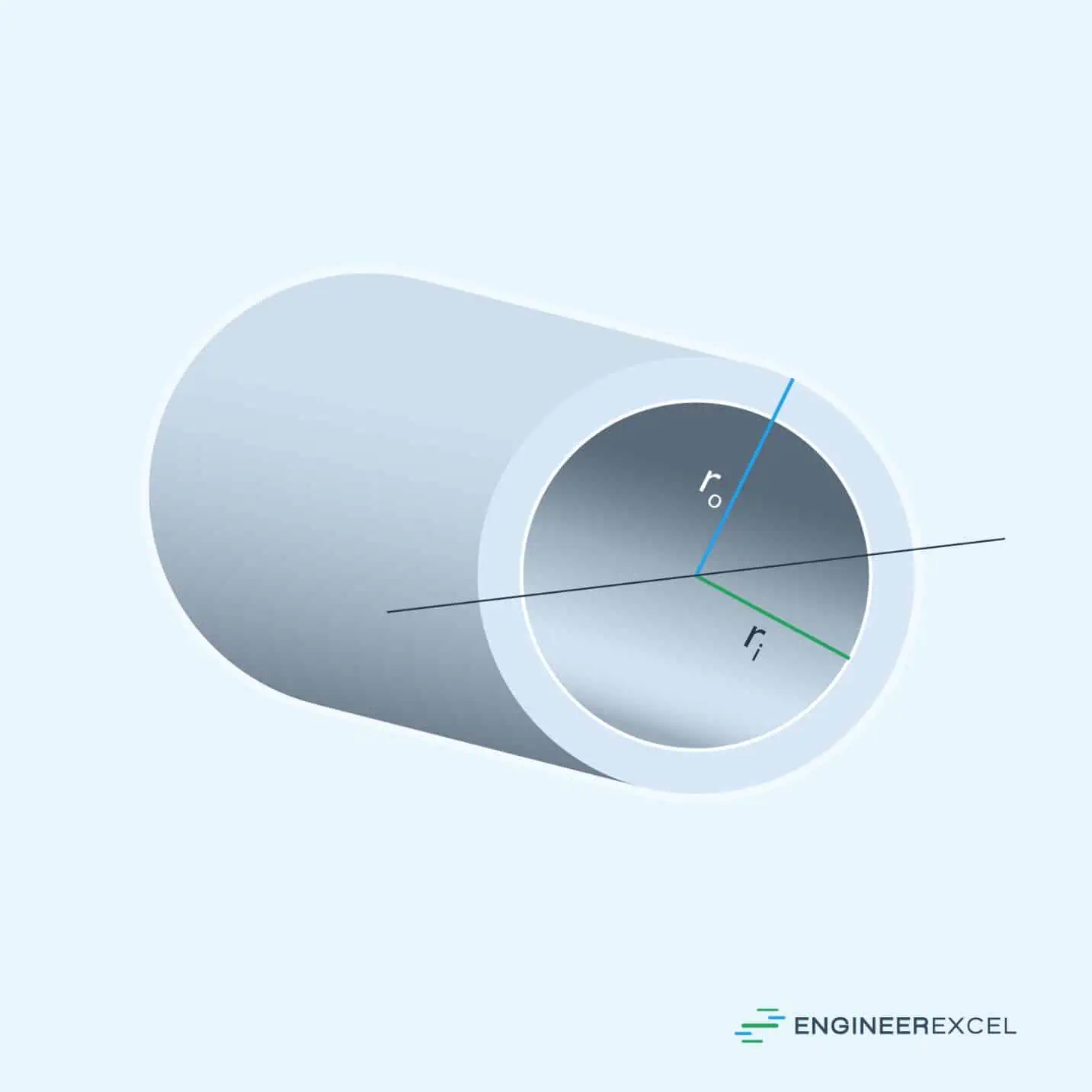
Alternatively, the outer diameter and the wall thickness, t, may be given, where the thickness is simply the outer radius minus the inner radius. To calculate the moment of inertia for a circular tube, the following equation is used:

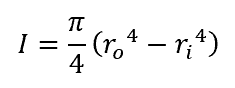
where:

• r_o is the outer radius, with units of in
• r_i is the inner radius, with units of in
• I is the moment of inertia, with units of in⁴

In the case of a typical circular tube, the moment of inertia about the x-axis will be equal to that about the y-axis, and both will pass through the centroid of the tube.

Example For A Circular Tube

Taking a circular tube with an outer radius of 20 in and an inner radius of 18 in, the moment of inertia is calculated as follows:

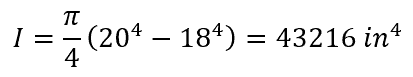
Rectangular Tube Moment Of Inertia

The moment of inertia of a rectangular tube is a function of the width, w, and height, h, of the tube and the tube thickness, t, as shown in the following figure:

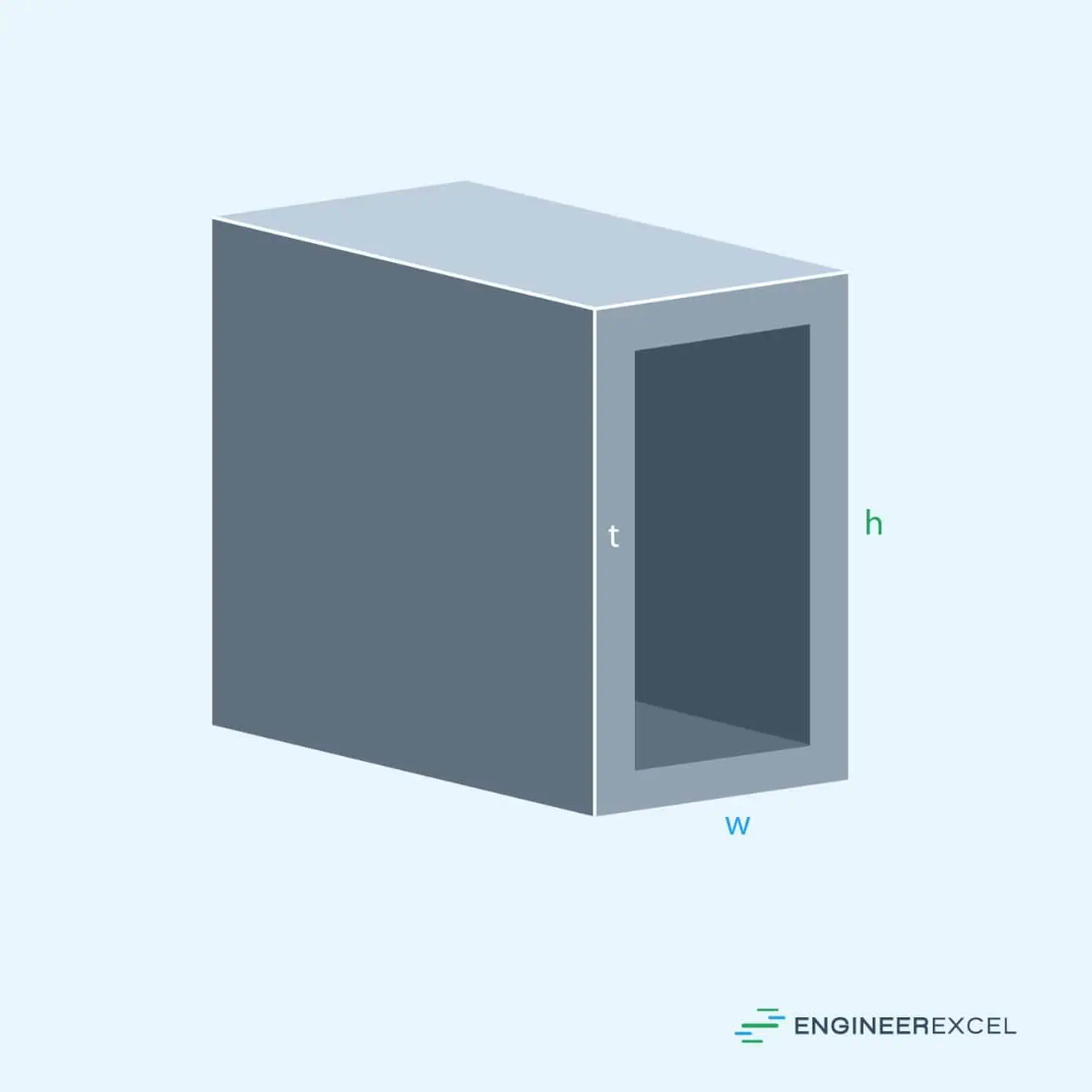
Unlike a circular tube, the moment of inertia of a rectangular tube is different about the x-axis than about the y-axis. To calculate the moment of inertia about the x-axis, the following equation is used:

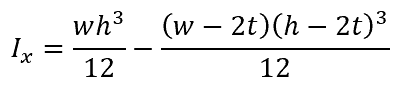
where:

• w is the width of the tube, with units of in
• h is the height of the tube, with units of in
• t is the thickness of the tube, with units of in
• I_x is the moment of inertia about the x-axis, with units of in⁴

Similarly, the moment of inertia about the y-axis is calculated as follows:

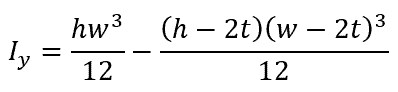
Example For A Rectangular Tube

Taking a rectangular tube with a width of 30 in, a height of 50 in, and a thickness of 5 in, the moments of inertia are calculated as follows:

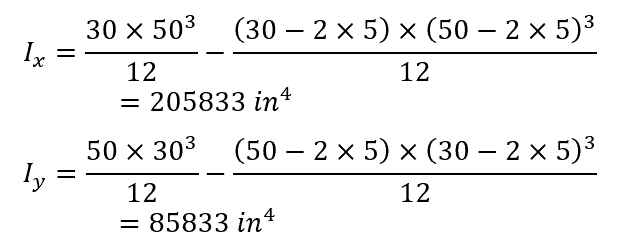
Moment Of Inertia For Rectangular Tube With Different Thickness

In practical engineering applications, a rectangular tube with different thicknesses on the sides and the top and bottom may be used. Such a tube is shown in the following image:

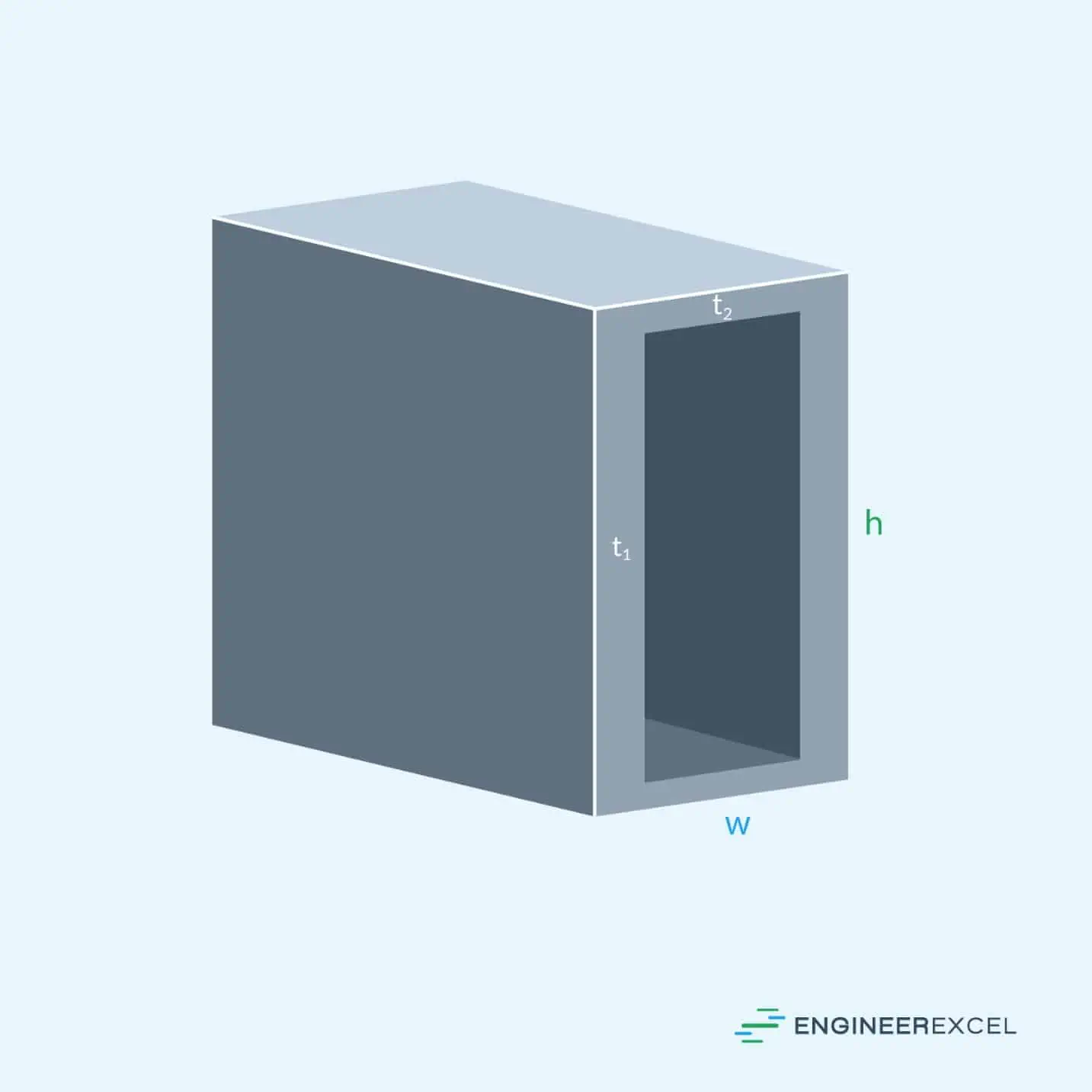
In the event that the wall thicknesses are not the same, the moment of inertia equations are changed as follows:

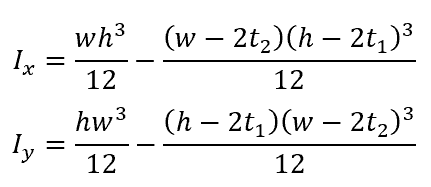
Example Calculation For Rectangular Tube With Different Thicknesses

For a rectangular tube with the same width and height as the previous example but with t₁ equal to 10 in and t₂ equal to 5 in, the moments of inertia are:

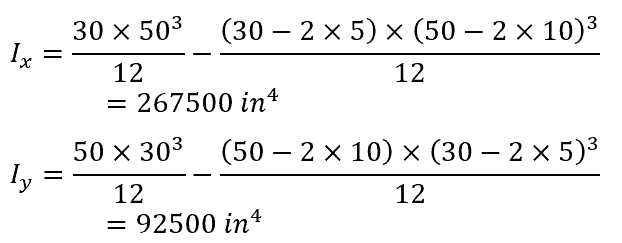
Moment Of Inertia For Unsymmetric Rectangular Tube

Previously, rectangular tubes that were symmetric about the x-axis and the y-axis were discussed. For example, if the bottom wall thickness is larger than the top wall thickness, the tube will not be symmetric about the x­-axis. This is shown in the following figure:

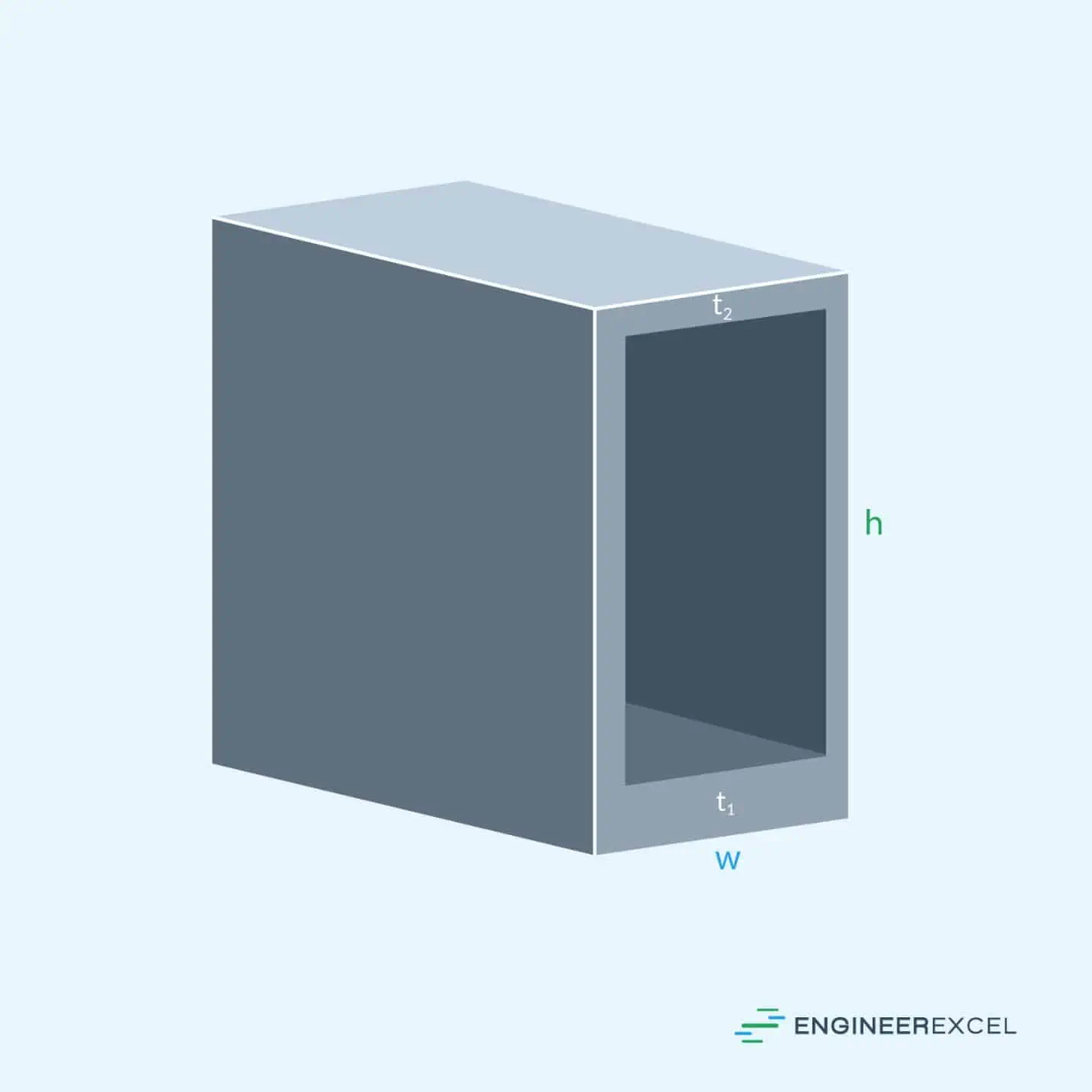
To calculate the moment of inertia about the x-axis, it is necessary to use the parallel axis theorem, which is applied via the following equation:

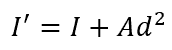
where:

• I’ is the moment of inertia about an arbitrary axis that is parallel to the axis through the centroid
• A is the area of the tube, with units of in²
• d is the distance from the arbitrary axis to the axis through the centroid, with units of in

To determine the distance between the two axes, it is necessary to divide the shape of the tube into individual pieces, as shown in the following:

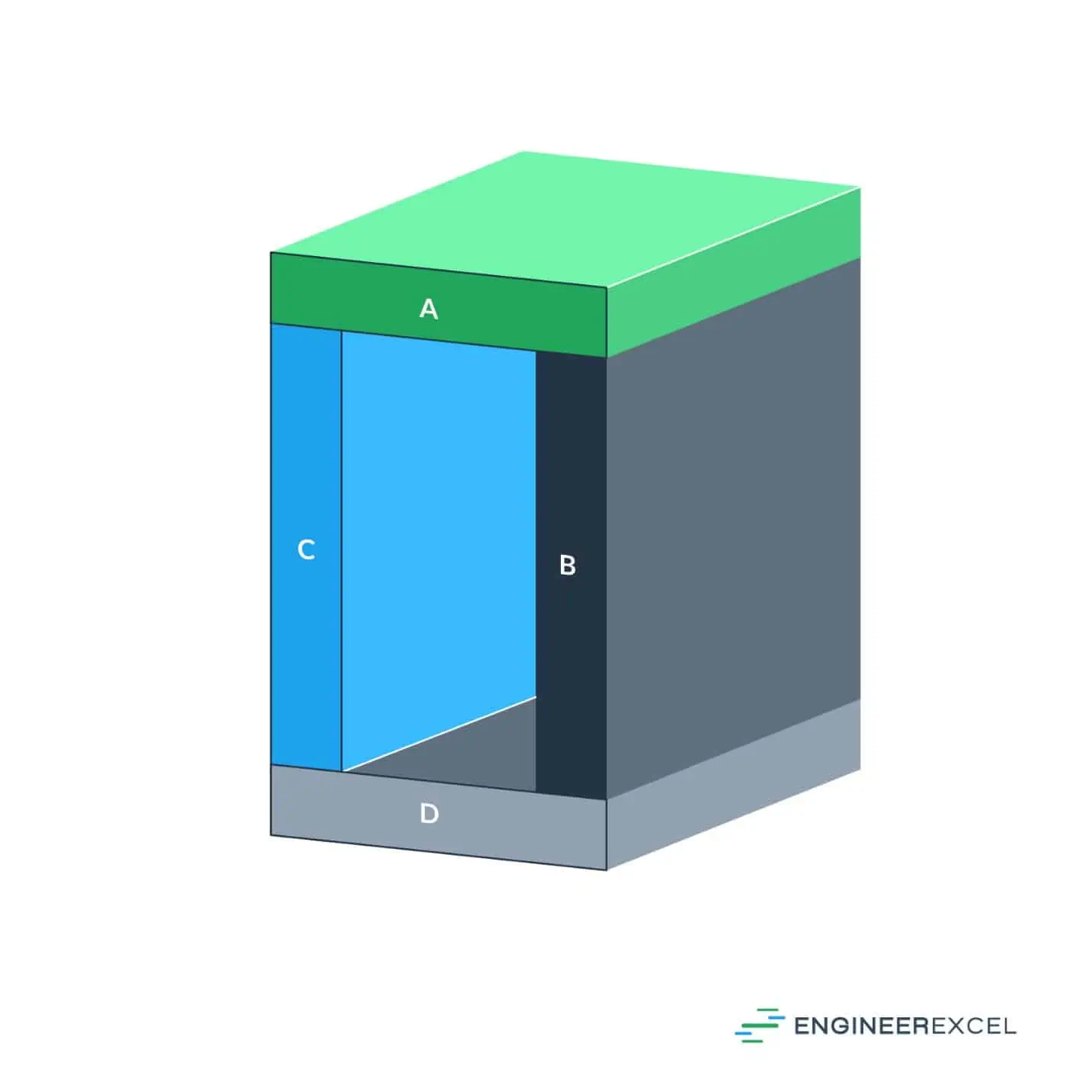
Using this information, the location of the x-axis of the overall shape can be calculated using the following equation:

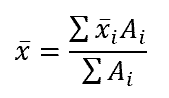
where:

• x̄ is the overall x-axis location, with units of in
• x̄_I is the individual x-axis location, with units of in
• A_i is the individual area, with units of in²

Example Calculation For Unsymmetric Rectangular Tube

To calculate the moment of inertia about the x-axis using the parallel axis theorem, a rectangular tube with a width of 30 in, a height of 50 in, a thickness at the top and sides of 5 in and a bottom thickness of 10 in is used as an example. The calculation process is as follows:

1. Calculate the moment of inertia of each section:

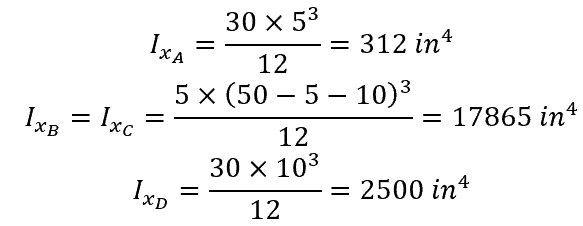
1. Calculate the area of each section:

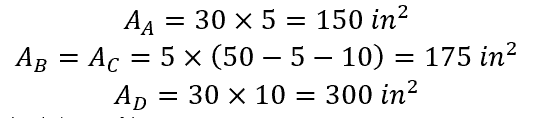
1. Calculate the location of the x-axis:

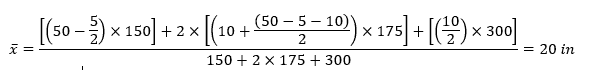
1. Calculate the distance of the individual x-axis from the overall x-axis for each piece:

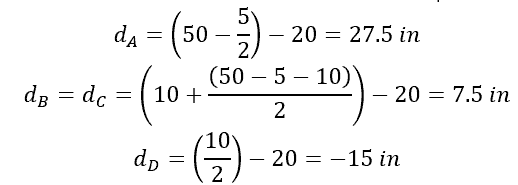
1. Apply the parallel axis theorem to each piece:

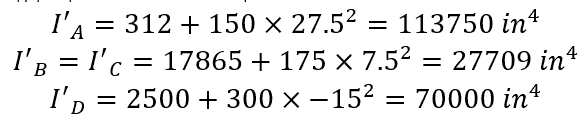
1. Add all individual moments of inertia to get the total moment of inertia about the x-axis: