Thermal stress refers to the stress induced in a material due to changes in temperature, leading to expansion or contraction within the material. If left unmanaged, this phenomenon can result in structural deformation or failure in materials subjected to varying temperatures. In this article, we will discuss thermal stress, including the factors influencing it, its calculation, and methods for measurement.
What is Thermal Stress
Thermal stress refers to the internal force that develops within a material as a result of thermal expansion or contraction. When a body experiences temperature changes, it undergoes physical alterations in its dimensions. Typically, an increase in temperature will cause the body to expand, whereas a decrease will result in contraction.
This dimensional change is generally proportionate to the temperature variation, as shown in the following equation:
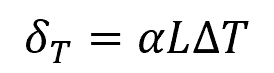
Where:

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
- δT = change in length of the material due to temperature change [m]
- α = coefficient of expansion [K-1]
- L = original length of the material [m]
- ΔT = change in temperature [K]
The coefficient of thermal expansion (α) characterizes the rate at which a material expands or contracts with temperature change. Each material has a specific coefficient that can be referenced from material property tables.
In statically determinate systems, materials are free to expand or contract, and thus thermal stress may not develop. However, in statically indeterminate structures, these thermal deformations are restricted by support conditions or connectivity to other structural components, invariably leading to the development of internal stresses—termed thermal stresses.
Calculating Thermal Stress
The thermal and load-displacement relationship can be used to calculate the thermal stress in an indeterminate system.

Consider the scenario of a bar fixed between two supports, as depicted above. In this case, any thermal displacement resulting from a change in temperature would be balanced out by support reactions that act to restore the bar to its original position. Mathematically:
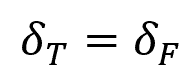
Where:
- δF = change in length of the material due to the internal force [m]
The above equation can be re-written as:
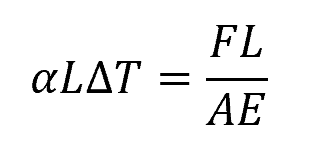
Where:
- F = internal force [N]
- A = cross-sectional area of the bar [m2]
- E = modulus of elasticity of the material [N/m2]
Rearranging the above equation, the formula for the internal force associated with thermal stress becomes:
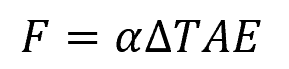
We can then divide the internal force by the cross-sectional area to calculate for the thermal stress:
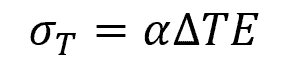
Where:
- σT = thermal stress [Pa]
Analysis of thermal stresses is important to ensure the integrity and longevity of engineering designs, particularly structures or components experiencing a range of temperatures due to environmental conditions or operational requirements.
Factors Influencing Thermal Stress
The degree to which materials experience thermal stress is governed by their inherent properties, including material properties,
Material Properties
Material properties, such as the coefficient of thermal expansion, affect the thermal stress that a structural component experiences. The coefficient of thermal expansion is a material-specific value that quantifies how much a material expands or contracts with a change in temperature. For isotropic materials, which have properties that are the same in all directions, this coefficient is uniform, but for anisotropic materials, such as composites, the coefficient can vary depending on the direction of measurement.
Materials with a high coefficient of thermal expansion will expand or contract more with temperature changes. Conversely, materials with a low coefficient are more stable and less prone to size changes with temperature fluctuations.
In addition to the coefficient of thermal expansion, thermal conductivity, which is a measure of a material’s ability to conduct heat, also affects thermal stress. It is denoted by the symbol k and typically measured in W/(m·K). Materials with high thermal conductivity disperse heat quickly, which results in more uniform temperature distribution and, consequently, reduced thermal stress.
The specific heat capacity, which indicates the amount of energy required to raise the temperature of a unit mass of a substance by one degree, also affects thermal stress. A high specific heat capacity suggests that the material can absorb more heat before its temperature rises significantly, thus affecting the rate of thermal stress development.
Lastly, the modulus of elasticity affects the amount of thermal stress induced by a given strain. Materials with higher moduli are stiffer and can withstand higher stresses.
Restraint Conditions
If a material is constrained and not allowed to freely expand or contract, the resulting thermal stress will be higher. This can occur due to structural design, such as when materials are fixed in place or connected to other materials with different coefficients of thermal expansion.
Temperature Profile
The magnitude of the temperature change that a material undergoes is directly proportional to the thermal stress experienced. Greater temperature changes result in higher thermal stresses.
Furthermore, the presence of temperature gradient within a material (i.e., when one part of the material is hotter than another) can cause differential expansion, leading to thermal stress even if the average temperature change is not extreme.
Measurement and Analysis
Experimental Methods
Thermal stress can be experimentally determined using instruments like strain gauges and infrared thermography. Strain gauges, affixed to a material’s surface, measure expansion or contraction due to temperature changes, while infrared cameras capture temperature distributions, thereby identifying hotspots that indicate stress concentrations.
Numerical Analysis
Numerical analysis uses mathematical models to predict stress due to thermal loads. Engineers commonly use the Finite Element Method (FEM), as it provides detailed insights into stress distribution within complex geometries. The FEM process involves creating a mesh over the part’s geometry and solving the governing equations at each node.
Thermomechanical Simulation
Thermomechanical simulation combines thermal loading with mechanical analysis to assess a material’s response under operating conditions. Software such as ANSYS models the coupled thermal-mechanical effect. Key simulation steps include defining material properties, applying boundary conditions, and loading cases.
