Since a worksheet is essentially a gigantic matrix, it’s no surprise that matrix multiplication in Excel is super easy – we just need to use the MMULT Excel function.
Matrix Multiplication with the MMULT Excel function
You can multiply matrices in Excel thanks to the MMULT function. This array function returns the product of two matrices entered in a worksheet.
The syntax for the function is:
MMULT(array1,array2)
where array1 and array2 are the arrays or matrices to be multiplied.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
The result of the MMULT function is an array with a number of rows that’s the same as array1 and a number of columns that is the same as array2.
If you are using Excel 365, MMULT is a dynamic array function. This means that you can enter a formula using MMULT into a single cell, and Excel will automatically expand the range to fit the result of the function.
If you are NOT using Excel 365, MMULT must be entered as an array function by selecting the appropriate number of cells for the result array and typing CTRL+SHIFT+ENTER.
Matrix Multiplication Rules
To perform matrix multiplication in Excel effectively, it’s helpful to remember how matrix multiplication works in the first place. So, let’s say we have two matrices, A and B, as shown below:
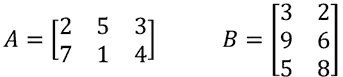
The product of these two matrices (let’s call it C), is found by multiplying the entries in the first row of column A by the entries in the first column of B and summing them together. This is also known as the dot product. This single value becomes the entry in the first row and first column of matrix C.

We continue doing this until we’ve found the dot product for each row and column combination.
Since we multiply the rows of matrix A by the columns of matrix B, the resulting matrix C will have a size of 2 x 2. Or more generally, the matrix product has the same number of rows as matrix A, and the same number of columns as matrix B.
Because of the way matrix multiplication works, it’s also important to remember that we can only multiply two matrices if the number of rows in B matches the number of columns in A.
Got it?
If not, that’s ok. Hopefully a few examples will clear things up. 🙂
Excel Matrix Multiplication Examples
Matrix Multiplication as an Array Function (All Versions of Excel)
Let’s take the matrices from above and find the product using matrix multiplication in Excel with the MMULT function:
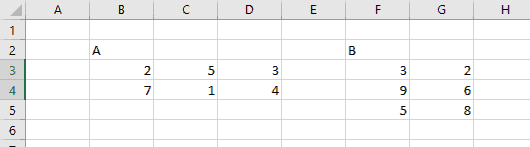
First, let’s find C, the product of AB.
Since MMULT is an array function, it will return values to more than one cell.
We know that the result is going to be a 2×2 matrix because the first matrix, A, has two rows and the second matrix, B, has two columns.
So, if we were working in Excel 365 or any previous version of Excel, we select an area on the worksheet 2 cells wide by 2 cells high:
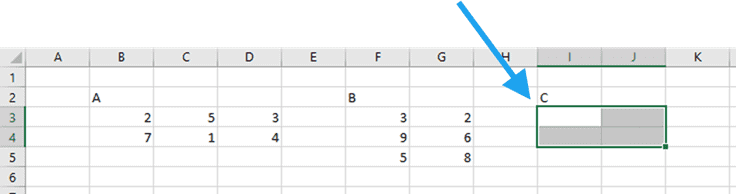
Next, with the area still selected, type the array formula and select the arguments (I assigned names to the matrices A and B):

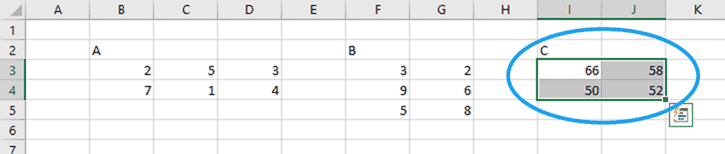
Finally, type CTRL+SHIFT+ENTER (because it’s an array formula) to return the resulting matrix product:
Matrix Multiplication as a Dynamic Array Function (Excel 365 Only)
In Excel 365, it’s not necessary to select the correct number of return cells or type CTRL+SHIFT+ENTER. Simply enter the array formula in the upper left most cell of the array and Excel will dynamically fill all the resulting values:

Other MMULT Examples in Excel
What if, instead of calculating matrix C, by multiplying matrix A times B, we calculated a different matrix D, by multiplying matrix B times A?
Since the first matrix, B, has 3 rows, and the second matrix, A, has 3 columns, matrix D would have 3 rows and 3 columns. So, we would start with a selection 3 cells wide and high:

Then, type in the formula for MMULT, selecting B as array1 and A as array2…

… and type CTRL+SHIFT+ENTER to obtain matrix D:
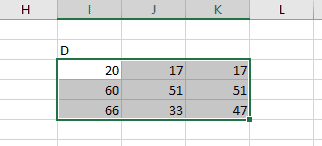
The MMULT function also works for multiplying a matrix (A) by an array (x). Of course, the rule still stands that the number of rows in x must match the number of columns in A.
The result is an array, F, that has 1 column and the same number of rows as A:

MMULT Excel Errors (Why is MMULT not working in Excel?)
There are a few different ways that you can get errors in Excel with the MMULT function:
MMULT #VALUE! Error
A #VALUE! error will occur when the number of columns in array 1 (A below) is not the same as the number of rows in array2 (x below).
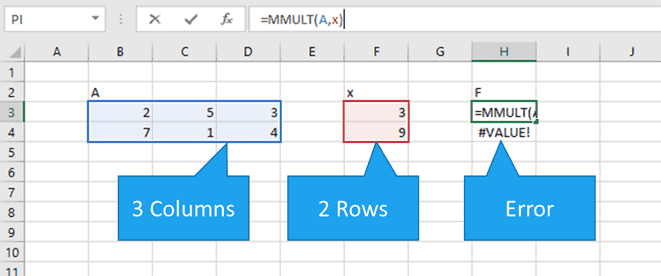
To fix this would require that array x has three rows, so it probably means that one of the values from array x is missing.
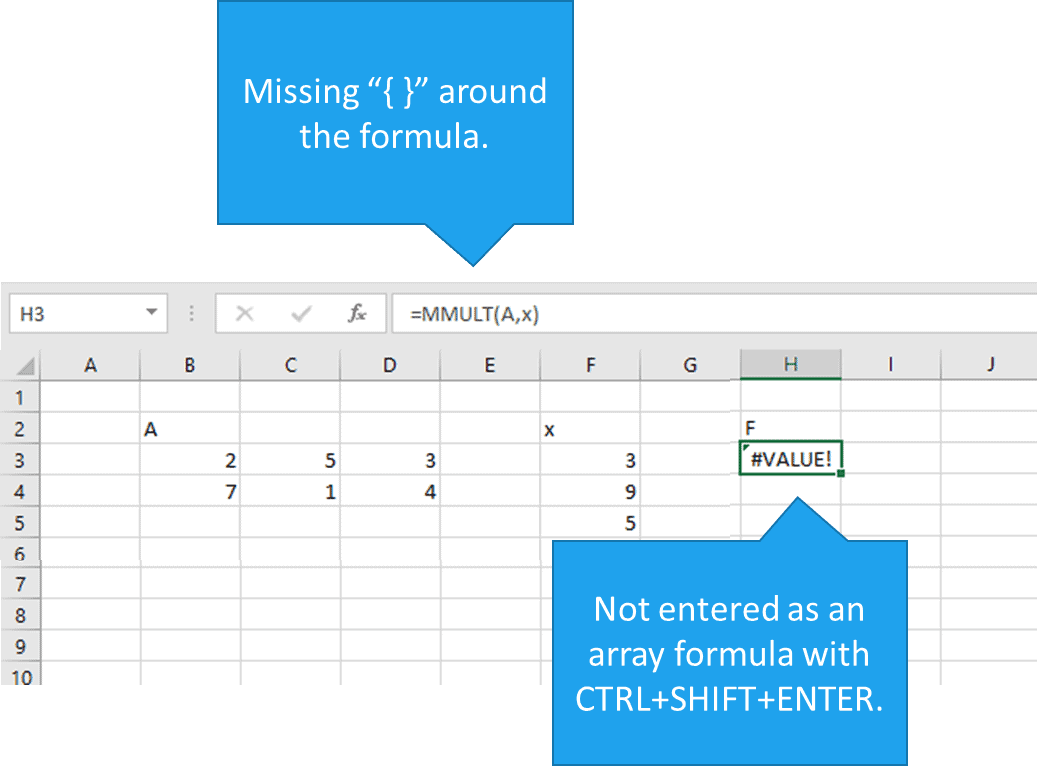
If you are not using Excel 365 and MMULT is not entered as an array formula by typing CTRL+SHIFT+ENTER, it will also return a #VALUE! error to a single cell:
Finally, a #VALUE! Error will also occur if any of the elements in either array1 or array2 do not contain numbers.

MMULT Returns a Single Value
If you are not using Excel 365 and MMULT returns a single value, it’s because only a single cell was chosen for the resulting array. In earlier versions of Excel, it’s up to the user to select the appropriate number of cells for Excel to return a result to. If a single cell is selected, MMULT will perform the matrix multiplication and return the first value in the result array to that cell.
It’s also possible for this behavior to occur in Excel 365 if a single cell is selected for the result and the MMULT function is entered as an array formula by typing CTRL+SHIFT+ENTER.
MMULT Returns Too Many Values
Although not always an error, MMULT can return some surprising results when the output area for the function is larger than required.
Adding extra columns causes the results to be duplicated:

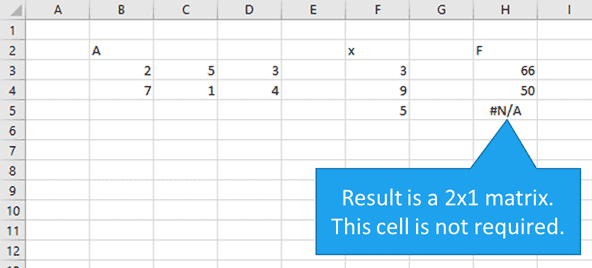
MMULT #N/A! Error
Adding extra rows to the MMULT array causes an #N/A! error to be displayed, although it’s only displayed in the extra cell:
Matrix Multiplication Limits in Excel
There are no software-imposed limits to the size of matrix that can be multiplied in current versions of Excel. Basically, you can multiply matrices as large as you want provided you have enough RAM in your computer.
However, if you’re still using Excel 2003 or earlier, you’ll be restricted to an output of 5046 cells when using the MMULT function (roughly a 71×71 matrix).
Even if you are in newer versions of Excel, there is one caveat: you cannot create an array that fills an entire column of a worksheet. Since there are 1,048,576 rows in a worksheet in Microsoft Excel 2007 and later, I guess this does constitute a limit on matrix multiplication in Excel.
This article from Microsoft support has some helpful information on the limitations of Excel when working with arrays.
