Fluid dynamics – and more specifically, fluid flow – is the study of how fluids (both liquid and gas) move when subjected to unbalanced forces. Flow can either be laminar or turbulent.
Laminar flow occurs when fluid particles are moving together in the same direction in parallel paths. It’s defined as smooth, steady motion where there are no disturbances or eddies. Turbulent flow is characterized by fluid particles that may travel in the same general direction but whose motion is noticeably more chaotic. Rather than traveling in parallel paths, the fluid particles collide and mix, creating eddies and disturbances. Turbulent flow usually results from low viscosity fluids moving at high velocities.
This article will describe the differences between laminar and turbulent flows in greater detail, introduce the Reynolds number and explain how it is used, and identify real world applications that incorporate turbulent flow.
Why Flow Becomes Turbulent
The type of fluid flow is primarily dependent on the viscosity of the fluid and the velocity at which it is moving. Laminar flow is smooth and often occurs when fluids are either more viscous or moving at a slower pace.
Imagine a highly viscous fluid like maple syrup being poured from a bottle. Even if the syrup were moving at a high velocity, the syrup is viscous enough that its individual particles would still tend to travel in parallel paths because there is too much friction and resistance for them to overlap. It would take a very high velocity for inertia to overcome the viscous force.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
Turbulent flow occurs when the opposite criteria are met. Flow tends to be turbulent when there is a low-viscosity fluid moving at a high velocity. Low-viscosity fluids have minimal resistance between individual particles so moving at a moderately high velocity generates enough inertia to overcome the resistance between particles. Because the inertia force is dominant, particles are able to move in random directions and mix.
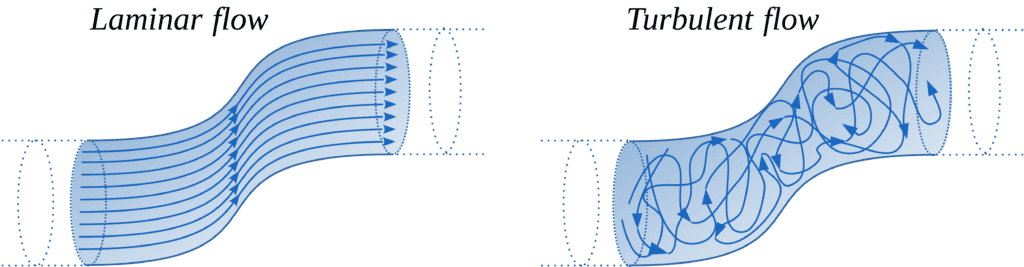
Determining Type of Flow Numerically
Fluid flow is divided into three regimes: laminar, transitional (or critical), and turbulent. The most common method for determining flow regime is to calculate the Reynolds number, which is a unitless value that represents the ratio between inertia forces and viscous forces. This is a numerical interpretation of the correlation between inertia and viscous forces described in the previous section.
Calculating and Using the Reynolds Number
The Reynolds number can be calculated using the following equation:

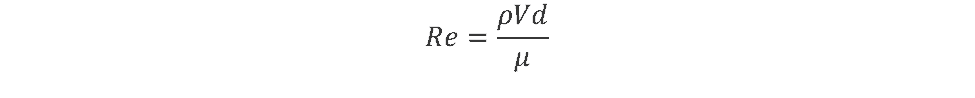
where:
- Re = Reynolds number (unitless)
- V = velocity (m/s)
- d = length or diameter (m)
- µ = viscosity (Ns/m2)
- ρ = density (kg/m3)
- ν = kinematic viscosity (m2/s)
Re < 2000 represents laminar flow, Re > 4000 is turbulent flow, and the range where 2000 > Re > 4000 is referred to as transitional or critical flow.
Viscosity, density, and kinematic viscosity are determined by the fluid itself and therefore are not variable. The only variables in the Reynolds equation that would cause flow to change from laminar to turbulent are velocity and diameter. Those two parameters are directly proportional to the Reynolds number so as velocity and diameter increase, the Reynolds number also increases and flow enters (or approaches) the turbulent range.
Exceptions to the Reynolds Equation
It’s worth noting that the Reynolds equation assumes the fluid being used is incompressible and of constant viscosity. The flow of compressible fluids (gasses) is evaluated using other calculations, including the continuity equation and the Navier-Stokes equation. Fluids that do not have a constant viscosity, known as non-Newtonian fluids, are also treated differently. Non-Newtonian fluids like ketchup, quicksand, and paint will change viscosity based on forces applied to them.
Practical Examples and Analyses Entailing Turbulent Flow
Turbulent flow is encountered in many scientific fields such as engineering, aerodynamics, meteorology, and biology. Some scenarios are straightforward and can be analyzed relatively easily, like trying to calculate friction and flow rate in a pipe. Trying to optimize the shape of a vehicle for aerodynamics (air flow) is a bit more complex and requires different analytical methods.
Computational Fluid Dynamics
Computational Fluid Dynamics, also known as CFD, is a specific branch of fluid mechanics that is used to solve problems related to fluid flow. CFD analysis is used in a variety of science industries, notably aerodynamics, weather simulation, environmental engineering, and heat transfer.
Because turbulent flow is constantly fluctuating and chaotic, it is difficult to analyze numerically. Many people working with fluid problems on a regular basis rely on high-tech computers and software to run simulations and calculations. Simulation software can be used to analyze everything from the airflow around a plane’s landing gear to the projected path of pollution from factory exhausts.
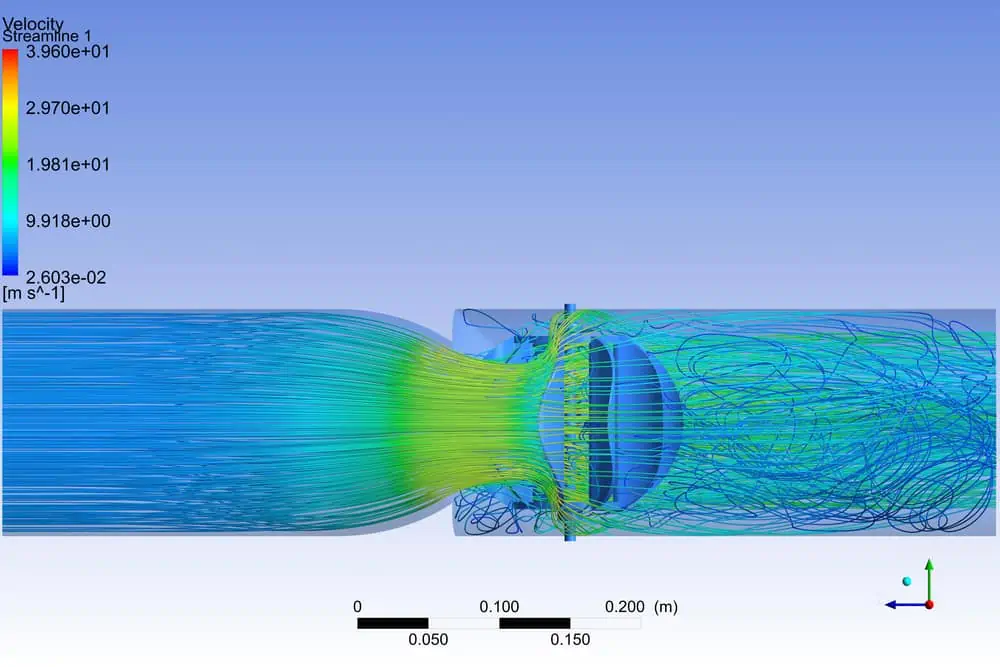
Pipe Flow Analysis
Engineers designing pipe systems have many important parameters to evaluate. Laminar and turbulent flow may not be the main problem they’re solving, but the type of flow still makes a difference.
The friction factor for laminar flow in a pipe is calculated using the Reynolds number and the only variables are fluid velocity and pipe diameter. However, calculating the friction factor for turbulent flow requires both the Reynolds number and the surface roughness of the pipe. The first step is to calculate the Reynolds number and determine the type of flow, then plug the Reynolds number into the appropriate equation and find the friction factor. The friction factor is then used to calculate other parameters like flow rate, pressure drop/head loss, and the power requirements for a pump.
Heat Transfer
Mechanisms designed for heat transfer are heavily dependent on turbulent flow. Convection calculations use a unitless value called the heat transfer coefficient, which is a numerical representation of how efficiently heat transfers from a flowing fluid to the surface around it. The heat transfer coefficient is proportional to the Reynolds number so the coefficient increases as the Reynolds number increases. Therefore, turbulent flow has a greater heat transfer coefficient than laminar flow and transfers heat much faster and more efficiently.
Turbulent flow is utilized in many forced convection systems such as heat exchangers, air conditioners, and fans, as well as natural convection phenomena like a breeze or tectonic plates that rely solely on buoyancy and gravity.
