Water is a vital substance used in various applications, including cooking, manufacturing, energy generation, and hydronic systems. Especially in water applications that involve heating, the boiling point of water is an important property that plays a crucial role in determining its behavior with respect to the surrounding environment. This article discusses the boiling point of water and how it varies with respect to pressure.

Water Boiling Point at Different Pressures
The boiling point of water is the temperature at which the pressure exerted by the vapor equals the pressure of the surrounding environment. As temperature increases, the movement of the water molecules also increases with the vapor pressure. At the boiling point, the liquid water molecules have reached enough thermal energy to overcome the intermolecular forces that hold them together in the liquid state, allowing the water to transform into gas.
Therefore, the boiling point of water changes depending on the pressure of the surrounding environment. At sea level where the atmospheric pressure is equal to 101.3 kPa (14.7 psi), the boiling point of water is at 100°C (212°F). This is called the normal boiling point.
However, as the pressure decreases, the boiling point of water also decreases, and vice versa. This means that water will boil at a lower temperature when the pressure is low, and it will boil at a higher temperature when the pressure is high.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.

This behavior is utilized in various industrial applications. For example, in vacuum distillation, low pressure is used to boil and separate volatile substances from non-volatile substances. On the other hand, in steam power plants, high pressure is used in the production of steam for electricity generation.
Calculating the Boiling Point of Water at Different Pressures
The boiling point of water is governed by the Clausius-Clapeyron equation — a fundamental equation that relates the vapor pressure of a substance with its temperature and specific latent heat, specifically at the transition region between two of its phases.
There are many forms to this equation. However, its usual form when used to obtain the boiling point of a substance at a given pressure is as follows:
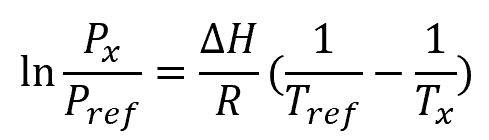
Where:
- Tx = unknown boiling point [K]
- Px = absolute pressure of the unknown boiling point [Pa, atm, or mmHg]
- Tref = known reference boiling point [K]
- Pref = absolute pressure of reference boiling point [Pa, atm, or mmHg]
- ΔH = latent heat of vaporization [J/mol]
- R = gas constant [J/K-mol]
The gas constant is equal to 8.3145 J/K-mol and, for water, the latent heat of vaporization is equal to 40.8 kJ/mol.
Note that this form of Clausius-Clapeyron equation assumes that vapor follows ideal gas law and that the liquid volume is much smaller than the vapor volume.
Example 1: Boiling Point of Water at 2 atm
For example, using the Clausius-Clapeyron equation and the normal boiling point temperature as reference, the boiling point temperature of water at 2 atm can be obtained using the equation:
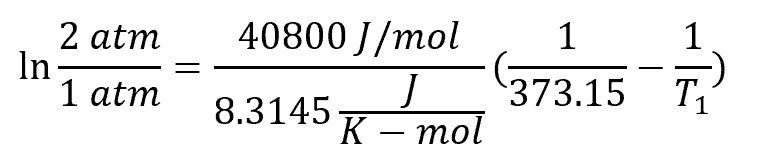
Where T1 is the water boiling point temperature at 2 atm, which equates to 393.15 K or 120°C.
Example 2: Boiling Point of Water at 20 psia
Using the same method, the boiling point temperature of water at 20 psia can be obtained using the equation:
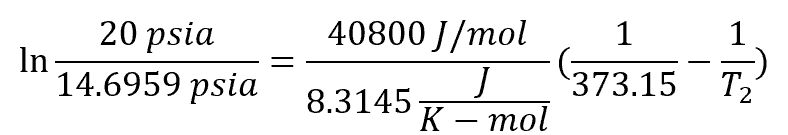
Where T2 is the water boiling point temperature at 20 psi, which equates to 382.15 K or 109°C.
Water Boiling Point Temperature Curve
Based on the Clausius-Clapeyron equation, the relationship between the boiling point temperature and the vapor pressure of water is not linear, instead, it is logarithmic. The diagram below shows how the boiling point of water changes with respect to pressure.
In the phase diagram of water, this represents the boiling curve connecting the triple point and the critical point, right between the liquid water and the water vapor regions.

Boiling Point of Water at Different Altitudes
Since the boiling point temperature is dependent on the surrounding pressure, it follows that it also changes with altitude. As altitude increases, the atmospheric pressure decreases; as a result, the boiling point of water also decreases. This is the reason why water boils faster in mountainous regions than on the sea level.
To calculate the boiling point temperature of water at a specific elevation, the first step is to estimate the pressure at that level and then use the Clausius-Clapeyron equation to obtain the corresponding boiling point temperature.
The common assumption is that the atmospheric pressure decreases by approximately 1 atm per 1000 feet of elevation. However, as shown in the diagram and table below, the atmospheric pressure varies non-linearly with altitude. The atmospheric pressure ranges from 101 kPa at sea level to almost 0 kPa at 30,000 meters.
Atmospheric Pressure vs. Elevation Chart
Atmospheric Pressure vs. Elevation Table
Atmospheric Pressure vs. Elevation Equation: Barometric Formula
The following formula can be used to estimate the atmospheric pressure at a given altitude:

Where:
- Pf = atmospheric pressure at the given altitude [Pa]
- Po = atmospheric pressure at sea level [101325 Pa]
- g = Earth’s gravitational acceleration [9.81 m/s2]
- h = altitude [m]
- M = molar mass of dry air [0.029 kg/mol]
- To = standard temperature at sea level [288.16 K]
- Ro = universal gas constant [8.314 J/mol-K]
The formula above assumes that temperature is constant and so it is only an approximation.
Boiling Point vs. Altitude Estimation
Alternatively, the following formula can be used to directly estimate the boiling point of water at a given altitude:
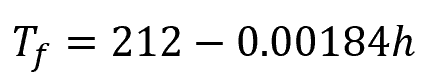
Where:
- Tf = water boiling point temperature in Fahrenheit [°F]
- h = altitude [ft]
Note that this formula is only an approximation based on standard conditions. It may not be accurate at very high altitudes or in cases where atmospheric pressure varies significantly from standard conditions.
