A pendulum is a rigid body suspended from a fixed point that swings back and forth. As it oscillates, it converts kinetic energy to potential energy and vice versa.

In this article, the different types of pendulums are discussed as well as their uses in various fields such as physics, engineering, and horology.
Basic Types of Pendulums
A pendulum is a body that hangs from a fixed point and swings back and forth when pulled and released. The word “pendulum” comes from the Latin word “pendulus,” meaning “hanging.” This principle of oscillatory motion was discovered by Galileo Galilei.
Depending on the configuration and the set of forces acting on the body, pendulums can be classified into three main categories: simple, compound, and torsional.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
Simple Pendulum
A simple pendulum is the most basic form of a pendulum. It consists of a point mass hanging from a string connected to a fixed pivot point. The string is assumed to be massless, hence, the only forces acting on the mass are the forces of gravity and tension, as shown in the diagram below.

The equations of motion for the pendulum can be obtained using Newton’s second law. In general, the period of oscillation, or the time it takes for a back-and-forth swing, of a simple pendulum can be approximated using the formula:
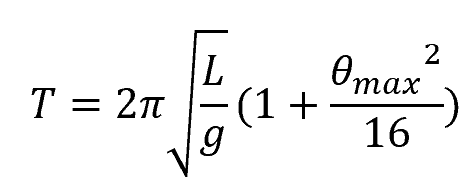
Where:
- T = period of oscillation [s]
- L = length of the string [m]
- g = acceleration due to gravity [m/s2]
- θmax = maximum amplitude [rad]
For small amplitudes, such that sin θ ≈ θ, the formula for the period of oscillation becomes:
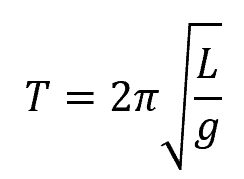
It’s worth noting that for small amplitudes, the period remains unchanged regardless of amplitude variations caused by factors such as friction or other disturbances. This feature is known as isochronism and is a critical element for time-keeping functions in clocks.
Compound Pendulum
A compound pendulum, also known as a physical pendulum, is any rigid object that can oscillate as a pendulum. However, unlike simple pendulums, a compound pendulum cannot be modeled as a point mass on a string. Hence, mass distribution must be considered when modeling the equations of motion.
In a compound pendulum, the force of gravity acts on the center of mass of the object. The effective length of the pendulum is, therefore, the distance between the pivot point and the center of mass, as shown in the diagram below.
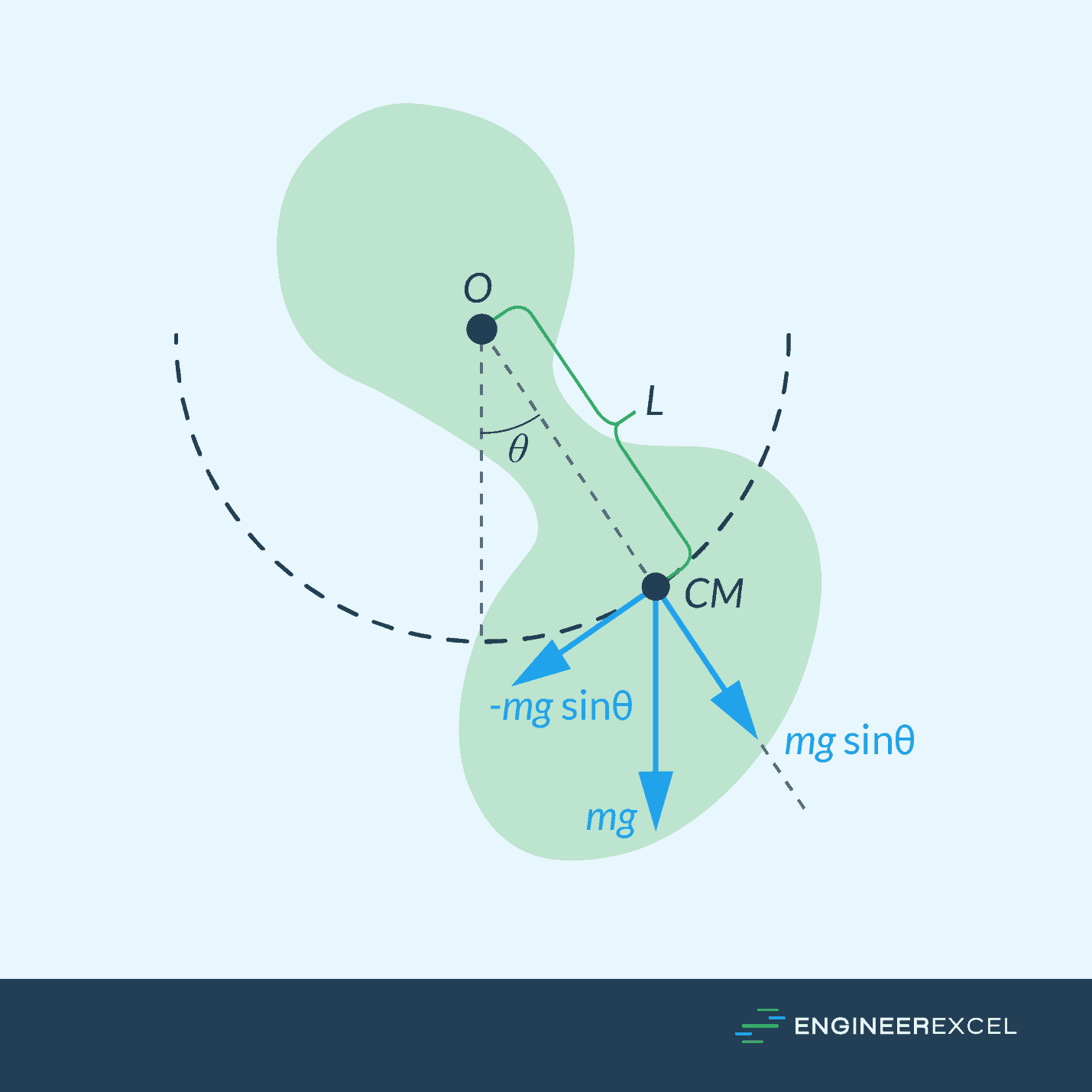
Using the conservation of angular momentum, the formula for the period of a compound pendulum becomes:
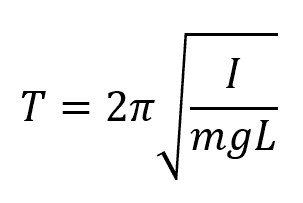
Where:
- I = moment of inertia of the object [kg-m2]
Torsional Pendulum
Rather than the swinging of a mass back and forth, as in the case of both simple and compound pendulums, the motion of a torsional pendulum is characterized by the twisting of a rod or wire suspended from a fixed point, as shown in the diagram below.
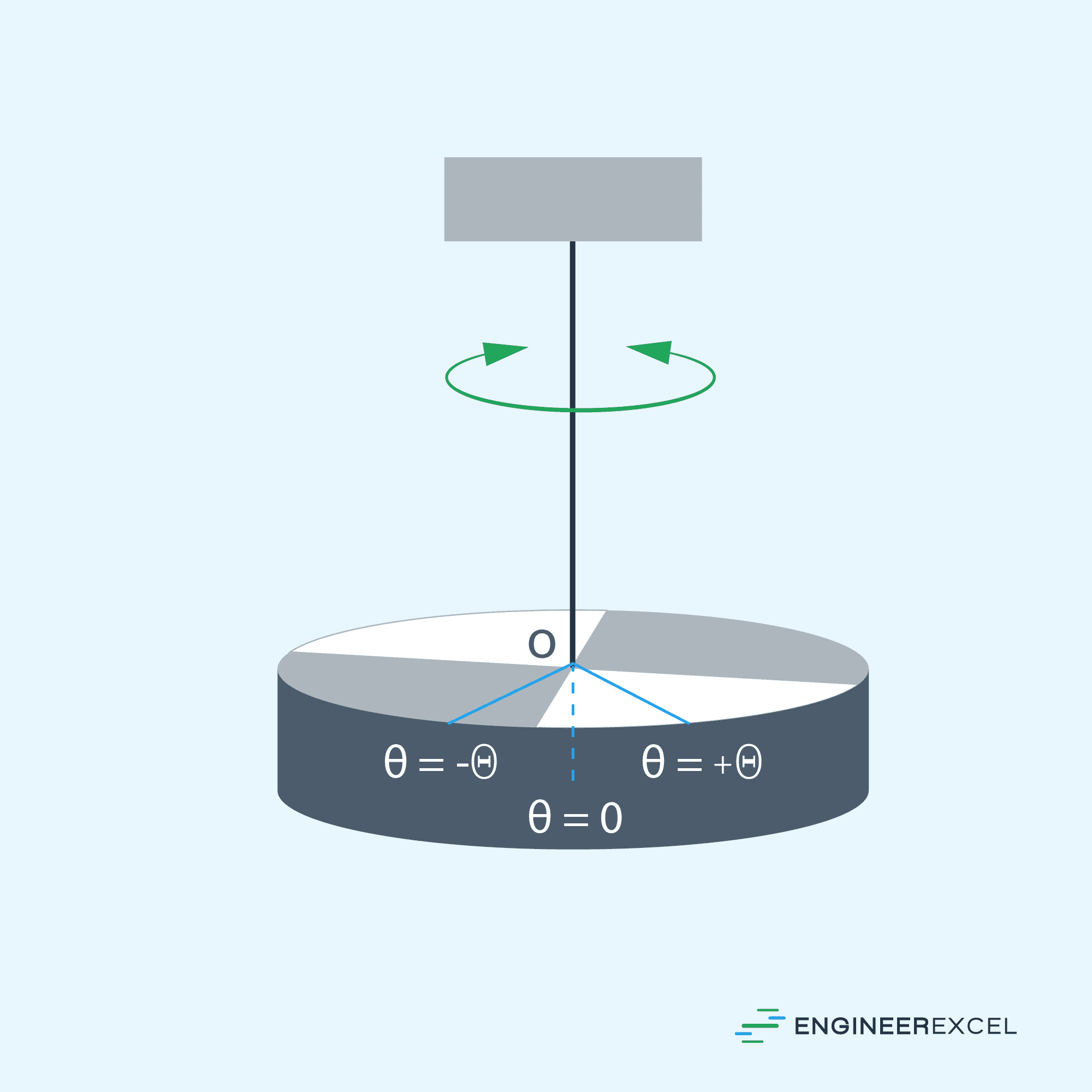
When the body is twisted to a certain maximum angle and released from rest, the body oscillates rotationally due to the restoring torque supplied by the shearing of the wire. The maximum restoring torque can be calculated using the formula:

Where:
- τ = restoring torque [N-m]
- κ = torsion constant of the wire or spring [N-m/rad]
Following this equation, the period of a torsional pendulum can be calculated using the formula:
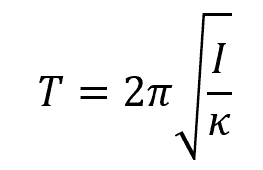
Special Types of Pendulums and Applications
Pendulums have been one of the earliest tools to be used for the measurement of time, gravity, pressure, and length. In this section, some of the special types of pendulums used in various applications are briefly discussed including the pendulum clocks, Foucault pendulum, seconds pendulum, Kater pendulum, and other pendulum gravimeters.
Pendulum Clocks
Pendulum clocks rely on the isochronism or regularity of pendulum swings to keep time. In the past, clocks were not precise, and people had to constantly adjust them with sundials. However, the introduction of the pendulum in the 16th century greatly improved accuracy.
In a pendulum clock, the movement of the pendulum controls the gears and levers that drive the clock’s hands. To fine-tune the clock’s accuracy, the clockmaker can adjust the length of the pendulum or the weight of the bob at the bottom. This ensures that the period of the pendulum matches the desired rate of timekeeping.
Foucault Pendulum
Jean Bernard Léon Foucault demonstrated the Earth’s rotation using a device called the Foucault pendulum, shown below. This pendulum is free to swing in any direction and its plane of oscillation remains constant, regardless of the pivot’s motion.

Foucault originally suspended a 67-meter pendulum from the Panthéon in Paris and observed its plane of swing changing the orientation of its rotational axis 360° clockwise in about 32 hours, showing the Earth’s rotation. This was the first time the Earth’s rotation was demonstrated without celestial observations. The Coriolis effect causes the rotation of the pendulum, as the Earth rotates underneath it, causing objects to move in curved paths.
The Kater Pendulum
The Kater pendulum, invented by Henry Kater in 1818, is a reversible pendulum that precisely measures the localized acceleration due to gravity. It consists of a long, thin, rigid rod with two knife-edge pivot points and two adjustable masses positioned so that the period of swing is the same from either edge.
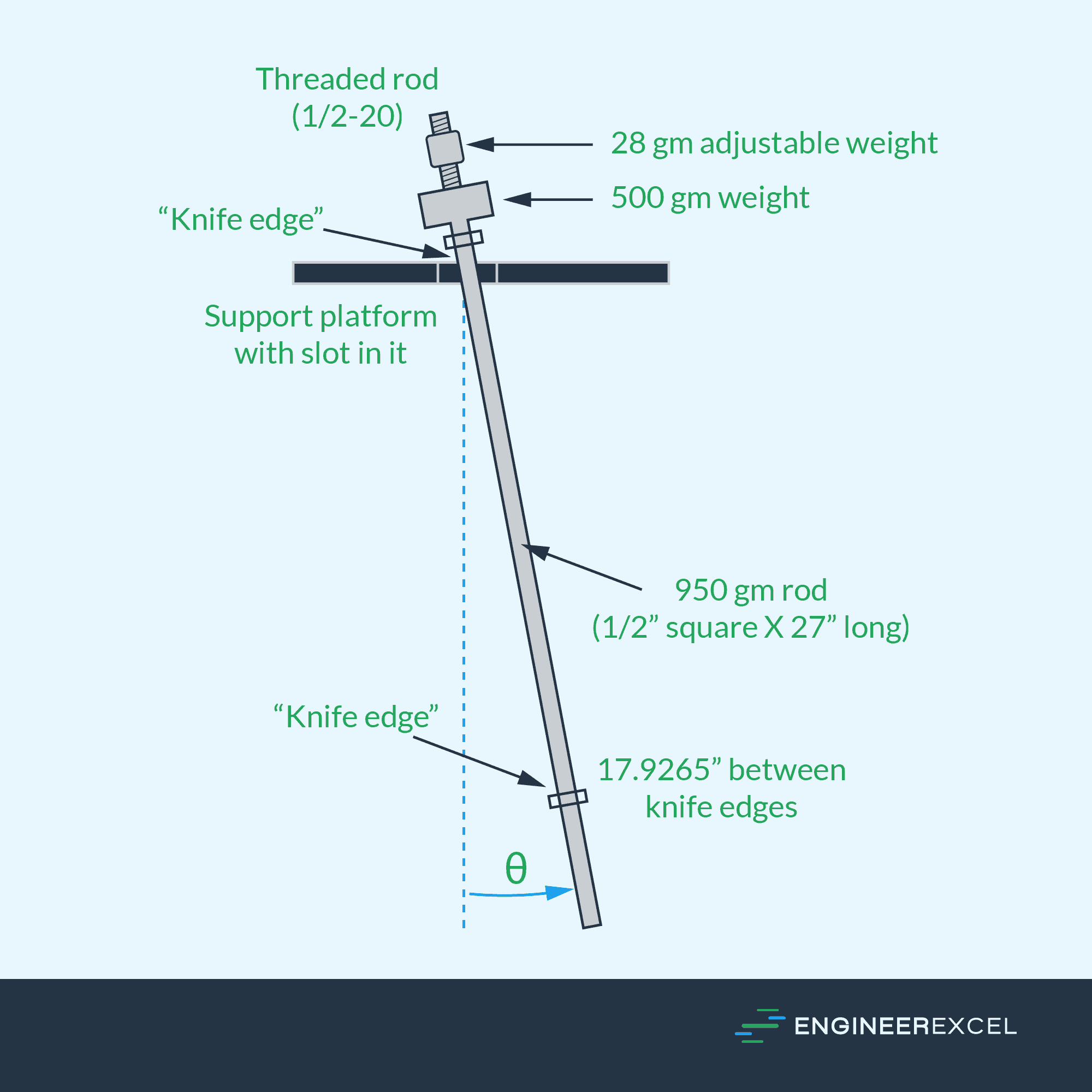
When the weights are in the correct positions, the pendulum will oscillate with a constant period regardless of the amplitude of the oscillation and the period will be the same as that of a simple pendulum whose length is the distance between the two knife edges.
By measuring both the length and the period of oscillation with great precision, the value of g can be determined using the formula:

The Schuler Pendulum
A Schuler pendulum is a type of pendulum that is designed to remain oriented along the local vertical direction of the earth’s gravitational field while the earth rotates.
Ideally, such pendulum should have a center of percussion at the earth’s center so that when the pendulum’s support is accelerated, the pendulum rotates in a way such that it always points towards the center of the earth. Although conceptually correct, the construction of such a pendulum is technologically impossible since it would require a distance between the support and the center of mass to be equal to 0.015 μm. This distance is in the atomic level and has never been constructed using purely mechanical means.
Currently, the Schuler pendulum is achieved by replacing the physical pendulum with a combination of gyroscope and accelerometers having the same dynamics. The period of a Schuler pendulum is given by:
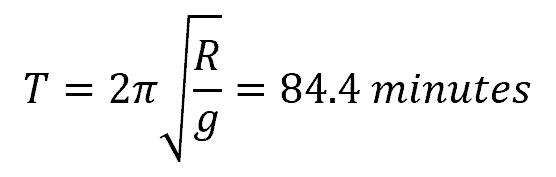
Where:
- R = radius of the earth [6370 km]
Note that 84.4 minutes is the same period as that of a circular orbit around the earth at zero altitude.
