Shock waves are sudden changes in pressure, temperature, and density that propagate through a medium at a speed higher than the local speed of sound. These phenomena are observed in various fields, such as aerospace and biomedical engineering, hence, it is important to accurately calculate shock wave parameters, especially in designing and optimizing engineering systems, like high-speed aircraft, hypersonic vehicles, and shock wave lithotripsy devices.
Shock Calculations
Shock calculations refer to the mathematical calculations involved in predicting the behavior of shock waves under different conditions, such as changes in fluid speed and temperature. These calculations have numerous applications, including the design and optimization of supersonic vehicles like aircraft and missiles, as well as providing insights into natural phenomena such as lightning and explosions. As such, shock calculations are an important area of research in fluid dynamics and aerospace engineering.

However, before learning more about shock calculations, it is important to understand the physics behind shock waves and how they form.
Understanding Shock Waves

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
Shock waves are sudden disturbances that occur when an object moves faster than the speed of sound. When an object or disturbance moves faster than the rate at which the surrounding fluid can transmit information, the fluid near the disturbance cannot react or move out of the way in time. Hence, the pressure front, moving at supersonic speeds, pushes on the surrounding air and creates a shock wave.
To demonstrate how a shock wave happens, consider an airplane as an example. As the airplane moves, it displaces the surrounding air and produces sound, which creates a series of circular wave crests emitted from the nose of the airplane.
Typically, when an airplane (source) moves slower than the speed of sound, the observed wave frequency approaching a stationary observer is given by the equation:
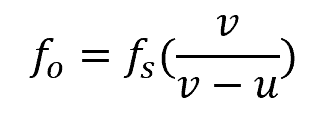
Where:
- fo = frequency observed by a stationary observer [Hz]
- fs = frequency measured at the source [Hz]
- v = speed of sound in the medium [m/s]
- u = speed of the moving source [m/s]
This equation shows that as the speed of the source increases, the observed frequency also increases. When the speed of the source reaches the speed of sound, the observed frequency approaches infinity, and all waves approach the observer simultaneously.
However, if the source exceeds the speed of sound, the observer will not hear any sound until after the source has passed. As the sound waves from the approaching source interfere with the receding sound waves, they mix together and create constructive interference along a conical front. This creates a disturbance known as a shock wave, as illustrated in the diagram below.
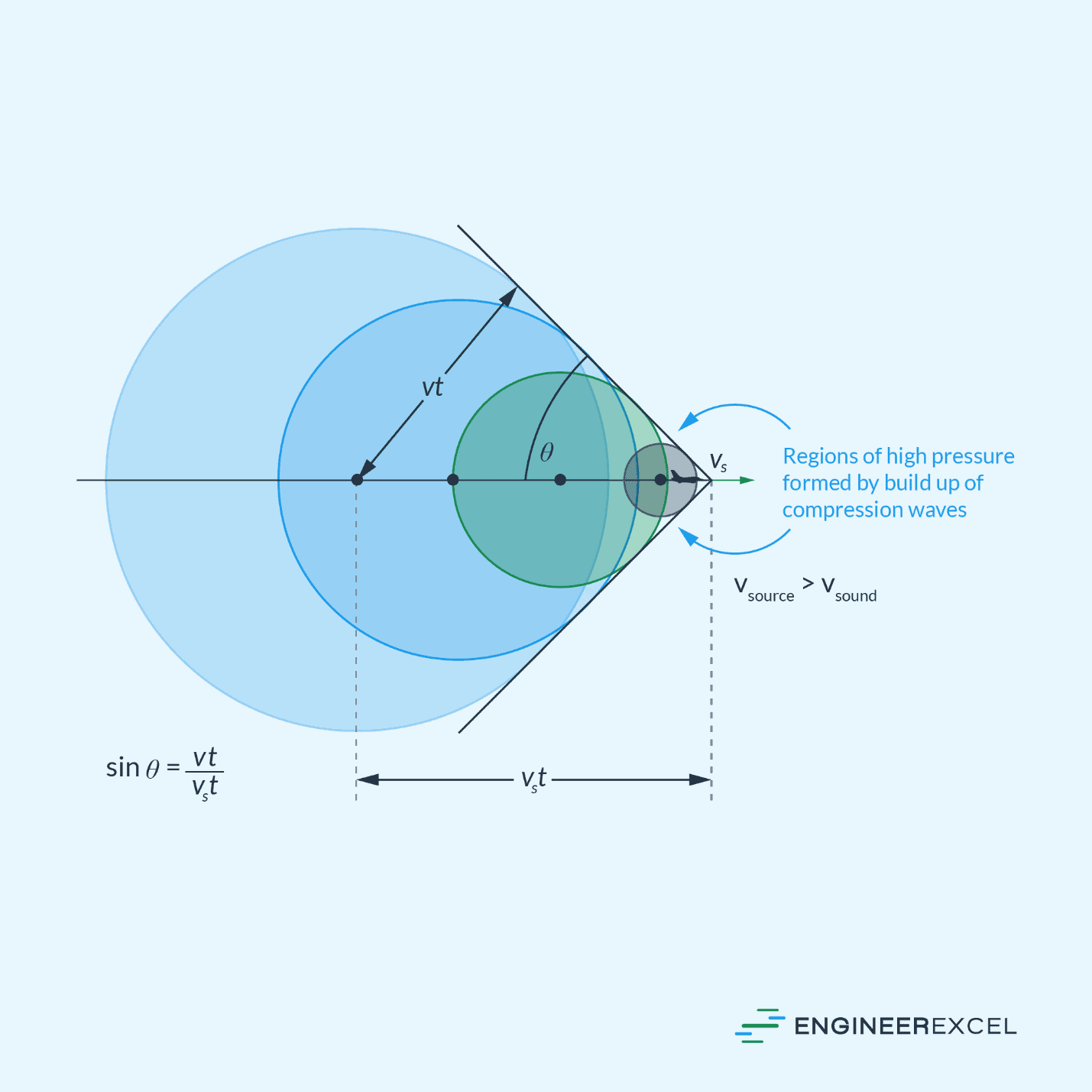
The conical line tangent to the circular waves represents a shock wave moving at an angle equal to:
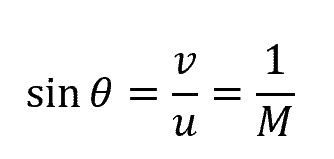
Where:
- θ = shock wave angle [degrees or radians]
- M = Mach number [unitless]
In general, a shock wave is a pressure driven compressive disturbance that produces irreversible change in fluid state— that is, increase of entropy.
Effect of Shock Waves
As shock waves propagate through a medium at supersonic speeds, they create abrupt changes in fluid properties, including pressure, temperature, and velocity. The pressure and temperature jump across a shock wave can be several times greater than the ambient conditions. Furthermore, shock waves create a region of high velocity gradients, which can cause shear forces and turbulence in the surrounding medium.
Shock waves can have a number of effects on the materials and objects they encounter. For example, a shock wave in air, which is usually created by the supersonic flight of an aircraft, can be heard as a loud noise known as a sonic boom.

Especially in low-altitude flights, sonic booms can cause structural damage, shatter glass and other brittle materials, and create intense heat and pressure that can ignite fires. Because of this, supersonic flights are banned over populated areas.
However, shock waves can also be used for beneficial purposes. In medical treatment, shock waves are used in a technique called shock wave therapy, where high-energy shock waves are directed at specific areas of the body to treat various medical conditions such as kidney stones, tendonitis, and plantar fasciitis.
In industrial applications, shock waves are utilized in ultrasonic cleaning— an eco-friendly cleaning process that uses high-frequency sound waves to efficiently clean delicate objects such as jewelry, medical instruments, and electronic equipment using less water and chemicals. The shock waves create microscopic bubbles in the cleaning solution, which then implode and create a shock wave that dislodges dirt and other contaminants.
It is important to note that, although shock waves are caused by constructive interference, the interference inside the conical region of a shock wave is mostly destructive, hence, the sound intensity there is much less than on the edge of the shock wave. Over longer distances, a shock wave can change from a nonlinear wave into a linear wave as it transfers heat into the air and loses energy.
Mathematical Models for Shock Waves
Shock wave calculations are based on the fundamental principles of thermodynamics, fluid mechanics, and gas dynamics. To calculate shock wave parameters, such as the shock wave angle, pressure ratio, temperature ratio, and density ratio, several mathematical models have been developed.
Rankine-Hugoniot Equations
One of the most widely used models is the Rankine-Hugoniot equations, which relate the shock wave properties before and after the shock wave passage. These equations are derived from the conservation laws of mass, momentum, and energy.
In general, the Rankine-Hugoniot jump conditions for a plane-parallel shock are as follows:

Where:
- ρ1, ρ2 = pre-shock and post-shock mass density of the fluid [kg/m3]
- u1, u2 = pre-shock and post-shock fluid velocity [m/s]
- P1, P2 = pre-shock and post-shock fluid pressure [Pa]
- ϵ1, ϵ2 = pre-shock and post-shock specific internal energy of the fluid [J/kg]
For a polytropic fluid, the third equation becomes:
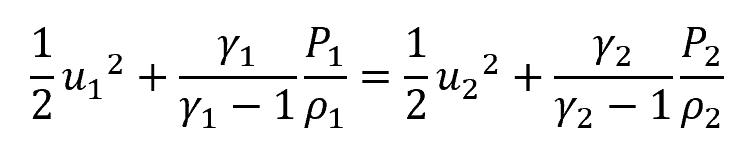
Where:
- γ1, γ2 = pre-shock and post-shock specific heat ratio [unitless]
It should be noted that in the case of oblique shocks, where the fluid enters the shock at an angle other than 90 degrees, the shock jump conditions apply only to the velocity component that is perpendicular to the shock. The parallel component of the velocity remains unchanged, resulting in the fluid being refracted by the shock, which alters its direction so that it becomes closer to parallel with the front.
Mach Number
The Mach number is a dimensionless quantity that characterizes the strength of a shock and is defined as the ratio of the speed of the fluid or an object to the local speed of sound in the medium. It is used to describe the behavior of supersonic flows and is an important parameter in aerodynamics. A strong shock wave is one that has a higher Mach number, while a weak shock wave has a lower Mach number.
Mathematically, the Mach number, M, is equal to:
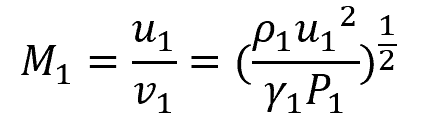
Note that the speed of sound in a medium depends on the temperature, adiabatic index, and molecular mass of the medium.
In terms of Mach number, the shock jump conditions can be written as:
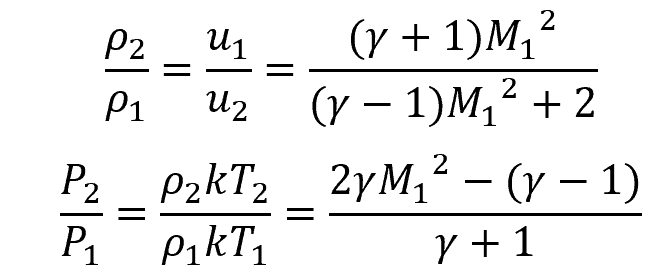
Numerical Hydrodynamics
Numerical hydrodynamics utilizes numerical methods to determine how shock waves affect the physical state of gas. The shock jump conditions, determined by conservation laws, establish the relationship between the physical properties of the gas before and after the shock.
To accomplish this, the method involves searching for areas where shocks are likely to occur and applying shock jump conditions within a specific scale. This technique is particularly beneficial for intricate shock wave geometries and unsteady flows observed in shock tube experiments and shock wave interactions.
An alternative approach, introduced by von Neumann and Richtmeyer, involves using an “artificial viscosity” significantly greater than the true viscosity calculated based on the microscopic properties of the gas. Despite the artificial viscosity, the shock jump conditions still adhere to conservation laws, ensuring the accurate relation between the pre- and post-shock gas properties.
Numerical hydrodynamics is a powerful tool for predicting shock wave behavior and providing insights into fluid flow physics. However, it requires careful consideration of the initial conditions, choice of numerical method, and validation of the results against experimental data or analytical solutions.
