Miles’ equation was originally developed by John W. Miles in 1954 to assist him in modeling the structural fatigue of aircraft using only one degree of freedom. The general form of the equation is:

where GRMS is the root mean square acceleration, measured in G’s, fn is the natural frequency, Q is the amplification factor at fn, defined by
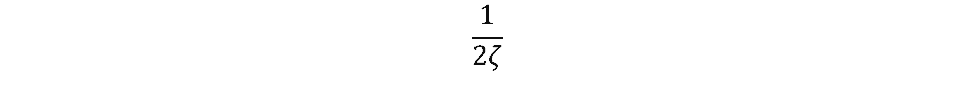
where ζ is the critical damping ratio, and [ASDinput] is the input acceleration spectral density at fn with units of g2/Hz.
The equation is derived as a lightly-damped single degree of freedom system consisting of a mass, spring, and damper. A constant random vibration in Hz is applied to the system from a minimum to a maximum value, and the resulting output can be used to determine the maximum load in response to vibration. This maximum load is then utilized for design calculations, reducing the number of calculations from many to one.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
Since its original development, Miles’ equation has been rearranged to be applied to displacements, forces, accelerations, and other calculations.
Miles’ Equation Example
During the design of a part, the first step to applying Miles’ equation is to calculate the resonant frequency of the part. This value may be determined through analysis such as finite element analysis. The calculated frequency is input into Miles’ equation as fn.
In the standard form of the equation, the result will be the load due to random vibration. Multiplying the result by 3 provides a 3-sigma load, which is a conservative value often used in the design of parts.
Oftentimes, during the design of a part, the ASD vs frequency will be calculated or provided by specifications. Using that information and either a specified or assumed value for the amplification factor, the vibration response spectrum can be calculated for various values.
For example, if several values of ASD vs frequency are given, a linear interpolation of that data can be used to determine the range of ASD and frequency values between the minimum and maximum values provided. Those values and the amplification factor are input to Miles’ equation to determine the acceleration response in G’s for random vibrations.
Based on the resulting accelerations, the maximum response can be determined and used for further analysis. By only using the maximum load at a particular frequency, it is only necessary to design a part for that load, which greatly reduces the number of calculations needed to ensure the part will be able to withstand the vibration environment.
How to Use Miles’ Equation to Calculate Displacement
When using Miles’ equation to calculate the displacement of a part, the equation is rearranged as follows:

In this application, the units of [ASDinput] are [length/s2]2/Hz, which allows for the resulting displacement in units of length.
The resulting output provides the displacement in the Y-direction for the part in response to the load resulting from the vibration frequency fn. Using the same process as outlined in the previous example, a plot can be generated that will highlight the largest displacement, to which the part should be designed. Again, the 3-sigma value is often used as a conservative value.
How to Use Miles’ Equation to Calculate Stress
Using the displacement calculated with Miles’ equation, the strain can be calculated as follows:
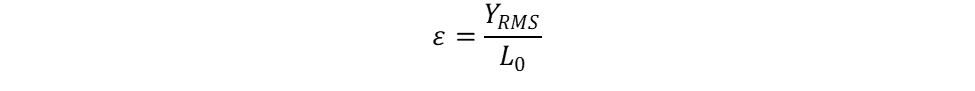
where L0 is the initial length of the part.
Taking the calculated strain, the stress can be determined using the following:
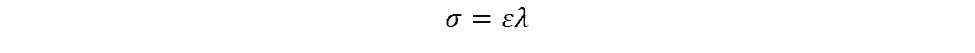
where λ is the elastic modulus of the part.
The stress calculation using Miles’ equation can be used to estimate the stress response of a part in response to a load caused by random vibration. Plotting the stress response in terms of various frequencies, the maximum value can be determined and used as the design value to minimize the number of calculations.
