Excel features many of the common mathematical functions that you’ll encounter in engineering: logarithms, exponentials, square roots and factorials.
This section covers three example problems that use these functions. Worksheet 03f is set up to calculate true strain from engineering strain data collected on a tensile test machine. The equation for true strain is:

where is the engineering strain found in column B. Select the first cell in the true strain column and enter the formula =LN(1+B5). Press Enter, select that cell
and double-click the fill handle to apply the formula to the rest of the column. This will allow you to see how the true stress and strain compare to the engineering stress and strain.
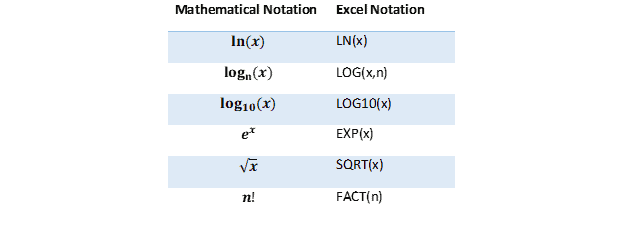
Logarithms come up often when dealing with sound measurements. For instance, a logarithm is used to calculate the overall sound pressure from sound measurements at individual frequencies. In Worksheet 03g, the A-weighted sound pressure level can be calculated from measured sound levels using the equation:

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
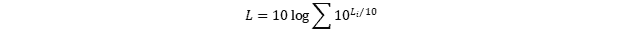
First, you’ll have to calculate ![]() from the corrected sound value, Li, in column E. Enter =10^(E4/10) in the first cell of column F. Select the first cell and double-click the fill handle. Next, we’ll calculate L using the SUM function to get the sum of the values in column F. In the large cell next to “Sound Pressure,” enter =10*LOG(SUM(F4:F11)). The LOG function assumes base ten unless you specify the base in a second argument, i.e. LOG(8,2) will find .
from the corrected sound value, Li, in column E. Enter =10^(E4/10) in the first cell of column F. Select the first cell and double-click the fill handle. Next, we’ll calculate L using the SUM function to get the sum of the values in column F. In the large cell next to “Sound Pressure,” enter =10*LOG(SUM(F4:F11)). The LOG function assumes base ten unless you specify the base in a second argument, i.e. LOG(8,2) will find .
Worksheet 03h contains an example using the exponential function. This function is used often for decaying oscillations. The ratio of successive oscillation amplitudes can be calculated if the damping ratio is known using the formula:
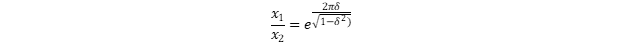
where x1 is the first oscillation amplitude, x2 is the second oscillation amplitude, and δ is the damping ratio. Worksheet 03h contains the first oscillation amplitude in cell C4 and the damping ratio in cell C5, so we can rearrange the equation to solve for the second oscillation amplitude. In the cell next to “Second Oscillation Amplitude,” enter =C4/EXP((2*PI()*C5)/SQRT(1-C5^2)).
Note that we’ve used three Excel functions here: EXP for the exponential, PI() for the value of π, and SQRT for the square root. Enclosing the exponent’s numerator and denominator in parentheses helps ensure Excel reads our formula correctly – this is a good habit to adopt.
