The partial pressure of a gas is the pressure that a single gas species exerts in a mixture of gases. It is a crucial concept in thermodynamics because it helps us understand the behavior of gases in a mixture and is a key factor in predicting gas reactions, determining reaction rates, and understanding gas transport. Learn how to calculate partial pressure below.
Finding Partial Pressure
The pressure inside a gas container is caused by the molecules colliding with the container walls and exerting a force whose magnitude depends on the average velocity of the molecules as well as the number of molecules per unit volume of the container. Hence, it is a strong function of the density and the temperature of the gas.

However, in a mixture of gases, there exists a relationship between the composition of the gas and its total pressure, which is defined by Dalton’s Law of Partial Pressures.
This law is based on two main principles. Firstly, in a gas mixture, each gas species has a partial pressure that is equivalent to the pressure it would exert if it were the only gas present. Secondly, the total pressure of the mixture is equal to the sum of all the partial pressures of the gas components.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
The value of the partial pressure of a particular gas species is proportional to its mole fraction. In simpler terms, the more of a specific gas there is in a mixture, the higher its contribution to the total pressure of the mixture.
Mathematically, this can be expressed as:
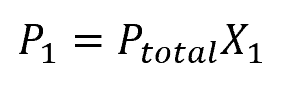
Where:
- P1 = partial pressure of a particular gas species [atm]
- Ptotal = total pressure of the gas mixture [atm]
- X1 = mole fraction of the gas species [unitless]
Note that, assuming ideal gas, this partial pressure is also equal to:

Where:
- n1 = total number of moles of the gas species [mol]
- R = universal gas constant [0.0821 L-atm/mol-K]
- T = absolute temperature of the gas [K]
- V = volume of the container [m3]
Based on the Dalton’s Law of Partial Pressures, it follows that the total gas pressure can be expressed as:
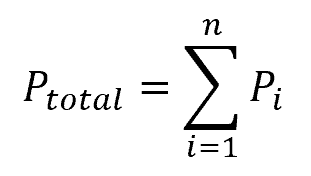
Where:
- Pi = partial pressure of each gas species [atm]
- n = number of gas species present in the mixture [unitless]
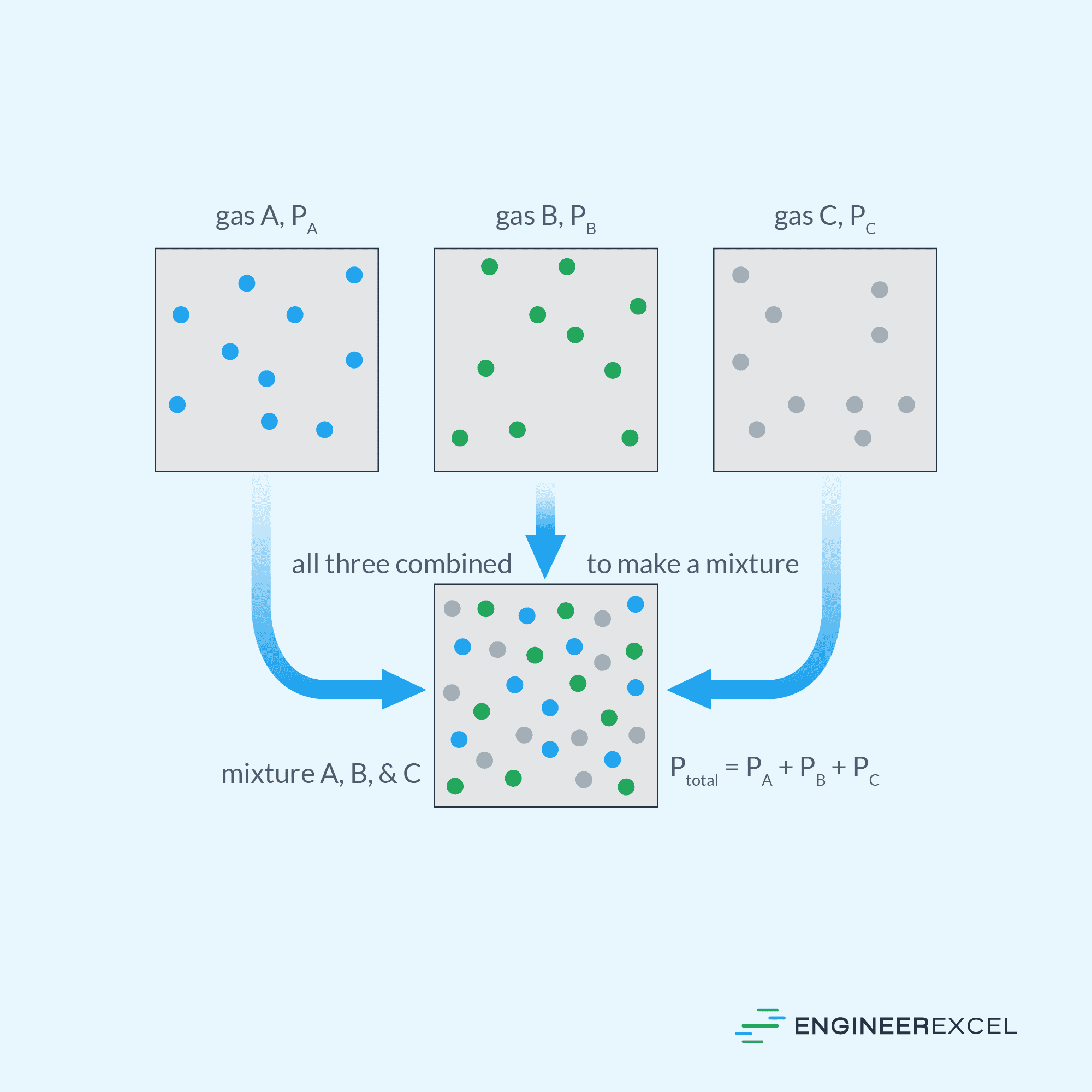
For example, as shown in the diagram below, gases A, B, and C with partial pressures PA, PB, and PC, respectively, combine to create a gas mixture with a total pressure equal to the sum of PA, PB, and PC.
Measuring Partial Pressure
Partial pressure is a theoretical concept that cannot be measured directly. As pressure arises from the collective impact of all gas molecules with the container walls, it is impossible to measure the pressure of specific molecules selectively. However, partial pressure can be indirectly calculated by its relationship with concentration or mole fraction.
Note that for an ideal-gas mixture, the mole fraction, pressure fraction, and volume fraction of a particular gas species are equivalent. Hence, the mole fraction can be obtained by performing volumetric analysis on the composition of the gas mixture.
This involves passing a gas sample with a known volume, pressure, and temperature into a vessel containing reagents that absorb one of the gases. The remaining gas volume is then measured at the original pressure and temperature, and the ratio of the volume reduction to the original volume represents the mole fraction of that specific gas.

From the mole fraction, Dalton’s Law of Partial Pressures can be used to calculate for the partial pressure.
Example Calculations of Partial Pressure
Example 1: Finding Partial Pressure Using Mole Fraction
To find the partial pressure of oxygen in a gas mixture that contains 0.3 moles of oxygen gas and 0.7 moles of nitrogen gas with a total pressure of 1 atm, do the following:
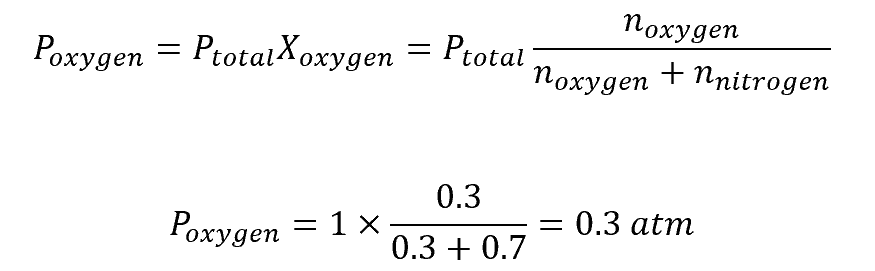
Example 2: Finding Partial Pressure Using Ideal Gas Law
To calculate the partial pressure of nitrogen gas in a 1.00 L sample of dry air at 290 K which contains 0.319 mol N2, 0.00856 mol O2, 0.000381 mol Ar, and 0.00002 mol CO2, do the following:
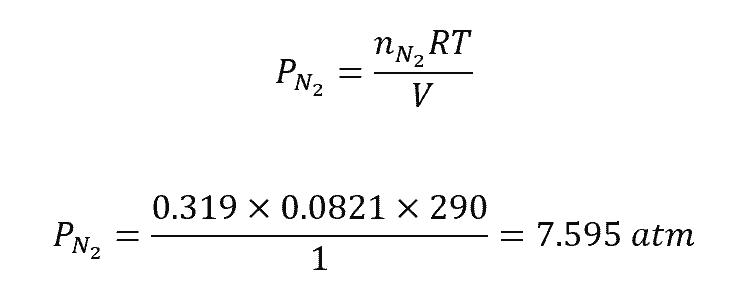
Importance of Finding the Partial Pressure
Partial pressures are a crucial concept in many engineering disciplines. The ability to determine the partial pressure of each gas species in a mixture allows for a more accurate understanding of the behavior of gas mixtures, which can be useful in various applications.
For example, finding the value of partial pressures makes it possible to accurately predict and optimize chemical reactions. This is because the partial pressure of each gas species affects the reaction rate and equilibrium constant.
Furthermore, in order to handle and store different gases safely, it’s important to consider the partial pressure of each gas species in storage tanks. This is particularly important in the storage of liquefied petroleum gas (LPG), where controlling the partial pressure of propane and butane is necessary to prevent explosions and fires.
In the field of atmospheric science, understanding the behavior of gases in the atmosphere is crucial, and partial pressures play a critical role in this. In fact, the atmospheric pressure can be considered as a combination of the partial pressures of air and water vapor, as depicted in the diagram below.
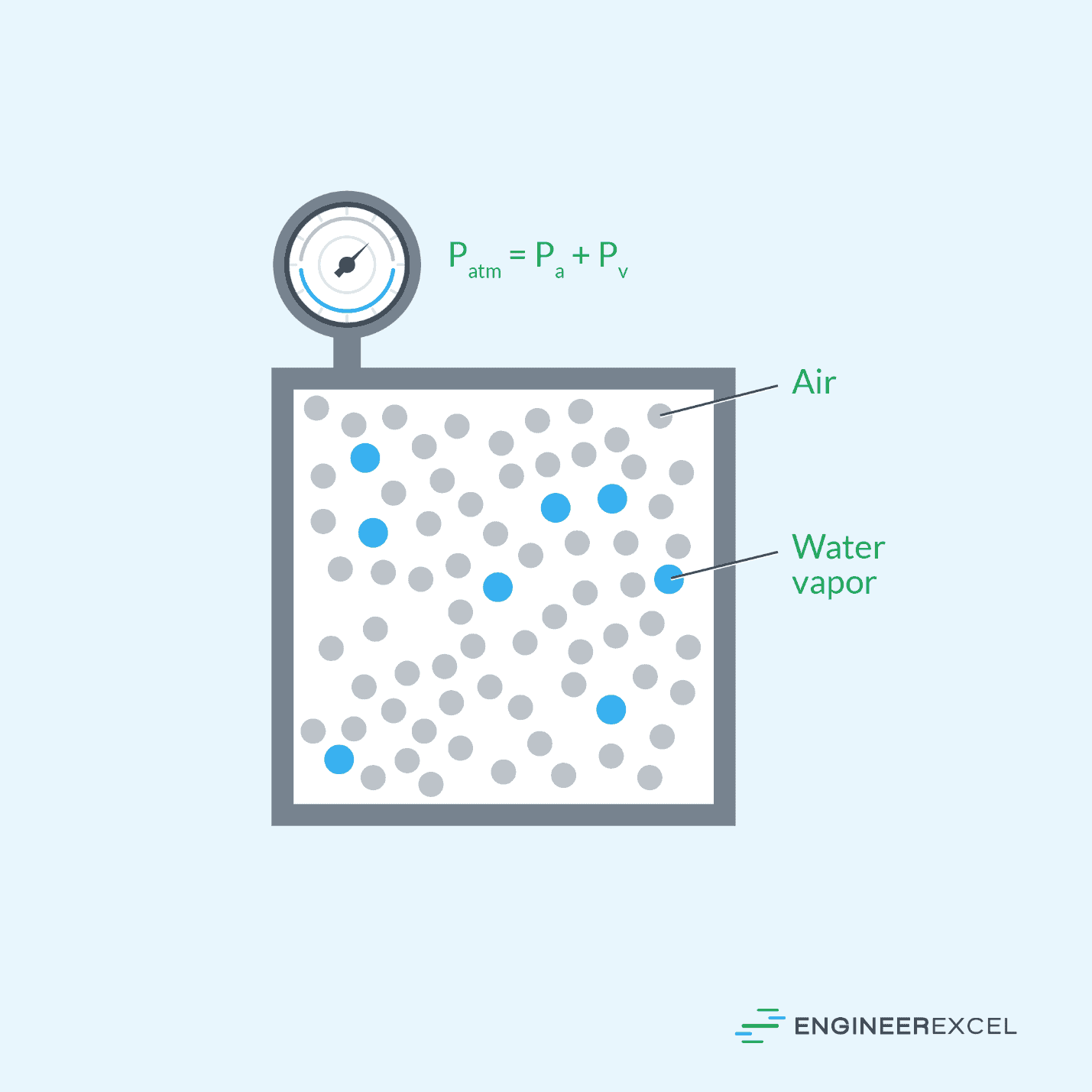
The partial pressure of gases in the atmosphere affects the atmospheric pressure, which, in turn, impacts weather and climate patterns. For example, changes in the partial pressure of carbon dioxide in the atmosphere can have a significant impact on global warming and climate change.
Lastly, in the field of medical science, the partial pressure of oxygen and carbon dioxide present in the bloodstream affects the respiratory system’s function and is a significant factor to consider when diagnosing and treating various medical conditions. For instance, during surgery, the partial pressure of oxygen is closely monitored to ensure that the patient receives the necessary amount of oxygen.
