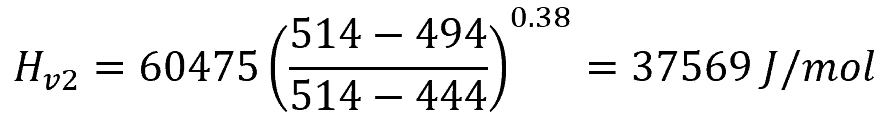The heat of vaporization is a fundamental property of a liquid which is used to evaluate how much energy is needed to convert the liquid to a vapor. The conversion of a liquid to a vapor is a function of the temperature and pressure, with a higher pressure requiring a higher heat of vaporization.

Definition And Importance Of The Heat Of Vaporization
The heat of vaporization, which may also be referred to as the enthalpy of vaporization, is the measure of how much heat (or thermal energy) is required to convert a given amount of liquid to vapor (gas). It can be thought of as the amount of energy to break the intermolecular bonds of the liquid, which is a chemical property of the liquid, therefore, different liquids will have different values.
The heat of vaporization can be calculated using the following formula:
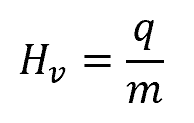

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
where:
- Hv is the heat of vaporization, with SI units of J/mol
- q is the heat (energy) applied to the liquid, with SI units of J
- m is the amount of the liquid, with SI units of mol
Therefore, for a given mass of liquid converted to a vapor, m, through the introduction of heat, q, the heat of vaporization can be determined.
Heat Of Vaporization And Boiling Point
The heat of vaporization is not the same as the boiling point of a liquid. The boiling point of a liquid is the point at which the vapor pressure is equal to the ambient pressure. As more of the liquid transitions to a vapor with increasing temperature, the vapor pressure will increase.

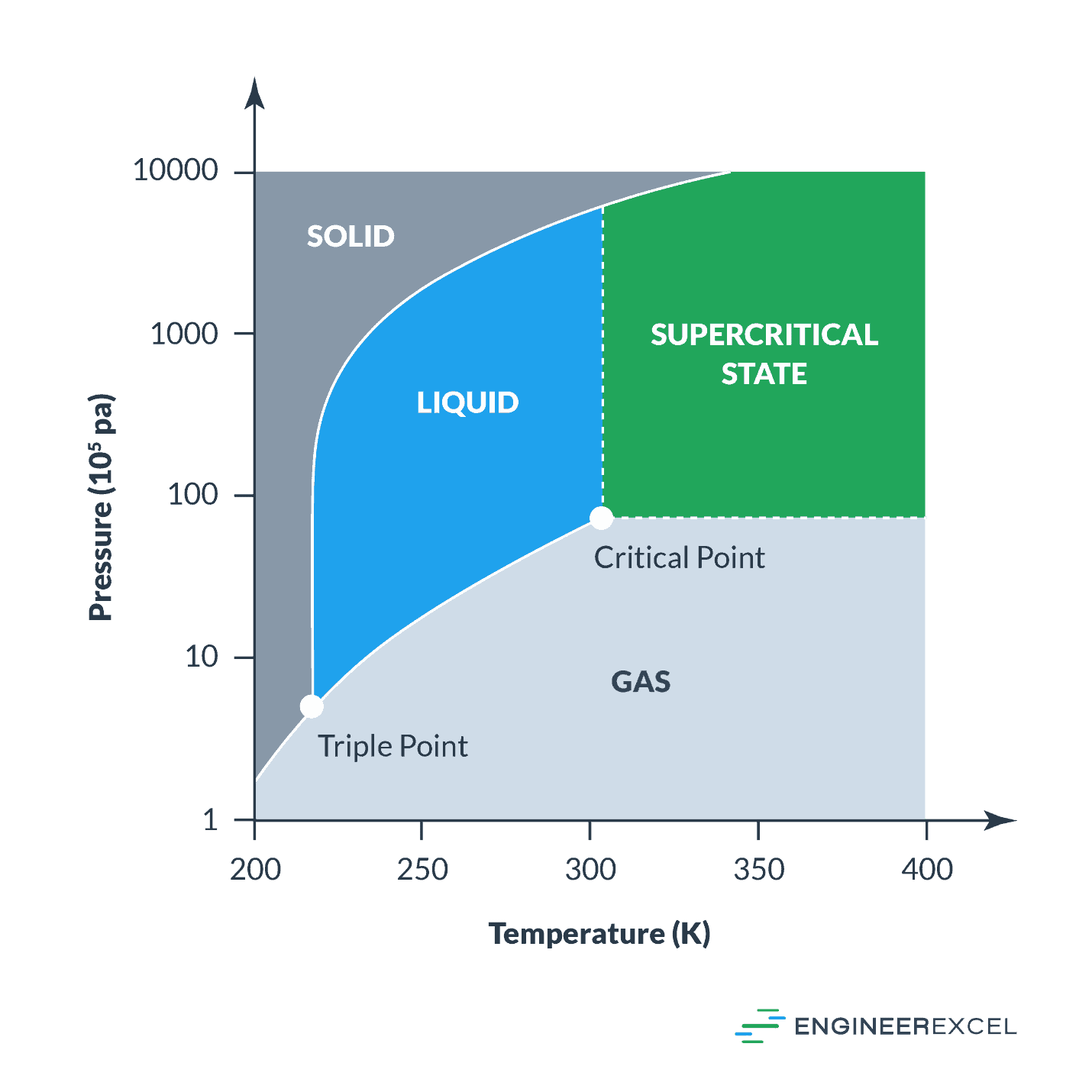
Critical Pressure And Temperature
The critical pressure of a substance is the pressure at which the substance is in the critical state. With regard to the heat of vaporization, the critical state is the point where the substance could be liquid and vapor at the same time. Likewise, the critical temperature is the temperature at which pressure alone cannot liquify the substance. The following image shows an example of various states of a compound:
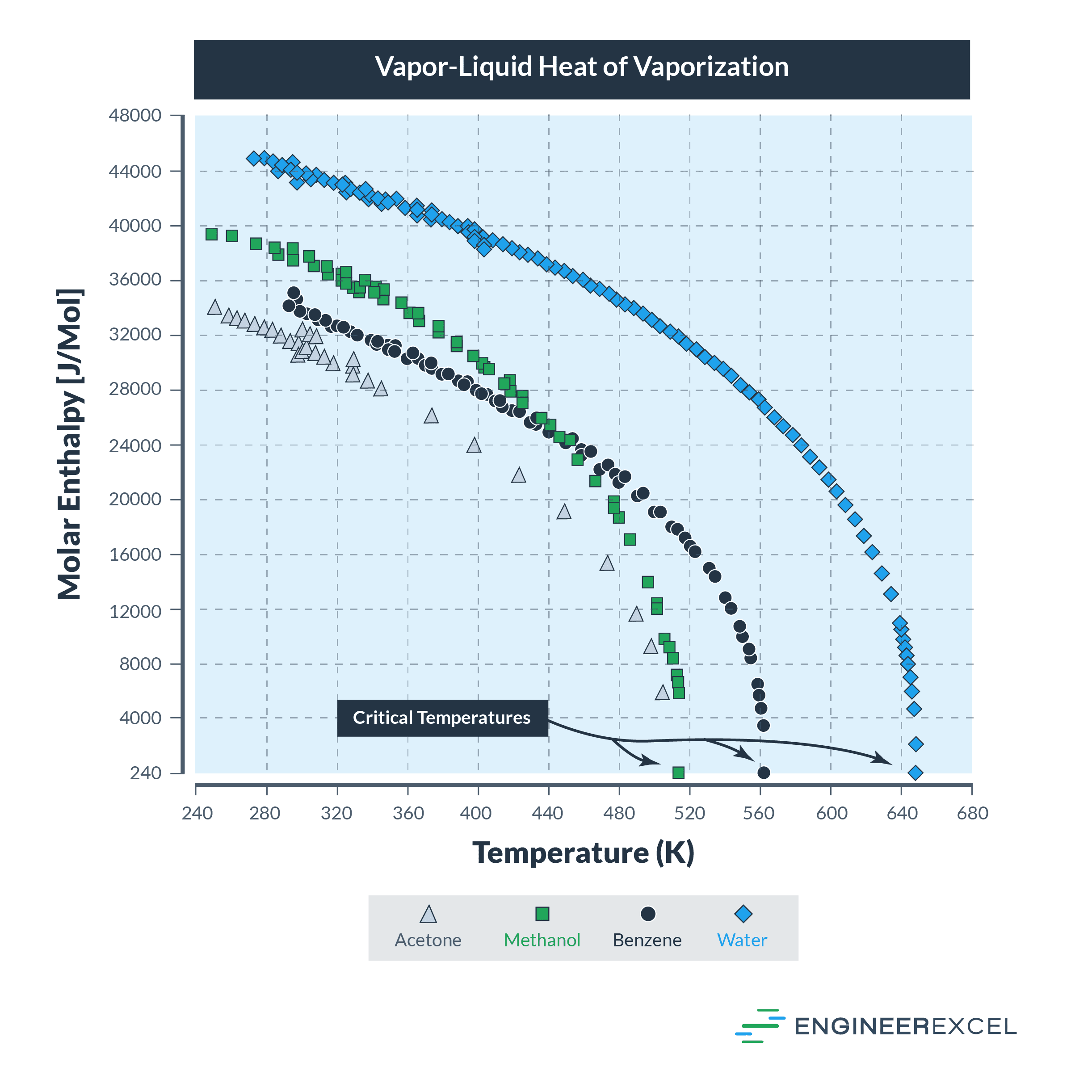
Temperature Variation
For some liquids, the heat of vaporization varies with the temperature. Examples of such liquids include acetone, benzene, and water. The following figure shows how Hv can vary with temperature:
Estimating The Heat Of Vaporization
The heat of vaporization can be calculated experimentally using the above equation. However, there are often scenarios where data cannot be obtained, either experimentally or otherwise, so the heat of vaporization under specific conditions can be estimated using one of the following methods.
The Clausius-Clapeyron Equation
For pure liquids (like water), the heat of vaporization can be estimated using the Clausius-Clapeyron equation, as follows:
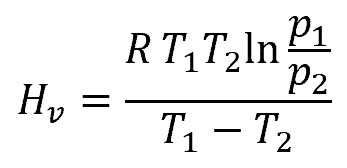
where:
- R is the gas constant, which is equal to 8.314 J/mol∙K
- p1 is the vapor pressure at T1, with units of atm
- p2 is the vapor pressure at T2, with units of atm
- T1 is the initial temperature, with units of Kelvin
- T2 is the final temperature, with units of Kelvin
Clausius-Clapeyron Assumptions
The use of the Clausius-Clapeyron equation for determining the heat of vaporization is subject to some assumptions, and is therefore not an exact value:
- The molar volume of the liquid phase is negligible compared to the molar volume of the vapor phase
- The vapor phase is considered an ideal gas
- The heat of vaporization is constant between T1 and T2
Example Calculation
For benzene, whose vapor pressure at 353 K is 1 atm and is 377 K at 2 atm, the heat of vaporization is calculated using the Clausius-Clapeyron equation as follows:
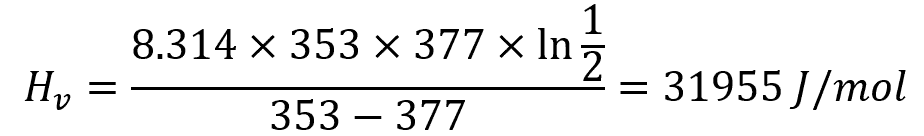
Riedel’s Equation
To estimate the heat of vaporization of a liquid at its normal boiling point, Riedel’s equation may be used:
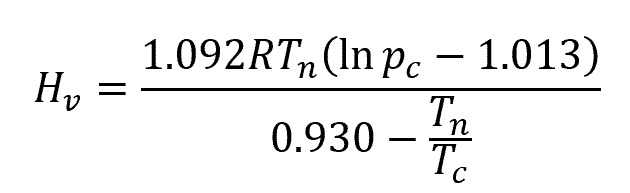
where:
- Tn is the normal boiling temperature, with units of Kelvin
- Tc is the critical temperature, with units of Kelvin
- pc is the critical pressure, with units of bar
For a given liquid, the values of Tn, Tc, and pc can be determined experimentally or using a lookup table. Riedel’s equation is considered a very accurate method for estimating the heat of vaporization.
Example Calculation
Again, using benzene as an example, with a normal boiling temperature of 353 K, a critical temperature of 562 K, and a critical pressure of 49.2 bar, Riedel’s equation can be used to calculate the heat of vaporization:
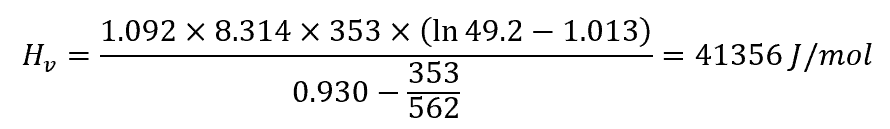
Touton’s Rule
Trouton’s rule relates the heat of vaporization and the normal boiling point of a liquid via the following ratio:
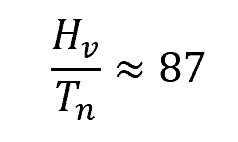
Using Touton’s rule will result in an estimate for the heat of vaporization, so it is considered a less accurate method.
Example Calculation
Using benzene as an example, the heat of vaporization can be estimated with Touton’s rule as follows:
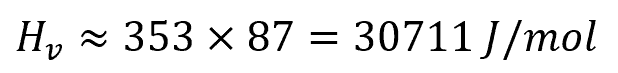
Watson’s Equation
If the heat of vaporization of a liquid is known at a given temperature, it can be estimated at another temperature through Watson’s equation:
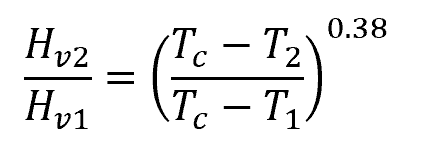
Example Calculation
For a liquid with a critical temperature of 514 K that has a heat of vaporization of 60475 J/mol at 444 K, the heat of vaporization at 494 K can be calculated as follows: